Prime Numbers

The Infinity of Primes

We present two proofs of one of the great theorems in number theory, namely that there are infinitely many primes.

Haris Angelidakis

Apr 13, 2020 — 7 min read

Famous Hungarian mathematician Paul Erdős (1913–1996) was known for many things, one of which is “The Book”. Although an agnostic atheist who doubted the existence of God (whom he called the “Supreme Fascist”, or in short, SF), Erdős often spoke of “The Book”, a visualization of a book in which God had written down the best and most elegant proofs for mathematical theorems. Lecturing in 1985 he said:

“I’m not qualified to say whether or not God exists. I kind of doubt He does. Nevertheless, I’m always saying that the SF has this transfinite Book that contains the best proofs of all mathematical theorems, proofs that are elegant and perfect…You don’t have to believe in God, but you should believe in the Book.”

— Paul Erdős —

[Source: https://en.wikipedia.org/wiki/Paul_Erd%C5%91s#cite_note-26]

In this article, we will discuss a theorem whose proof, gifted to us by Euclid, without a doubt deserves a chapter in this glorious “Book”. The statement of the theorem, which most of you have already heard, is the following:

Before proceeding with 2 proofs of the above theorem, it is worth noting that, as a tribute to Erdős, the mathematicians Martin Aigner and Günter M. Zieglerwrote an approximation of “The Book”, which they named “Proofs from THE BOOK”. It is a beautiful book, quite accessible, which I highly recommend.

The cover of the “Proofs from THE BOOK” by Martin Aigner and Günter M. Ziegler.

The material of this article is essentially based on the first chapter of their book. We will present 2 proofs, the first by Euclid and the second by Paul Erdős.

Euclid’s Proof of the Infinity of Primes

[UPDATE: The original version of this article presented Euclid’s proof as a proof by contradiction. The proof was correct, but did have a slightly unnecessary step. However, more importantly, it was a variant and not the exact proof that Euclid gave. This historical inaccuracy was pointed out to me by Michael Hardy; see the 1st response in this article. I would like to thank him for pointing out this historical error. The proof in this article has since been reworked. It is now a direct proof (and not by contradiction) and is much closer to Euclid’s original proof.]

Let’s assume that we are given a finite set P of distinct primes:

We now consider the following natural number m:

This number m has a prime divisor; let p be such a prime divisor of m. The key observation now is the following:

To see this, suppose that this is not the case. This means that p is a divisor of both m and of the product of all primes. More formally, we can then write that

where A and B are positive natural numbers that satisfy A > B. Taking the difference now, we get that

Note that the difference A-B is a positive natural number. Thus, for the above equation to hold, we must have that

Since we assumed that p is a prime divisor, we get a contradiction, and so we conclude that indeed the observation we made above holds, namely that

This means that p is a prime number that does not belong to the set P. Thus, any finite set of primes P can always be extended by adding a prime to it that is distinct from all the primes contained in P. We conclude that no finite set of primes can contain all prime numbers. The theorem is proved!

Erdős’s Proof of the Infinity of Primes

The proof by Erdős actually proves something significantly stronger, namely that if P is the set of all primes, then the following series diverges:

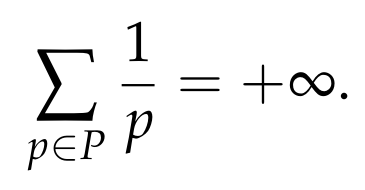
As a reminder, a series is called convergent if its sequence of partial sums has a limit L that is a real number. More formally,

If a series is not convergent, then it is called divergent. The first important observation here is that if a series is not convergent, then it must contain infinitely many non-zero terms. And this is what we will use in our proof. Note that the converse is not true in general; in particular, a series might contain infinitely many non-zero terms, but it can still converge (e.g., geometric series).

To recap, the proof plan is the following. We will consider the sum of reciprocals of prime numbers, and we will show that the sum is divergent. This will imply that the number of non-zero terms must be infinite, otherwise, the sum would have been finite. This further implies that there is an infinity of primes! And we will be done! Before proceeding, we should note here that the divergence of the sum of the reciprocals of prime numbers was first proved by Euler in 1737; see here for details. But the proof we will present was devised by Paul Erdős.

The proof will again be by contradiction. We define the sequence of the prime numbers in increasing order:

and let’s assume that the sum of their reciprocals converges to some positive real number L, which means that

If you are worried that by writing the above, we have implicitly assumed that primes are infinite (since the summation is infinite), then let me clarify that there is no issue whatsoever. We can actually define the sum as the sum of reciprocals of all primes, and then, if we run out of terms, just replace all “non-existent” terms with 0’s, such that the summation does not change. In other words, we slightly abuse notation and just use the infinite summation notation, even if the summation is actually finite.

We now use the definition of convergence of the sequence of partial sums. From the above conversation, we have

Since the sequence of partial sums converges, by using the formal definition of convergence (see here), we conclude that there exists a natural number k, such that

We now introduce the following terminology:

We now define N to be equal to:

We will consider all natural numbers from 1 to N, and split them into two groups as follows:

the numbers that are divisible by at least one big prime (suppose that there are N(b) many such numbers), and
the numbers that are only divisible by small primes (suppose that there are N(s) many such numbers).

Note that by definition, we have that N(b) + N(s) = N. We will now try to estimate N(b) and N(s).

We start with N(b). Note that we want to count all natural number from 1 to Nthat are divisible by at least one big prime. For any prime number p, the number of positive natural numbers smaller or equal to N that are multiples of p is at most N / p. Thus,

where the last inequality follows from the definition of k.

We now turn to N(s). We write every number n ≤ N that only has small prime divisors as follows:

Note that any natural number can be written is such a form; see here for details. This, in particular, implies that, since n only has small prime divisors, the term aₙ is just a product of distinct small primes. Since there are k many small primes, this means that there are 2ᵏ different square-free parts. Moreover, since n≤N, we get that