I had the pleasure of witnessing this interaction the other day: two kids were locked in a battle of wits to see who could think of the highest number.

Player one served with a million. Player two with an amazing return of a billion. Player one went for the smash: INFINITY. But player two caught it on the volley — INFINITY PLUS ONE.

At this point the umpire (me) intervenes with the ruling that infinity plus one is actually just infinity. (I ignored the technicality that if they are counting cardinals, then they should have said aleph null — they are just kids after all.)

How can this be? After all, at school they were taught that when you add a number to another number, you make it bigger. By that logic infinity plus one must be larger than infinity.

The problem with infinity is that it is larger than any (finite) number you can think of and it defies all intuition. Some interesting features of infinity are illustrated in a thought experiment presented by David Hilbert in 1924.

Hilbert’s Hotel

Every year there is a conference on hyper dimensional maths. The whole universe is invited and they all stay in Hilbert’s Hotel. Thankfully, this hotel has infinitely many rooms and (unlike any maths conference I have been to) all the rooms are booked up.

Problem 1

During dinner, a latecomer arrives. He rings the bell at the front desk and along comes a tired-looking bellhop.

“We’re full” the bellhop proclaims and slowly starts to trudge away.

The manager Hilbert immediately interrupts and asks the bellhop to get the person in room one to move all their stuff into room two. The occupant in room two then moves all their stuff to room three and so on and so forth. Since there are infinitely many rooms, this will not cause a problem since there will always be a next room to move into. This now frees up room one for the latecomer to move into.

Result!

What about if a (finite) group of latecomers arrive? Say three.

Using a similar method, Hilbert gets the bellhop to move the occupant of room one into room four (1+3), the occupant of room two moves into room five (2+3) and so on each person moving up by three rooms each time. This then frees up three rooms for our late party to move into.

So our tired bellhop (from having to move an infinite number of people one room up) can deal with any finite party coming into a full hotel.

Problem 2

Now in the middle of the night a SuperBus arrives. This bus is rather special since it contains an infinite number of people, all eager to get to their respective beds.

The bellhop gulps. The previous method definitely won’t work since he can’t move the occupant of room one into room ‘infinity plus one’. Let alone the occupant of room two and so on.

Apart from building a new hotel, the bellhop is all out of ideas. So he reluctantly wakes up Hilbert.

“We have a problem” he says sheepishly.

Still half asleep, Hilbert instructs the bellhop to move the guest in room one into room two, occupant of room two into room four, room three into room six. In general, the occupant of room n gets moved into room 2n. This frees up every odd room . Then everyone in the bus gets assigned a number m, then gets moved into room 2m-1, which is each odd number. Problem solved!

Problem 3

In the small hours of the morning, all hell breaks loose; an infinite hoard of SuperBusses arrive. Hilbert leaps into action, he had envisioned this event and already had a plan.

He assigns guest in room k to room number 2ᵏ. So the guest in room 5 gets moved to room 32.

He assigns every bus a prime number starting with 3 (there are infinitely many primes so this is fine) and then numbers each person in each bus. Then the kᵗʰ passenger in bus p gets assigned to room pᵏ. For example, the second passenger in the 11ᵗʰ bus gets sent to room 121.

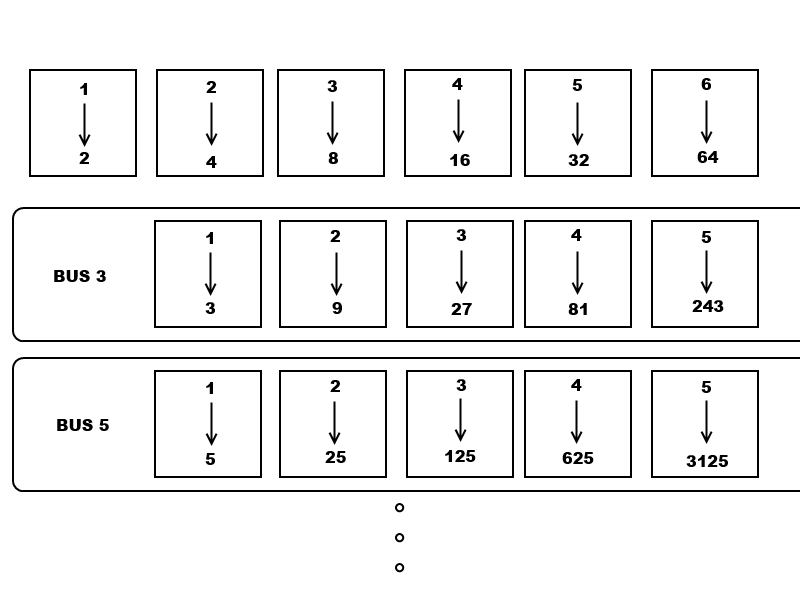
This method leaves lots of rooms empty but that’s fine since at least we got everyone in and ready for the conference.

Extension Problems

There are a few more problems that I will leave here for you to ponder over.

Suppose the hotel is next to an ocean and an infinite fleet MegaBoats arrive each carrying an infinite fleet of MegaBuses. How can they be accomodated?

This is three layers of infinity so to speak. Can you generalise to accomodate an arbitrary number of layers of infinite guests? How about infinitely many layers of infinite guests?

Infinity is a MESS

Infinity is so much bigger than we can understand: An infinite number of infinite number of infinite passengers. Little thought experiments like this one shows us that

1. Infinity is really large, like really really large
2. We really don’t understand infinity

It gets worse.

There are larger types of infinities and this is the smallest. The next highest infinity is mind-bogglingly larger than the one we have encountered in Hilbert’s Hotel. But for now, we will let the poor bellhop sleep for a bit.

*Unless otherwise stated, infinity will refer to countable infinity. This means there is a way ‘count’ up to it. It is the ‘last number’ in the list 1,2,3,4,…