Adding probabilities and velocities have at least two things in common — a maximum and Pascal’s triangle.

Introduction

Firstly, I know I will be disappointing some but reassuring others that this is not about Relativistic Quantum Mechanics. If you are comfortable with basic algebra, you should find it fairly easy to follow this article. If you’re already familiar with Pascal’s triangle, please skip the next section.

What is Pascal’s Triangle ?

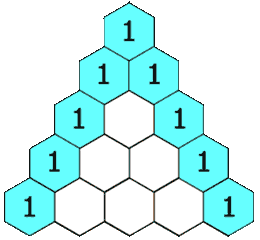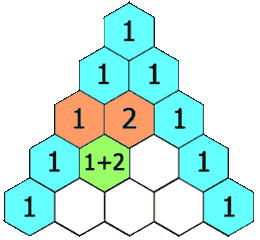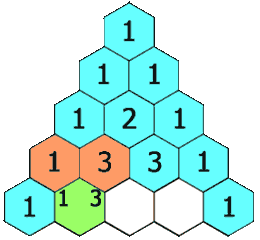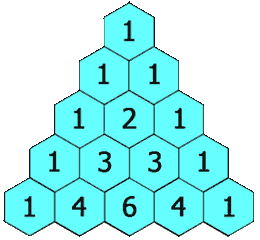
Pascal’s triangle is an pictorial algorithm for obtaining the coefficients for binomial expansions of various powers. For example the 3rd row counting from zero in the animation above, tells us that the binomial expansion of degree 3 is:

The next row in Pascal’s triangle is obtained from the row above by simply adding the values above-left and above-right of each cell. There is also a closed form to get coefficient for term k of the expansion of degree n. More efficient but less fun:

Pascal’s triangle pops up in all sorts of strange and interesting applications. Many different sequences can be derived from it and even patterns such as the Sierpinski Triangle fractal. But alas, we have to move on. I’ll just mention one property that we’ll need later: For any row n, the sum of the odd terms will equal the sum of the even terms.

Probability and Risk

I was whiling away an idle moment toting up micromorts when I went off on an unexpected but entertaining tangent.

So what is a micromort? From Wikipedia:

A micromort (from micro- and mortality) is a unit of risk defined as one-in-a-million chance of death. Micromorts can be used to measure riskiness of various day-to-day activities. A microprobability is a one-in-a million chance of some event; thus a micromort is the microprobability of death.

For example, a single skydive in the US or UK incurs about 8 micromorts. It feels as if doing 2 skydives is twice as risky as doing one- 16 micromorts. We’ve evolved an intuition that risks add which is indeed very close to the case for small risks. We never developed an instinct for how to combine large risks; instead we have a strong inclination to avoid them. Those who didn’t left far fewer descendants, so indulging in large risks is now fairly rare. Selection continues to improve this aversion as is attested to by the Darwin Awards. While we are interested in getting a payout, we are highly motivated to keep our risk low because we want to stay in the game as long as we can. This subject is covered in Chapter 6:“Hot Heads” of “How the Mind Works” by Steven Pinker.

In fact micromorts add as follows (which I’ll explain below):

So the risk of doing two skydives is actually 15.999936 micromorts. For all practical purposes micromorts combine with simple addition unless the numbers involved are a large fraction of a million.

But we were all taught to combine probabilities with multiplication in school, so which is actually the case? Sort of both as it turns out. We do combine probabilities with multiplication but we can only participate in the second event if we have already survived the Russian roulette of the first event. To avoid an ugly constant, let’s step away from micromorts and deal instead with probabilities where 1 represents certainty. The probability of survival is 1 minus the probability of death from an event, so we can define an operator for probability “addition” as follows:

We can get an intuitive understanding of this equation from the following diagram:

Here the total blue area (light and dark) is the probability of death. As long as pand q are small compared to 1 , p+q is very close to the correct answer. It is only out by the area of the overlap shown in dark blue.

We’ve defined an operation for adding probabilities. Moreover this operation is both commutative and associative. How about multiplication? Let’s start with multiplying by 2 which is simply adding a probability to itself. So setting q to pin Equation 5 we get:

To get the rule for multiplying by 3, we substitute the value for 2p in Equation 6 for q in Equation 5 and simplify to get:

The eagle eyed reader might notice that the last two equations have familiar coefficients giving us the general rule:

To multiply a probability by n:

Go to row n in Pascal’s triangle and throw away the initial 1.

Then read off the coefficients alternating between positive and negative as we go.

This is a consequence for the general result being a form of binomial:

This is the same form as equation 2 with x=1 and y = -p except that the constant 1 term has cancelled.

For want of a better terminology, let’s call this a reversible saturation arithmetic. Something that behaves like normal arithmetic for values ≪1 but cannot generate values > 1 i.e. it saturates at one. I’ve added the word reversible to distinguish it from a saturation arithmetic that just clamps its result to the maximum value. With a reversible arithmetic, after addition we can still recover one of our original operands by subtracting the other one from the result. This is true for a reversible saturation arithmetic provided our operands are both less than 1.

So is there another example of such an arithmetic? The one that immediately comes to mind is the relativistic addition of velocities in a universe where no velocity of anything can ever be observed exceed the speed of light.

Velocities in Special Relativity

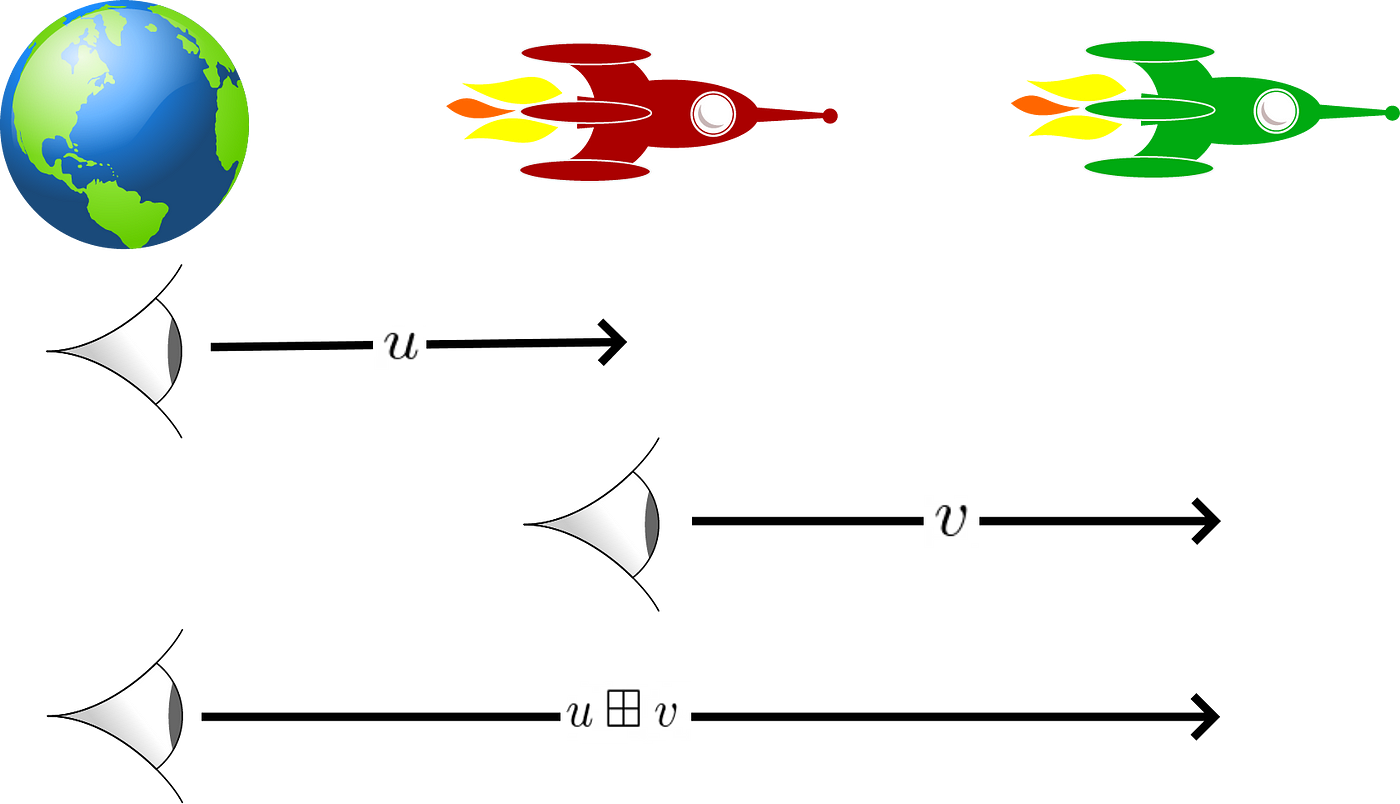
In Diagram 2, u represents the velocity of the red rocket as observed from Earth, v represents the velocity of the green rocket as observed from from the red rocket and u⊞v represents the velocity of the green rocket as observed from Earth. The distance between rockets and Earth is irrelevant. Only velocities are relevant to this discussion.

Velocities add conventionally when small compared to the speed of light but also add in such a way as to not exceed the speed of light when velocities are large. Choosing our units so the speed of light is 1 (for example: seconds and light seconds), we have the following rule for addition:

Similar to probabilities, addition works as normal if u and v are ≪1 but the addition saturates so adding values near 1 produce a result that is even closer to 1 but cannot reach or exceed it. We can follow the same procedure as last time to get a rule for doubling by setting v to u in Equation 9:

And, as before, to get the rule for multiplying by 3, we substitute the value for 2uin Equation 10 for v in Equation 9 and simplify to get:

Quite surprisingly, at least for me, the coefficients for row 3 of Pascal’s triangle have again made an appearance and this continues to the general case:

To multiply a velocity by n:

Go to row n in Pascal’s triangle and place the first 1 under the vinculum (division line).

Place the next coefficient over the vinculum and keep alternating

A Quick Proof

To understand what is going on here, let’s left-justify Pascal’s triangle as shown:

For any given row n, we can now define the Even polynomial (black coefficients) and the Odd polynomial (red coefficients) as follows:

Equation 10 is in the form of Odd / Even polynomials for row 2. In order to finish a proof by induction, let’s take a arbitrary row n and substitute into Equation 9, changing from u to x and then multiply above and below by E:

The key insight here is that multiplying by x shifts all the coefficients right by 1. This means that above and below the vinculum, we effectively have the rule for addition in Pascal’s triangle executed separately for the Odd and Even cases. Here’s how it works for n=5:

It’s quite interesting how all this behavior is contained in the apparently simple Equation 9.

Compare and Contrast

Now that we’ve explored what’s going on, we can concisely summarize the similarities between probability multiplication and velocity multiplication operations:

For values near zero, only terms up to first order are significant and we have O ≈ n.x and E ≈1. When we get to one, all terms are equally significant and E=O, because every power of x will be 1 leaving us with unmodified binomial coefficients. The result of this is that near zero, we approximate to standard multiplication for both operations, whereas when we get to one, by Equation 3, E and O cancel either by subtraction or division.

We can confirm this analysis with a couple of graphs comparing doubling and tripling of velocities and probabilities.

In both cases we are only interested in the interval: [0..1[ (Strictly speaking we could extend to ]-1 .. 1[ for velocities allowing motion in the opposite direction.) As is apparent, the slope near the origin is 2 for doubling and 3 for tripling. Both operations tend to a maximum of 1 as expected with velocity in blue growing a bit faster than probability in red until near saturation.

Conclusion

We could extend from whole number multiplication to reals using the binomial series. We could also explore other candidates for saturated addition such as the first quarter cycle of the Sine function but it’s time to bring this article to a close.

Pascal’s triangle really is a Swiss Army knife of mathematics- it shows up in so many places. If you’d like to find out more, Casandra Monroe discusses some fun properties of Pascal’s triangle on Numberphile. I hardly touched on Special Relativity but Minute Physics has a nice short course also on YouTube.