Mathematical modelling of uncertainty stands or falls on our ability to assess probabilities, but how do you know if your assessments are any good and what does that even mean? This article takes a pragmatic approach to answering these questions. We’ll start in the shadows of the valley of frequentism, step out on to the Bayesian foothills of subjectivism and stride on to the summits of pragmatism and an objective form of the Bayesian view.

From this standpoint, we will see what can go wrong with probabilistic assessments and discuss systematic biases. Finally, the pragmatist interpretation will bring us to a methodology that not only reveals bias, but also makes it clear how well supported the inference of bias is in the data, by showing an uncertainty range that reflects both consistency of bias and the number of data used to reveal it.

To give a sense of the problem, say we assessed at 20% the probability that Stochastic Steel will win the contract they’re negotiating with Bigger Ball Better Ball Ball-Bearings. They win the contract. Was that assessment correct? What does that even mean?

Frequentism

Frequentists believe in objectively correct probabilities, but their only access to these objectively correct probabilities is as frequencies in large (infinite) numbers of repeated identical experiments. They say things like if Stochastic Steel negotiate that contract an infinite number of times then the average number of times they win the contract is the correct probability. But we all know that how ever many times we negotiate the same contract under the same conditions, we either win every time or never at all. If we ever repeat negotiations, it certainly isn’t under identical circumstances. There are workarounds (involving ensembles of possible worlds fixed with respect to the information we have, but variable with respect to everything else), but there’s something very unsatisfactory about an utterly inaccessible notion of probability.

Subjective Bayesianism

Bayesianism is the natural foil to frequentism. Bayesians start with the notion that probability is simply quantified belief and then work out coherent ways to modify beliefs in the light of data. This is Bayes’ theorem, preached in its purest form by the high priest of Bayesianism, E.T. Jaynes. The problem for many Bayesians (though not Jaynes) is that while we know how to update beliefs, it’s not clear where our belief should start before we bring any data to bear. One way out is to give up on objectively correct probabilities and claim it is legitimate to assess that “prior” belief subjectively.

While it’s certainly true that we can elicit subjective degrees of belief, as a normative theory, I find a subjective notion of probability almost as unsettling as an inaccessible one. It’s a terrible licence for all sorts of silliness. Jaynes seeks (and finds) answers in a coherent, objective description of pure ignorance. I will here come at it from the other end and argue that a pragmatic approach to our final assessments of probability brings us, like Jaynes, to a working notion of objective Bayesianism.

Pragmatism

Pragmatism is a philosophical tradition that started in the late 19th century and continues to this day. It is summed up beautifully in this quote from Charles Peirce, one of its founding members

Consider the practical effects of the objects of your conception.
Then your conception of those effects is the whole of your conception of the object

What Peirce is saying here is don’t get too hung up on what objective probability is, think about how you might use it. Think about its practical effects.

The problem with my 20% chance of success is that the outcome is too uncertain: 20%, 4:1 against. Not great great odds, but still more likely than getting out of jail in one throw in monopoly. So even if the 20% is correct, it doesn’t really have any practical effect. To be able to say something a bit more practical, I need to reduce this uncertainty.

Aggregation to reduce uncertainty

If I have a list of probabilities and outcomes — all the contracts Stochastic Steel negotiated in the last quarter, for example — I can look at the total number of wins, which will reduce the uncertainty a bit.

Assuming a notion of correct probability, I can ask myself if my probabilities were all “correct” what would the probability distribution for the total number of wins look like?

If the probabilities are all the same, this is just a binomial distribution, if not then I explain how to do this (and provide an Excel spreadsheet with the methods implemented) in my article on auditing probability sequences. The result looks something like the figure here, where I have assessed twenty contract negotiations.

On the horizontal axis here, we have the number of successful wins and vertically we have the probability of getting that number, calculated directly and with an approximation.

Interpretations

Let’s say we we came in on the low side of our prediction with three wins in the quarter.

A frequentist would say, “the hypothesis that the probabilities are correct is accepted at 90% confidence, but not at 95%”. This is bonkers. No one ever imagined for a second that every single assessment in that list was perfectly accurate, so the null hypothesis whose truth we are trying to establish at some level of confidence starts with a probability that is both practically and theoretically zero. But it’s nonetheless “not refuted” with a particular level of confidence. Happy days. As you were. All is well.

Lucky that there were three and not just two wins, because then we’d have been refuted at 90%. Sad feelings. Refuted. Switch the lights out on the way out

Still, at least frequentists are trying. The subjective Bayesians just quit on objectively correct. They’ve gone fishing.

Can pragmatism do better? Can a pragmatic interpretation of probability help us understand whether that low result was bad judgement or just bad luck?

Bias

Assuming, as we are, that there is such a thing as an objectively “correct” probability, but for whatever reason — congenital optimism, human heuristics, mathematical ineptitude — I consistently and systematically get it wrong.

Interestingly, such systematic biases are the only things we can hope to capture in this kind of analysis. Random errors — going a bit high here, a bit low there, will tend to cancel out in the aggregation we do to reduce the uncertainty. This is the price we pay for aggregation — we reduce uncertainty, but we give up being able to say anything about individual assessments.

A taxonomy of systematic bias

It turns out that because of the ways random variables behave when you add them up, there are only four kinds of systematic bias we can catch.

• Optimism: Consistently pitching probabilities too high
• Pessimism: Consistently pitching probabilities too low
• Polarization: setting probabilities that are a little higher than average much higher than average and probabilities that are a bit lower than average way lower than average— if it’s good it’s very very good, if it’s bad it’s horrid.
• Vagueness: Moving probabilities that are removed from average back towards the average — fence-sitting.

Polarization is a reflection of over-confidence in your ability to assess, or reading too much in to the data. Geologists are terrible at this. Vagueness is rarer, but you do see it, though often as an overcorrection to polarization or because people are gaming their probabilities to get good results on average.

Modelling bias

The pragmatic notion of at least the theoretical existence of a correct probability allows us to build a model for what goes wrong with assessments of probabilities. The basic idea is to use Bayes’ theorem, which as I mentioned tells you how to change probabilities in the light of data or evidence, to alter the true probability on the basis of spurious data. In the case of optimism and pessimism, these spurious data are data supporting or undermining the positive outcome. In the case of polarization and vagueness, they are additional data magnifying the available data that have moved the probability away from its starting point.

It turns out that optimism and pessimism can be captured in a single number, which is positive for optimism and negative for pessimism; and polarization and vagueness can be captured in a single number, which is positive for polarization and negative for vagueness. For the mathematically initiated, bias is modelled simply as a linear transformation of evidence, as I discussed in my article last week. See the endnote below.

The figures above show how true probabilities (red line) are lifted by optimism (left figure, solid lines) and depressed by pessimism (left figure, dashed lines). Polarization (right figure, solid lines) pushes low probabilities lower and high probabilities higher. Vagueness (right figure, dashed lines) brings probabilities back towards an uninformative 50:50.

So now we have a concept of objective, correct probabilities and we have an elegant little two-parameter model for the effects of bias. How do we put these things together to get something useful that also explains what we might mean by objective probability?

The pragmatists “practical effects” of precise probability.

The crucial step is to realize that the concept of objectively correct probabilities allows us to treat our outcomes as samples of the probability distributions described by those correct probabilities. That, in turn, allows us to set up what is essentially a regression problem to work out the bias parameters — those two numbers that describe all the possible forms of bias.

Here’s how it works. We start with our list of biased assessments and outcomes and we wash the biassed assessments backwards through our bias model for some choice of bias parameters to get our objective, putatively correct probabilities. We then compare the outcome predicted by these with the actual outcomes and measure how well that choice of bias parameters fit the data.

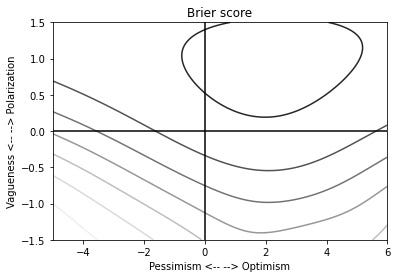
There are two ways of closing the loop. The first just says, OK, choose the bias parameters that give the best fit between prediction and outcome. So here I’ve plotted the mean squared deviation between predictions and outcomes (sometime known as a Brier score). The point where it’s lowest is my regression-fitted bias parameter.

The horizontal axis is the optimism / pessimism parameter and the vertical axis is the vagueness / polarization parameter. So we can see our data our best explained by a modest optimism, flavoured with a squeeze of polarization.

Another, I think, better way of looking at this is to ask, what is the probability of seeing the data we see for a range of choices of bias parameter. This is a likelihood function — it gives the maximum likelihood estimator, which isn’t massively different from the least squares estimate above, but which comes equipped with an uncertainty distribution, which gives a very real sense of how well we have nailed that parameter.

Perspectives

Defining probability in terms of what you do with it and leaping lightly over the ontological bog has proven remarkably fertile. It led us first to the recognition that there are only four systematic biases we can hope to extract from an analysis of probabilistic prediction, and we were able to develop a forward model for these. This in turn allowed us to invert back to the parameters in the model and answer the question we asked ourselves in the first place: are these probabilities any good?

Of course the answer to that is never better than “probably”, at least for any reasonably sized set of outcomes, but at least now we have a coherent sense of the uncertainty that circumscribes that “probably”.

Mathematical endnote

We first transform the true probability to an evidence value, as discussed in my earlier article

Then the bias transform just utilizes that the impact of data (spurious or otherwise) in evidence space is linear. So it’s simply a linear transform

Systematic optimism is a constant addition of spurious supporting data (apositive), pessimism a constant addition of spurious detracting data (a negative). When b is positive, events that are more likely than not are increased in their relative likelihood and the converse is true for b negative. Thus b captures, respectively for positive and negative values, polarization and vagueness.

Finally, we transform back to get back to probability