Pierre de Fermat is Much More Than His Little and Last Theorem

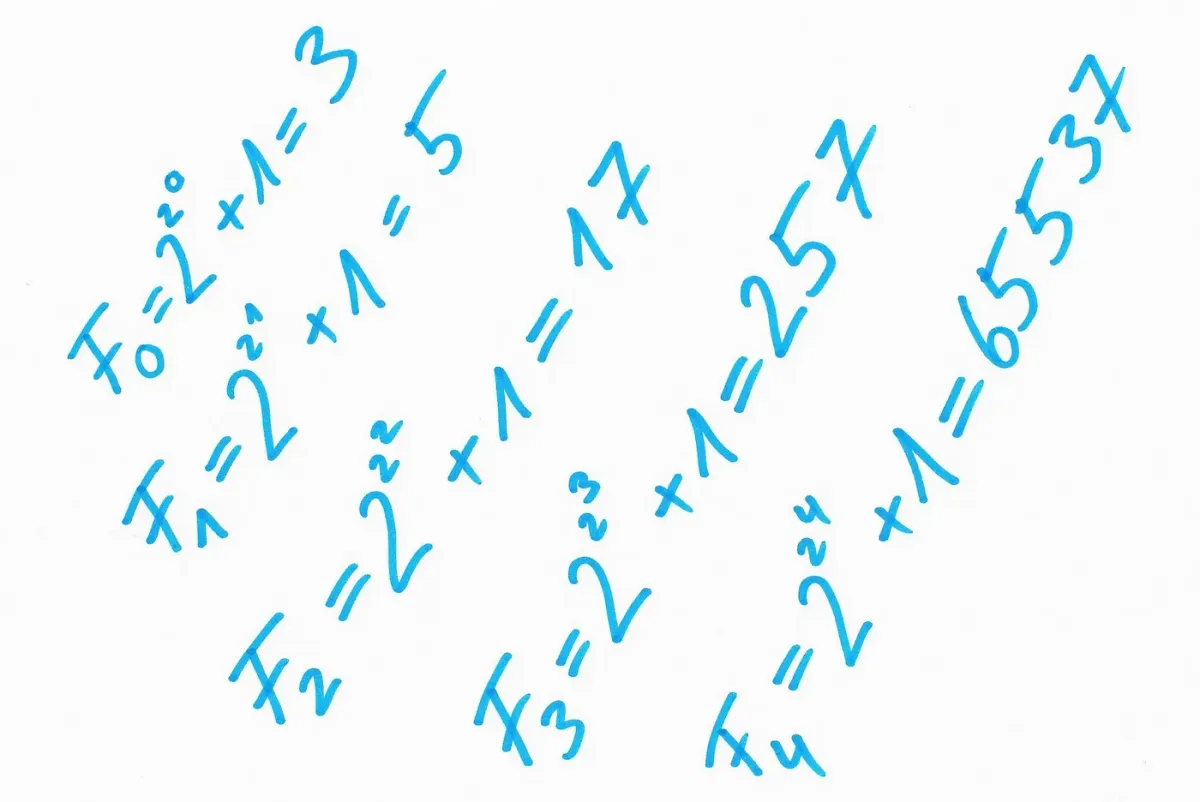
Pierre de Fermat was a genius in many fields. He was a lawyer, mathematician, and fluent in six languages. He contributed significantly to analytic geometry, differential calculus, and his best-known works to number theory in mathematics.

So, during the study in mathematics, you come across him several times.

I still have my notes from the seminar where we went through the proof of Andrew Wiles of Fermat’s Last Theorem. The feelings have been ambivalent at the time. On the one side, there was a great relief in the mathematical community that the theorem was finally proved. And on the other hand, there was the frustrating realization that only very complicated math could prove this theorem and not a simple mathematically beautiful proof.

But Pierre de Fermat is not only the Little Theorem and Last Theorem.

I this article, I give the introduction to Fermat’s pseudoprimes and the Fermat numbers. I also want to show you mathematical thinking and how a result is not the end but the beginning of new questions for a mathematician.

Let’s start with Fermat’s Little Theorem as we will need it further on. Pierre de Fermat made that statement in a letter to Bernard Frénicle de Bessy in the year 1640. It is also the basis of the Fermat primality test.

Fermat’s Little Theorem: If p is prime, then p divides aᵖ⁻¹-1 for every integer a relatively prime to p.

That means that if p is a prime number, then for every integer a, the number aᵖ – a can be divided by p.

17 is a prime number so, a ¹⁷– a is divisible by 17 independent of the integer a. And a can be positive, negative, or zero, it always holds.

The first published proof was done by Leonhard Euler in 1736, although it seems that Gottfried Wilhelm von Leibniz has already proved it in 1680 [1].

Information and proofs of Fermat’s Little Theorem can be found in the comprehensive writing of Jørgen Veisdal.

But this is only half of the story.

For a mathematician, such a result is typically the beginning of the mind journey.

The natural question is always to look at the reversion of such a statement.

If a positive integer n, with n > 1, divides aⁿ – a, with a an integer, is then n a prime number?

Let’s look at the particular case of a = 2.

Fermat’s Little Theorem tells us that 2ᵖ - 2 is divisible by p if p is a prime number.

Now, we want to know if n, a positive integer with n > 1, divides 2 ⁿ - 2, is then nalways a prime number.

This question is more than 2’500 years old and already known by the Chinese.

Indeed, all calculations showed that up to n =340, the only values that divide 2 ⁿ - 2 are prime numbers.

Unfortunately, n = 341 provides a counterexample. 341 is 11 · 31, and thus, no prime number, but it fulfills the statement. So, the reversed statement is, in general, not true.

With the help of the factorization property

We get

And thus, it is divisible by 341.

So, there are integers that have similar properties as primes but are not primes. That leads us to the definition of pseudoprimes.

Definition: Integers that do divide 2ⁿ – 2, but are not prime numbers, are called pseudoprimes.

Having found a counterexample leads us again naturally to the next standard questions about such numbers’ properties.

» Is 341 the only non-prime number that fulfills it?
» Otherwise, how many of such numbers exist?
» Is it an infinite number of such pseudoprimes?

One can show that there is indeed an infinite number of pseudoprimes.

That was shown first for all odd pseudoprimes and after, also for even ones.

Theorem: For every odd pseudoprime, there is a greater odd pseudoprime.

When we can prove this theorem, we have first shown that there exist more than one odd pseudoprime, and second, there are infinitely many odd pseudoprimes. So, let’s see.

Proof: The idea of the evidence is to show that 2 ⁿ - 1 is a pseudoprime if n is a pseudoprime. For n > 1, it follows that 2 ⁿ - 1 is greater than n and odd.

n is a pseudoprime, which means it is a composite of odd integers k and l: n = k · l, with k, l >1. So, with using the factorization (∗) above, we get:

And thus, 2 ⁿ - 1 is a composite.

n is a pseudoprime which means, n divides 2 ⁿ - 2, or equivalent 2 ⁿ - 2 = n · m, for m a natural number.

Now, we have to show that 2 ⁿ - 1 divides

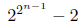
With the same factorization property (∗) as used before, we can show:

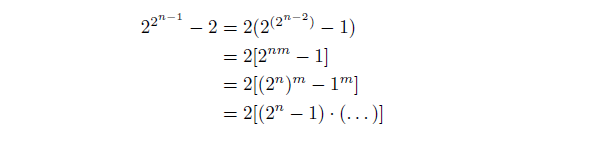
And thus, 2 ⁿ - 1 is a divisor of

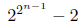
QED

So far, all pseudoprimes are odd.

Does a pseudoprime exist that is even?

For many years this proposition was not clear. But finally, the answer is yes. In 1950, D.H. Lehmer, an American number theorist, found 161038 as an even pseudoprime.

Proof: The prime decomposition of 161038 is 2 · 73 · 1103, and 2¹⁶¹⁰³⁸ – 2 = 2· (2¹⁶¹⁰³⁷– 1).

So, we have to show that 73 as well as 1103 divide 2¹⁶¹⁰³⁷– 1.

By using again the factorization property (∗) stated above, we get the desired results:

161037 = 3²· 29 · 617 = 9· 29 · 617

Thus,

And similar:

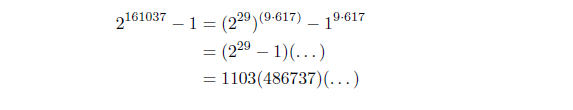
73 and 1103 are primes, and thus, the divisibility of them does not affect the other, and both divide 2¹⁶¹⁰³⁷ –1, and therefore, 2 · (2¹⁶¹⁰³⁷ – 1) is an even pseudoprime. QED

In 1951, the Dutch mathematician N.G.W.H. Beeger also proved that the number of even pseudoprimes is also infinity. The proof uses similar arguments as for the case of odd pseudoprimes and the fact that for every even pseudoprime n₁, there is a prime p such that n₂= n₁ · p is also an even pseudoprime.

I omit the details of this proof.

That leads us to the absolute pseudoprime, also called absolute Fermat pseudoprime, or Carmichael number, named after Robert D. Carmichael, an American mathematician.

Definition: A composite number n that divides 2ⁿ – 2, and 3ⁿ – 3, and 4ⁿ – 4, …, and aⁿ – a, and … for every integer a, is called an absolute Fermat pseudoprime, or Carmichael number.

The obvious question is whether or not such a number exists.

And indeed: 561 is such a number, as well as 1105, 1729, 2465, and so on.

Let’s prove first that 561 is a Carmichael number.

Proof: We have to show that 561 is a composite and divides a⁵⁶¹ – a, for all integer a.

561 can be decomposed into the primes 3 ∙ 11 ∙ 17.

Thus, we have to show that a⁵⁶¹ – a can be divided by each of these primes. Applying again the factorization property (∗) from above, we get

and from Fermat’s Little Theorem, it follows that it is divisible by 11. Repeating this procedure for 3 and 17 completes the proof. QED

When we look at the decomposition of other absolute Fermat pseudoprimes we get the following picture:

The next logical questions arising are:

» Are there any absolute Fermat pseudoprimes with less than three prime decompositions?
» Are there any even Carmichael numbers?

To explore that further, we need the following definition:

Definition: An integer is called squarefree if it is not divisible by a perfect square other than 1.

With this, we can introduce Korselt’s criterion:

Theorem: A composite integer, n>2 is a Carmichael number if and only if n is squarefree and for every prime p dividing n, also (p - 1) is dividing (n - 1). [2]

The above questions are answered by the following theorem that states:

Theorem: Every Carmichael number n is odd, has at least three different prime factors, and every prime factor of n is less than √n.

Proof (only a sketch): To show that n is odd, we use the concept of coprime. That means that the only positive integer that divides n-1 and n is 1. In other words, their greatest common divisor is 1.

Because of the definition of a Carmichael number, n-1 and n must be coprime. Using the definition, the factorization property (∗), and the fact that

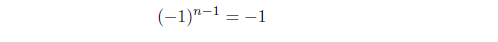
for n-1 even shows this that n must be odd.

For the second property, we set n = p ·q for p and q primes, i.e., n consists of only two primes. Because n is squarefree, we also have p ≠ q. So, without any loss of generality, we can assume that p > q. With the use of Korselt’s criterion, we would get the conclusion that (p-1) divides (q-1), which is a contradiction because p > qand thus, p-1 > q-1. So, n cannot consist of only two prime factors and needs to have at least three.

Also, the last part is again proven by some factorization work. If p is a prime factor of then, we can show that p ≤ n / p. It would be equal if n² = p, which contradicts the squarefree property, and thus, the inequality must be strict. QED

Even though only 2’163 Carmichael numbers are smaller than 25 billion, in 1992 (published 1994 [3]), it was proven that their number is infinite.

The proof shows that C(x) > xᵞ, where C(x) is the number of Carmichael numbers up to x, and γ = 2/7. The derivation of the proof needs several advanced arguments from number theory.

That means letting x approach infinity, xᵞ , with γ = 2/7, approaches infinity, and thus, the number C(x) of Carmichael numbers approaches infinity, too because C(x) > xᵞ.

This all leads us finally to the so-called Fermat numbers.

Definition: The numbers

for n = 0, 1, 2, … are called Fermat numbers.

The first few Fermat numbers are:

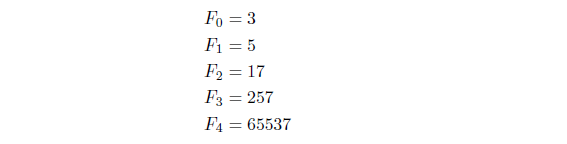
These numbers have been known at Fermat’s time, and all are primes. So, Fermat claimed that all Fermat numbers are primes without giving proof.

The next Fermat number is

Euler proved in 1732 that F₅ is divisible by the prime 641, so this Fermat number cannot be a prime.

And not only that. So far, F₀ to F₄ are the only known Fermat numbers that are prime.

But how to prove that, and where do we stand today?

One has actually to prove that the Fermat number is divisible by a prime. Today, this is done by algorithms and intense computational power.

The latest Fermat number where it could be shown that it is not prime is F₁₈₂₃₃₉₅₄. It is so far the biggest Fermat number known.

But not for all Fermat numbers up this one could it be proved that they are not prime. The full list of Fermat numbers where at least one prime factor is known and thus, proven that it is not prime can be found on the Fermat Numbers Divisor project page.

When you are interested in that topic, you can support finding new factors by joining the project. There are still many ranges of Fermat numbers available to solve.

That also shows a recent development in mathematics. Many applications cannot be anymore calculated and proved in a closed form, i.e., by using a finite number of functions and standard operations. Only solutions by computationally intense calculations bring us forward. And it shows how a simple problem can become quite complex to solve. That’s one of the beauties of math.

References:

[1] D. Mahnke, Leibniz auf der Suche nach einer allgemeinen Primzahlgleichung, Bibliotheca mathematica. Zeitschrift für Geschichte der Mathematischen Wissenschaften, 13, 1912, 29–61

[2] A. R. Korselt, Problème chinois, L’intermédiaire des mathématiciens 6 (1899), 142–143

[3] W.R. Alford, A. Granville, and C. Pomerance, There are infinitely many Carmichael numbers, Annals of Mathematics, 140 (1994), 703–722