I love patterns and take great joy in searching for them. During my 11th grade, we came across the question:

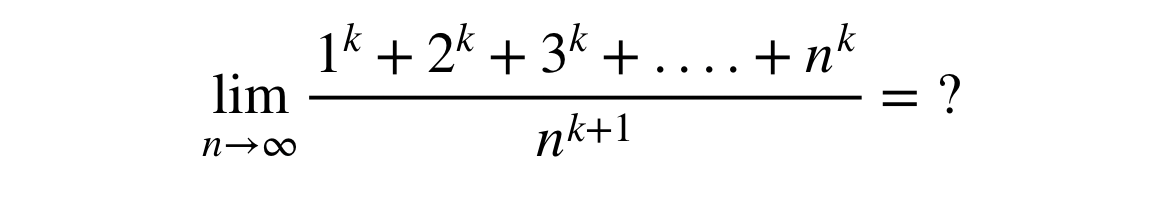
Our professor suggested that there is no general formula for the summation in the numerator and we ended up solving the problem using integration.

However, this left me on a search for a general formula for the sum of powers of the first n natural numbers.

This section describes my research approach to the above question

I approached the question by finding the formula for known values of k and thereby try and generalise the results for any value of k

Let us express the sum as

For k = 0,

For k = 1,

For k = 2,

For k = 3,

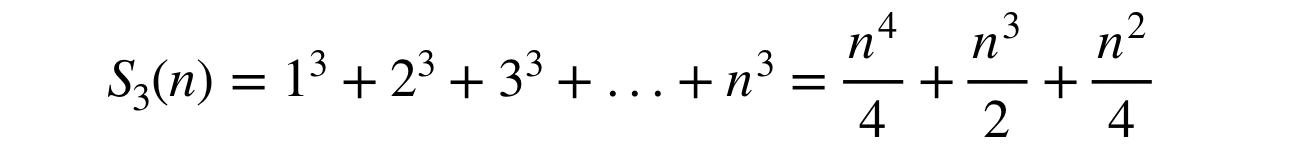
For k = 4,

By this step, I felt a pattern emerging for consecutive values of S. It goes like this:

I use the approximate symbol here to point out a specific modification to the integral.

Post-integration, in case we run out of n¹ and n² in the equation, we just add them along multiplied by a constant. For example:

In such cases, we add factors for n¹ and n²

As we can calculate the values of the sum for various n, we find out the values of k_1 and k_2. Here, we get k_1= 1/30 and k_2 = 0. Therefore, we have

Using this trick, I could calculate the formulae as far as k = 21. Some of them are:

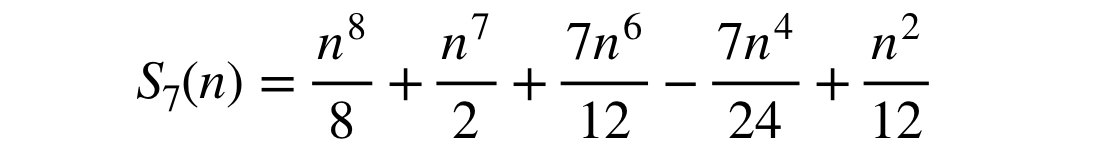
Note: I checked S9 from Bernoulli’s Ars Conjectandi and found it to have an error in the n² term.

Now, what caught my eye were the numbers popping up as a factor of n every time we “modify” and complete our integral. It was like magic. What were these numbers?

One peculiar feature was that these numbers originated only for even power summations, such as k = 2, 4, 6, 8, etc.

The “magical” numbers for some values of k:

I made a note of these numbers and paused my research at this point. As time passed by, I entered university and started reading on various topics in mathematics. During one such session, you should have seen the excitement on my face when I stumbled upon these exact numbers at the Reimann Zeta Function.

Zeta Function

Our summation was concerned about adding powers of natural numbers. The Zeta function is about adding the powers of reciprocals of natural numbers.

Bernoulli numbers are represented by B followed by a subscript 2n as Bernoulli numbers on 2n+1 places have a value of zero.

The Zeta function in its expanded form contains Bernoulli numbers, similar to the summation in the previous section.

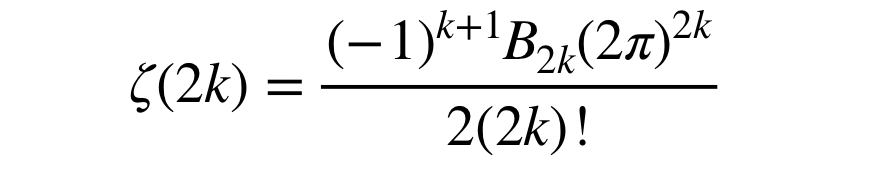
We finally have

Bernoulli numbers appear in various series expansions, a crucial one among them being

At one point I was obsessed with nothing but this question alone. It was the only thing on my mind. And now I had a solution right before me, given by one of mathematics’ greatest more than 300 years ago. I had mixed feelings at that time — on one hand, it was this great feeling of rediscovering some of the most crucial numbers in all of mathematics. On the other, accepting the fact that my research was not new after all. Probably, this was what a part of life is about. Learning, discovering, rediscovering, and overall accepting the truth.

This is my story on how a single question led me on a path to rediscover some breathtaking numbers teaching me a valuable lesson about life along the way.