If you were to go for a little gambling about what it is going to be about then, most likely, you would hit the jackpot. So why not to try? A croupier has opened bets, waiting for your one, spinning a wheel after a while. Over time, when the wheel’s speed decreased to a decent value, the winner becomes clear. It comes to a halt, and the croupier says, “Gravitation just win!”

Yeah, I am sure it was your dark horse.

Newton partially answered the question, which laid on humans since ancient Greece. That is, how and why do objects fall. He based his concept on earlier works of Tycho de Brahe and Johannes Keppler. These led him to take care of the how part, leaving the why for the next generations to decide, which, as you know, Einstein figured out.

The problem Newton struggled with was how to treat the mass of a planet outside it. He intuitively felt that thinking of it as a point-mass is correct. Yet, hunch does not mean to know. Proofs are what make theories obtaining scientific value. And he did it after 20-years. I can only imagine how much joy jumped out from him when he gets there. It had to be for him like taking a breath after a deep dive.

In school, we learn that gravity is the product of two masses times the gravitational constant divided by the squared distance. Putting it into an equation:

When it comes to planets, we take the distance as the separation between its center and a given point in space without even thinking about what miracle of miracles it is. How all forces, dF, exerted by mass points, dm, contributes to the net-force like the planet’s mass would concentrate at its center. But there is one restriction: uniformly distributed density on an entire sphere.

Yet, it is not any problem. A planet might be thought of as infinitely narrow shells, from the outermost to the innermost. Where the center for each is at the planet’s center and within which roughly the same density prevails.

So, let us go and prove that the gravitational force of a planet behaves as all its mass would be at its center.

The proof

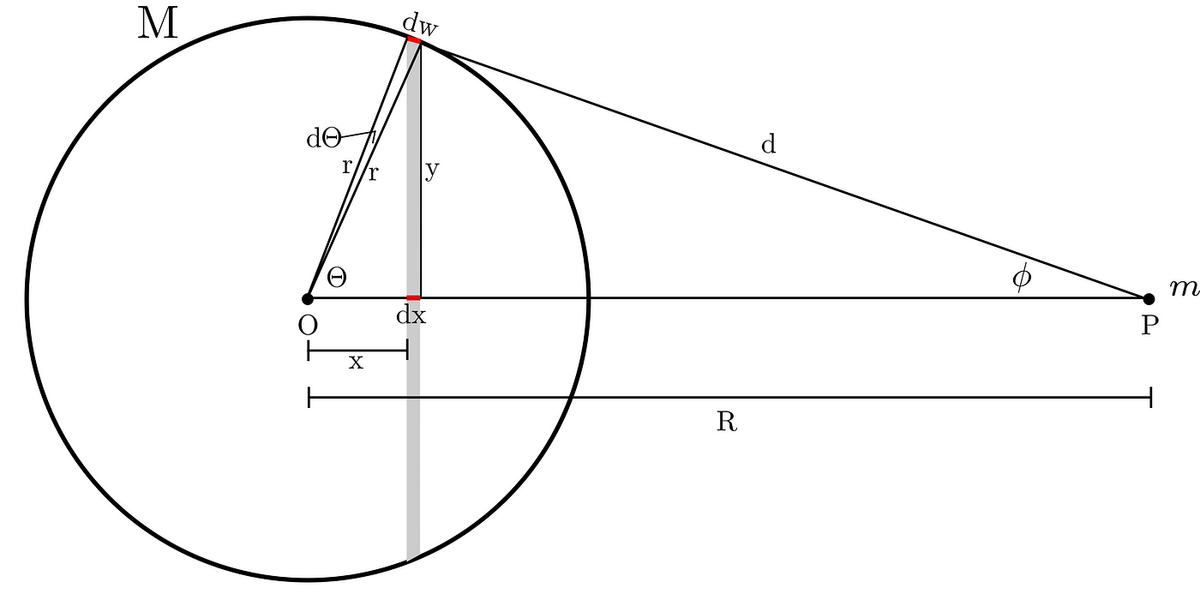
In the beginning, setting a stage is always a good idea, so below is ours.

The circle represents a single shell of a planet. It has a radius r, density σ, and mass M.

Next, each shell might be divided into an infinite amount of rings. Where each has an infinitely small width, dw, fixed distance, d, to P, and mass, dM. Also, each shell has its center at point O, which is distance R from point P.

Now, we should add all forces, dF, exerted by rings on P. Starting from the one above. Yet, notice that from symmetry, only component along R will count. Why? Namely, the vertical component (y) of each force exerted by any point- mass contained in a ring has its counterpart. So, the net-force of the ring:

Where dM, as we said, is mass of the ring, which is its area times density. The area of a ring is given by its circumference, 2πy, times its width, dw. So, putting it all together we get:

But, notice that r ⋅ sinΘ is equivalent to y and r ⋅ dΘ to dw. Thus:

Finally, by writing down the density of the shell as M/4πr²:

This dM might be now substituted into the force equation.

It has 3 independent variables: d, θ, ϕ. They have to be reduced to a single one. What we can do is take a look at the law of cosine and use it in our favor. Hence:

and

However, instead of cosθ, we need sinθ ⋅ dθ. That is why we should differentiate both sides of that equation to get what we want.

And d has become our only independent variable. Just look, how the gravitational force equation looks now.

That is the force exerted from a single ring.

The last step is to sum forces from all rings of the shell. Yet, summation means integration. In our case, from the rightmost ring to the leftmost. It matches to integration limits from d=R-r to d=R+r.

Evaluating this integral gives the answer we were looking for.

Indeed, as we assumed, all gravitational forces from tiny-little points on the entire shell contribute to the net-force like all their masses were located at its center.

Each time, when results like this pop out from calculations, I realize more and more how much symmetrical our world is. Maybe it is even an appreciation. Yeah, I think it is.