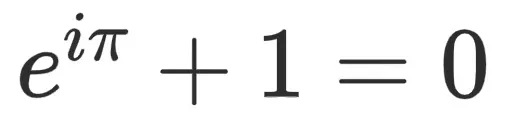
In mathematics, it is often the case that we derive things through proof or previous results that we don’t fully understand. Allow me to explain in four simple, interesting examples.

Part One: Euler’s Identity

This is popularly known as Euler’s identity. If you ask anyone remotely familiar with the study of mathematics, they’ll recognize it or admit their familiarity to it. The most interesting thing about mathematics — to me — is the idea of discovering things that we don’t exactly understand.

This is one of those things. The transcendental numbers, which we find popping up in places and we regularly use. Either for half-life, or figuring out the interest rate on your home, or computing the ratio of a circle’s circumference to its diameter.

We know about the necessity of the number 1, which, when subtracting from itself, yields 0. With 0 and 1, and the definition of the square root of negative one, sprinkling in the regular axioms we have for uniqueness, we can construct our entire system of numbers.

We have all this knowledge in this one equation. But we don’t know why.

It’s kind of like gravity, in that Newton knew there was a force acting on an apple falling from the tree. But, to this day, we still have contention about what it exactly is.

Professor Keith Devlin (1947-) of Stanford University said about Euler’s identity:

“Like a Shakespearean sonnet that captures the very essence of love, or a painting that brings out the beauty of the human form that is far more than just skin deep, Euler’s equation reaches down into the very depths of existence.”

Benjamin Peirce, philosopher, mathematician, and Harvard professor, has also said that it “is absolutely paradoxical; we cannot understand it, and we don’t know what it means, but we have proved it, and therefore we know it must be the truth.”

And that is really the heart of what Euler’s identity is. In fact, it is the heart of a lot of mathematics. A push for heavy rigor in proof work and completion and organization of infallible logic. But even with the entire arsenal of logical thought and precision thrown at it, it falls short of actual true meaning. Much like gravity, Euler’s identity exists. That is without a doubt a truth.

We use the elements involved in the identity. We have them show up in many of the applications invented to date. We find them in disciplines far removed from pure mathematics. We know they explain reality as we know it to a highly precise degree. They model nearly everything we come across. They’ve bettered the lives of the vast majority of society without society acknowledging or recognizing it. They are invisible truths of the world. You don’t need to know them to benefit from what they have given us.

But, if someone were to ask me, “why?” is Euler’s Identity, I couldn’t tell you. That’s the funny thing about it. You have an equation so powerful, connecting so many brilliant elements in mathematics — and so gracefully — but we don’t truly understand it.

Part Two: Compound Interest

Remember how we saw e in Euler’s Identity up there? It’s connected to a lot of things, but let’s start at its discovery and then move into its weirdness.

In 1683, Jacob Bernoulli asked a question about compound interest:

An account starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2.00. What happens if the interest is computed and credited more frequently during the year?

Meaning, if you take the initial dollar, and divide the interest (100%) into the number of times you want it to pay out, what happens? If you wanted it done twice, you would have 50% each 6 months. Meaning, you’d have, in dollars,

This just follows the format that you’ll multiply your dollar by

Where n will be the number of times you want your initial 1 dollar compounded. In other words, you’ll be dividing the 100% interest into as many pieces over time as you’d like. For example, in our original case for each 6 months, you’d have, in dollars,

The interesting thing for Bernoulli quickly became how to answer this for large values of n.

For n = 12, you get $2.613035.

For n = 52, you get $2.692597.

For n = 365, you get $2.714567.

And then, for n infinite, you get

2.71828182845904523536028747135266249775724709369995…

Infinity has a weird relationship with mathematics. On the one hand, it has rendered humankind the ability to look deeper into the inner workings of the world.

On the other hand, it begs the question, “why?”

Another transcendental number pops up similarly through the use of infinity:

Where C is the circumference and d is the diameter.

But how did we come up with this? Why is the shape a circle? What exactly is a circle?

You are starting from a square, continually adding sides.

To infinity.

And, at infinity?

3.14159…

So, when you look at a circle, you’re actually looking at an object that has an infinite number of sides. This idea of the derivation “yielding” us the result goes further.

If we revisit the curiosity for Euler’s number, we’ll see even more head-scratchers. Namely,

We take what motivated Bernoulli’s compounding example and expand to exponentiation. That is, we look at e as a transcendental constant that is the base of our exponential function. And again, even as a function, it has a curious power in its mysterious existence.

The definition of the exponential function is something almost everybody has come across. You learn in grade school at some point that

We learn later, that if you want to take its derivative, you get

One thing to take from exponential functions is how quickly they grow. Speed and acceleration are at the heart of exponentiation.

So when we are taking the derivative of

We are motivated to find the constant b such that ln(b) = 1. We are motivated to find the constant such that the rate of increase is the original function. Which means, by verifiable recursion, that the rate of the rate of the increase will also be the original function. Which means that any nth iteration of the derivative of the original function or the nth iteration of the nth derivative will also be the original function. Again, we revisit the notion of infinity.

The constant, e, is the unique base for which the constant of proportionality is 1, rendering the derivative of the exponential function with base e equal to itself.

The treatment of the transcendental constant, e, is a strange one. Unlike the other exponential functions, it has a lot of derivations in all sorts of fields with equally perplexing interpretations and meanings. For a better look:

Where

is our limit involving our initial question with Bernoulli and compounding (For the special case where x = 1, and it yields e).

There is no question that these special irrational numbers, e and π, have given profound insight into the nature of the world and the behavior of the materials and objects in them. Whether it is in distributions, sound-waves, atoms and subatomic behavior, gambling, biology, chemistry, physics. We have a seemingly endless list of contributions it has made. All from a human who initially wanted to answer a simple compounding question.

But in the quest for some closure, and some convergence, it seems like we still diverge. For every issue tackled, many more arise. In the same vein that the transcendentals arise. Arise, but don’t necessarily lend meaning into “why”. These numbers, e and π, are discovered through curiosity and the power of human will. I’d say today we stand knowing as much about either of these numbers as we’ve ever had. In fact, we calculate each of these to trillions of decimal places.

The history of finding more as perplexing in our attempt to understand its existence.

Part Three: Taylor Series

For e above, the Taylor series is

Which for e to the exponent one yields

We know that this series converges. We know that this series converges to our transcendental constant, e. Another series we know that resembles this one is the harmonic series:

Interestingly, you’d want to say that this thing will converge. The sum of the first million terms is approximately 14.8. But if we assume the harmonic series converges, then we can assume that

Then

But

Hence

which is not possible. As such, we know the series to diverge.

However, in 1914, A.J. Kempner published a paper titled “A Curious Convergent Series”, which proved that the harmonic series

with a slight modification, actually converges. Namely, it is the harmonic series with the values in the denominator containing “9” deleted. I’ll include a link to the proof below along with other literature on Kempner’s series. Originally, Kempner thought the upper bound of the series would be below 80. Since then, further refining has shown the series to converge to a value slightly below 23, approximately 22.92067. Which is extremely bizarre when you first think about it.

Deleting elements out of a series that diverges will eventually allow the series to converge. But most of the three digit denominator values contain “9”, and it allows the series to collapse barely fast enough. But it obviously begs the question: What are the smallest amount of elements that you can delete out of the harmonic series to allow it to converge?

Part Four: The Ramanujan Summation

If you went to your calculator, and started adding 1 + 2 + 3 + 4 + 5 all the way up and never stopped, you would think you’d get some really huge positive number.

You would be absolutely wrong.

Let me tell you something that completely defies intuition:

Meaning that, if you added the natural numbers, 1 + 2 + 3 + 4 + 5 + … you would get

First, we need a few tools.

So let’s start with the third sum, N₂. If we stop this sum at an even point, we know from symmetry that the sum would be 0. If we stop it at an odd point, it would end up being 1. Without getting into the weird mathematics of it, we take the average. We say that the sum is 1/2. You can check out Grandi’s series here.

Now let’s take a look at our N₁, or second sum. Specifically, let’s multiply the sum by 2.

As you can see, if we vertically add this duplicated sum, we essentially get:

Which we know already to be N₂, which is 1/2. So 2(N₁) = 1/2 so N₁ = 1/4. So now we basically have everything we need to make this mathematical magic happen!

Let’s take our main series, N, and subtract it from N₁:

And what do you know, we have our original sum, N, in our parenthesis! Now we have N−N₁ = 4(N). And we know that N₁ = 1/4. So all we have to do is subtract N from one side, and now we have:

-1/4 = 3N.

The sum of all these positive numbers.

My only addendum to this result would be that the infinite series actually diverges. Also, my end result relies on partial sums of other — infinite — series.

If you are wondering about the usefulness of the result, you can learn more here.But, for the fourth time, if you were to ask me “why?”, I still couldn’t tell you!