Sequences and convergence

A sequence of real numbers is simply a list of real numbers, where for any integer n, you are allowed to receive the nth number in the list. Fortunately, mathematicians deal in theoretical objects, so we never run out of memory, and never get stack overflows from recursive definitions.

A famous example of a sequence of real numbers is:

0.9, 0.99, 0.999, 0.9999, 0.99999, …

where the Nth number in the list has N nines following the zero.

We say this sequence ‘converges’ to 1. Why? The short and cheeky answer is to read the answer I wrote here. But I’ll explain again. The first term is only 0.1 away from 1, the second term is only 0.01 away from 1, and the Nth term is 0.00…01 away from one, where there are N zeros preceding the 1, i.e. 10^-N away from 1.

So a good definition for convergence to 1 is: for any maximum distance from the target you specify, I can find an N such that all terms after the Nth sequence are within that distance from 1.

This definition makes sense. If you set the target to be 0.00234, then we observe that 0.001 is smaller than 0.00234, and that from the third term onwards:

• 1–0.999=0.001≤0.00234
• 1–0.9999=0.0001≤0.00234
• 1–0.99999=0.00001≤0.00234
• and so on

Clearly, whatever you set the maximum distance we are allowed from one, eventually we can find a 0.000000000000000000…00000001 which is smaller than that number, and use the same argument as above.

Subsequences

Subsequences are where we pick out some terms in the sequence, but don’t have to include them all. You can imagine moving along the sequence of numbers and occasionally picking one out to be in your new sequence.

For example, we might have the sequence (0.9, 2, 0.99, 2, 0.999, 2, 0.9999, 2, …)

If we wanted to find a convergent subsequence in the above sequence, all we need to do is ‘ignore’ the 2’s and we get a sequence (0.9, 0.99, 0.999, 0.9999, …) which we have already shown converges to 1.

Bounded

A sequence is bounded if there are two numbers, a, and b, such that every term in the sequence is less than b and greater than a.

If we look at the sequence (0.9, 2, 0.99, 2, 0.999, 2, 0.9999, 2, 0.99999, 2…) again, then we see every term in the sequence is less than 100 and greater than -100.

You might have noticed that the above bounds could be a lot better. But, in this case, it doesn’t matter. In a lot of Analysis, key distinctions are often not in the numerical size of bounds, but whether they exist at all!

A short note on structural properties

Often when we deal with properties like boundedness, we look at what I would regard as ‘structural’ properties of a mathematical object, which tell us a lot of information about how we can manipulate the object without necessarily knowing much else about it.

For instance the interval of all numbers between 0 and 1 is different from the interval of all numbers between 0 and 1,000,000. However, it turns out these two mathematical objects have basically the same structural properties.

In mathematics we often end up manipulating objects which we have proven to exist, without actually knowing what they are! However, if we know useful structural properties we can create mathematical objects which we can manipulate nicely, even without knowing much else about them.

What is a Real Number (Optional)

What is a real number?

It’s perhaps not the most rigorous approach to define a real number after talking about them in sequences and convergence. However, it turns out we define real numbers through sequences, so I wanted you to be comfortable with them first.

The first weird thing about real numbers is that we can’t actually use them on computers. Think about the number pi. It’s got an ‘infinite number of digits’, so we can never actually write it all down, only generate as many digits as we want or have time to create.

We can treat a real number as a sequence of rational numbers, where the distance between numbers in the sequence tends to 0. We say two sequences are the ‘same’ real number if the distance between elements in the two sequences tends to 0.

This formalisation is helpful in some contexts and not helpful in others. Most of the time we use real numbers we don’t really care the build specifications, just as when you buy a car you rarely look under the bonnet. However, an understanding of how the reals are built can be very illuminating for deep applications. E.g., see Cantor’s Theorem. Also, similar ideas are used in advanced analysis to build complicated objects from simple ones. In Measure Theory, ‘measurable functions’ are built from very simple functions

Using our knowledge: The Bolzano-Weierstrass Theorem

The Bolzano-Weierstrass Theorem states that any sequence of real numbers which is bounded has a sub sequence which converges. It is the first of several ‘miracle’ results, which allow you to really see why calculus works.

We use an unconventional approach, namely we prove it using bisection search, as this will be more familiar to the coders among you!

Proof

Let us assume that we have a sequence, where every element is no smaller than 0 and no greater than 1. (to extend this to an arbitrary lower bound a and upper bound b is conceptually the same idea, but looks less elegant).

As every number in the sequence is a real number, it has a binary representation. For instance, 0.5 = 0.1, and 0.6 = 0.100110011001001… Note that some numbers won’t have a finite number of terms — and that’s okay. It’s a floating point representation with ‘infinite’ accuracy!

Why are binary representations nice? Because they allow us to ‘bisect’ the real number line very easily, and do so recursively. If we look at the first 2 binary digits, this creates a natural way to split the real numbers in [0,1] into 4 sections: those whose first two binary digits are 00, those whose first two binary digits are 01, 10 and 11. This corresponds to splitting [0,1] into the intervals [0,1/4], [1/4, 1/2], [1/2, 3/4], [3/4,1]. We can to likewise with 3 binary digits, in which case we will split [0,1] into 8 regions of width 1/8.

The image below captures the essence of what we are going to do.

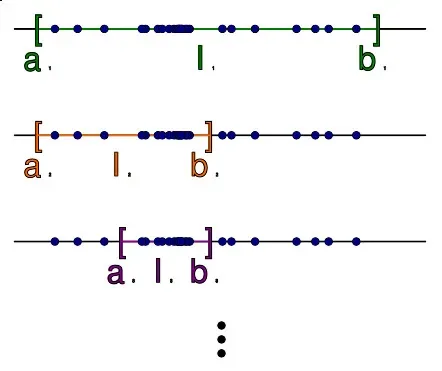
We pick the first element of our sequence. This is at most distance 1 away from any other element in our sequence, as all elements are between 0 and 1.

Now, we divide the real number line into two halves. Those greater than 1/2, and those less than (or equal to) 1/2. Or, those whose first binary digit is 0, and those whose first binary digit is 1.

As these are only two halves, and we have an infinite number of terms, at least one of these two catchment areas must include an infinite number of elements of our sequence. For instance, if the first half only had, say, 17 elements, and the second half had 31 elements, then that would mean only 48 elements in total, whereas there is actually an infinite number.

So, we pick the catchment area with an infinite number of elements of our sequence, and we pick our next term from it. Let’s call this Catchment Area 1. Of the infinite number of elements in Catchment Area 1, this element is at most 0.5 away from all elements in this catchment area, as Catchment Area 1 has width 0.5. Visually, this is because Catchment Area 1 is a line of length 0.5

We illustrate this below. The real interval is split into two buckets. An infinite number of terms of the sequence (blue balls) fall in one bucket, and only four in the other. The first bucket, which we label Catchment Area 1, consists of all terms in the sequence whose first digit in their binary expansion is a zero. (If the first binary digit is a zero, then the number is less than or equal to 1/2).

Now, we take this area, cut in half again.

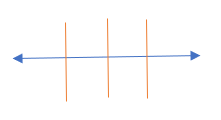
As there are an infinite number of elements in Catchment Area 1, if we cut it in half, there are an infinite number in at least one of the two halves! Visually, below we split Catchment Area 1 into two buckets. In this case, the right hand bucket in it has an infinite number of terms. All elements in this bucket have first digit 0 and second digit 1. As they have first digit 0, they are in Catchment Area 1, but as they all have the same first two digits, the maximum distance between any two of them is now only 1/4.

This can be thought of as defining their second binary digit. In the above example Catchment area 2 is all numbers whose first binary digit is 0 and their second binary digit is 1.

So, we choose the half with an infinite number of elements and call it Catchment Area 2, (if they both have an infinite number of elements in, we pick the smaller half, but it doesn’t really matter). We pick our third element from Catchment Area 2. Catchment Area 2 has width 1/4, so all elements in it are at most 1/4 away from each other.

Notice that, when we pick the second term in our subsequence from Catchment Area 2, this term is in Catchment Area 1 as well.

In general, the Nth element we pick will be in Catchment Area N, which will have width of 0.5^n, and will be in all previous catchment areas.

Here’s some pseudocode. Well, it’s a frankenstein maths-code hybrid. Sorry.

sub_seq = []
Catchment_Area = [0,1]while True:Split Catchment_Area into 2 halves
Pick the half with an infinite number of elements in
Update Catchment_Area to be this half
Pick an element from Catchment_Area, and append it to sub_seq

Now, we have convergence. Why? Because we use binary to specify every digit! The first half we picked, Catchment Area 1, was either all real numbers with first binary digit 0, or first binary digit 1. We pick the first digit of our number to be 0 or 1 accordingly. Catchment Area 2, then specified our 2nd binary digit: it split a space of width 0.5 in half by looking at the the 2nd binary digit. In Catchment Area 3, we split the space again by looking at the third binary digit. In the visual example, Catchment Area 1 specified that the first binary digit was a 1

Thus, we can define a number by choosing its decimal expansion to put it in every single catchment area! We have convergence, because the Nth term (and beyond) of our subsequence is in the Nth Catchment Area. So from our Nth term onwards, all terms are at most 2^-N from the number we constructed, as the number was constructed to be in the Nth catchment area.

For instance, (in binary), you might set the distance target to be 0.01=1/4. No problem. The second term onwards of our sequence is in the second catchment area, and everything in the second catchment area is within 0.01 of each other because their second (binary) digits agree.

And, … we are done!