Logic, Intuition and Paradox

Every once in a while, we will see some breaking news about Artificial Intelligence (AI), the discipline of automating how we think. Not very long ago, there was news stating “[there is] no need [for humans] to prove mathematical theorems anymore!”, referring to a 2019 Google paper (Bansal et al., 2019) about using AI to prove mathematical theorems. This news implies that AI will eventually replace mathematicians.

The idea of AI replacing mathematicians was attributed to the study of logic, which can be traced twenty five centuries back to Aristotle, who identified intuition and logic as being the two aspects of the mind that attain knowledge. However, before the computer, logic became preferred over intuition for its rigor and certainty, which allows logical reasoning to be formally studied and ultimately automated. The computer was the result of a more than two-millenium movement to push the limit of logical reasoning, which culminated in automated logical reasoning without the human mind. However, it turned out that logical reasoning, as well as its automation, is insufficient, and therefore that intuition is indispensable for mathematics. Paradoxically, after we learned about the limit of logical reasoning, we made a new tool, the computer, to leverage our intuition. History has come full circle from Aristotelians seeking to make mathematics so meaningless that it could be done by machines to Platonists wondering if machines could truly understand the meaning of mathematics as we do.

Among many AI research areas, AI replacing mathematicians, which is effectively AI before the computer, has a special and supreme place because its efforts and failure led to the invention of the computer. Revisiting how modern AI can replace mathematicians might help us find the last missing puzzle piece, or how mathematicians think, which could be applied to every form of knowledge development, including AI itself. Amidst the fears of malicious AI mirroring our dark side, it might be delightful to see if AI could imitate the finest among us: the great mathematicians, scientists and thinkers.

The mind studying itself is a self-reference, which often leads to paradoxes. In this article, I frequently use “paradoxical” not because I run out of words to describe how surprising and unpredictable the story is, but because every part of it is literally related to a paradox, which is a recurring theme and an agent of scientific advancement.

How to Kill an Android?

In one episode of StarTrek, Captain Kirk encounters a group of rogue androids who bring down the entire starship Enterprise crew, and plan to destroy all of humanity because they logically believe humans cause all the problems in the universe. To defeat such a powerful enemy, Kirk plans to use “wild and irrational logic” as a potent weapon. Finally, the leader of the androids, Norman, was destroyed by the wildest and most irrational logic of them all, the liar’s paradox.

Kirk says whatever the conman, Mudd, says is a lie, and Mudd says to Norman, “Now listen to this carefully, Norman. I am … lying.” Struggling to resolve the paradox, Norman smokes and crashes; thus we see the death of an android. The liar’s paradox can be illustrated in the following picture:

The paradox comes from “this sentence” referring to the whole sentence of which ”this sentence” is a part. If we assume what the sentence says is true, then the sentence is false, since this is what it says. This contradicts our assumption. On the other hand, if what the statement says is false, then the opposite of what it says must be true, meaning this statement is true, yet another contradiction.

A paradox is the worst enemy of logic. See how it causes the demise of Norman, who is portrayed as following logic strictly. In fact, Norman’s logical brain would have run into a type of self-referential paradox, similar to the liar’s paradox, if he had contemplated questions about himself. Norman metaphorically reflects how mathematicians confront self-references and their consequent paradoxes.

Aristotle: The Power of Logic

Aristotle, a Greek philosopher and polymath (384–322 BC), was the father of logic who studied how we reason rationally in a formal way, instead of investigating it case by case. He considered logical reasoning independently from the contexts where it might be applied. For example, “All men are mortal. Socrates is a man. Therefore, Socrates is mortal,” is an application of the syllogism “All A are B. All C are A. Therefore all C are B,” in which A, B and C are variables that can represent anything in reality. Given the truthfulness of the premises, the truthfulness of the logical outcome should be certain. A logic student could use the power of logic to relieve the burden on the mind. Such is the power of formality by separating contexts from the structure of logical reasoning.

However, there is no way to prove the truthfulness of the premises without falling into infinite regress. Therefore, Aristotle established the theory that intuition gave us the axioms, the self-evident truth as the starting premises, the logic rules, and the other first principles. The rest of the truths were to be either collected inductively, or derived deductively, or logically, and he disproportionately devoted most of his efforts to the latter. He inspired generations of thinkers to transform logical reasoning in the mind to symbol manipulation with pencil and paper, and eventually to calculations using the computer.

Euclid: The Demonstration of Logic

There was a famous inscription on top of the gateway to Plato’s academy:

Let no one who is ignorant of geometry enter here.

Aristotle’s students might find that logic works empirically in real-life arguments, but winning an argument is not necessarily the same as standing with the truth. How about if there were self-evident truths known as the axioms, selected and identified with intuition, from which further truths could be derived according to logical reasoning? Euclid, Greek mathematician 325–270 BC, demonstrated that the known geometrical knowledge could be explained systematically using Aristotelian logic in his timeless and peerless Element. He not only established the discipline of geometry, but also demonstrated a framework of knowledge development from logical reasoning. There are challenges to this framework:

1. How do we identify self-evident truths as the axioms?
2. How can we be sure that the axioms do not use derived truths, causing circular or self-referential arguments?

On the one hand, Euclid successfully showed that the power of logic could be used to demonstrate all known geometric truths up to that time. On the other hand, by being able to logically organize all the previously discovered truths, he also reflected the splendor of intuition, the outcome of which turned out to be “logical”.

This logical framework for mathematical development later encountered obstacles. First, the axioms are not always consistent with reality. For example, it was found that the axioms of Euclidean geometry do not work for physical space on a cosmic scale, where space is curved by gravity according to Albert Einstein’s General Relativity theory. Second, mathematicians would find themselves strangled with self-references despite the efforts to avoid them.

Leibniz: Logic as Calculation

Two millennia later than Aristotle and Euclid, Gottfried Wilhelm (von) Leibniz 1646–1716, a German polymath and big fan of Aristotelian logic, co-invented calculus with Newton. In Leibniz’s time, the way of doing mathematics, by manipulating symbols in place of numbers in algebraic expressions, had matured. We no longer need to list every number of a changing quantity, such as the distance of a moving object, which instead can be represented as an algebraic expression.

Leibniz considered the problems of finding the speed from the varying distances and or the distance from varying speeds. To calculate the speed at any point in time, we need to divide the infinitesimal change in distance by the infinitesimal change in time. Similarly for distance, we need to accumulate every infinitesimal change in distance by multiplying the speed by the infinitesimal change in time. The first calculation is called differentiation and the second is called integration. In either case, we need to use a method called limit process to determine the exact expression when the infinitesimal quantity is arbitrarily close to zero (but not zero).

The left-hand sides of the above two equations are Leibniz’s symbols for differentiation and integration, respectively. Using them, calculus became much easier to learn and understand as opposed to applying limit processes. Originally from Leibniz’s insight, the idea of infinitesimal quantities, that something is almost zero but not zero, was later replaced with a more rigorous definition. Leibniz showed a great example of how intuition works as a scout, or an explorer, to expand the frontier of knowledge.

Leibniz found his differential and integral symbols were unlike other symbols for representing arbitrary quantities, in that they had special meanings, which worked powerfully. This finding gave him the idea of a set of symbols, or an “alphabet”, and a resulting language, to represent Aristotelian logic. He envisioned this new Logical Calculus to render logical reasoning as calculation.

Boole: Logic as Algebra

George Boole, an English mathematician, 1815–1864, who would follow Leibniz’s vision, discovered that logic can be represented as a special kind of algebra called Boolean Algebra. He used algebraic variables for the ones Aristotle used to represent propositions in logic. A Boolean variable takes only 0 and 1 as its values, with 1 standing for TRUE, and 0 standing for FALSE. Likewise, the algebraic operations “addition” and “multiply” represent the logical “OR” and “AND”, respectively. A Boolean variable x refers to a preposition or a class, and we have x²=x, x+1=1. Taking “All men are mortal” as an example, if we use x to represent all men, and y to represent being mortal, then the above sentence can be shown as xy=x. Boolean Algebra made logic a branch of mathematics, advancing one step closer to fulfilling Leibniz’s dream of “logic as calculation”. Today, Boolean Algebra fundamentally underpins the operations of modern computers.

Frege: A Crack in the Foundation

Instead of making logic a branch of mathematics, Gottlob Frege, a German mathematician 1848–1925, chose the opposite approach by turning mathematics into different branches of logic, which he saw as more fundamental than mathematics. So, he used a sophisticated symbolic language to define logic without mathematics. With Frege’s symbolism, all logical reasoning that typical mathematicians would use in his time could be represented as strings of symbols, with no ambiguity. His work was a precursor to modern first-order logic, which embodies elementary logic of (and), (or), (not), (implies), (for all), and (there exists). For example, the following reasoning

All dogs are mammals,

Therefore, the tail of a dog is the tail of a mammal

can be represented as

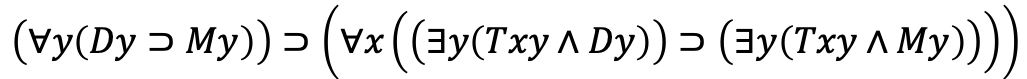
in modern first-order logic, where D, M,T denote “Is a dog”, “is a mammal”, and “is the tail of”. A human reader would find the symbolic version of the reasoning much harder to comprehend. The point is that by representing any logical reasoning as syntactic operations in a symbolic language, its validity could be checked by some kind of “mechanism”. Frege literally established meta-mathematics, in which mathematical proofs themselves could be studied.

Frege tried to rebuild arithmetic, or number theory, that said:

1. To avoid self references, the axioms were based on logic, and the concepts of set.
2. There was no reference to numbers until they were defined from the axioms.

Frege considered the concept of sets more self-evident than that of a number, which was defined as a certain property of sets. You may be tempted to say that this specific property, called “cardinality” of a set, is the “number” of the members in it. But remember, a “number” has not been defined yet. What we can say is that if you can find a one-to-one correspondence between the members of two sets, then they share the same cardinality. Your ideas about numbers learned from your prior experience cannot be counted in Frege’s number theory.

Frege’s game plan was that after showing all known number-theoretic truths could be derived from his axioms and logical rules, all branches of mathematics could be re-established on a logical foundation.

His ambition almost succeeded before meeting a deadly blow. The liar’s paradox kills Norman, the aforementioned fictional android in StarTrek. Similarly, a self-referential paradox ended Frege’s mathematical ambition. Bertrand Russell, an English polymath and mathematician 1872–1970, sent a letter to Frege just before he was about to publish his final and greatest work on logic. In the letter, Russell brought up a scenario simply expressed in Frege’s own symbolic languge:

Given a set that is the set of every set that does not belong to itself, does such a set belong to itself?

This scenario turned out to be a paradox. Assuming it belongs to itself, it does not belong to itself. On the other hand, if it does not belong to itself, then it belongs to itself. Either answer leads to a contradiction. Frege perceived this paradox as a crack in the mathematical foundation that he had planned to secure. Shaken by the fallibility of intuition in general, which he tried to get rid of, Frege despaired and abandoned his work.

Bibliography

• Aaronson, S. (2016). P=?NP. In Open Problems in Mathematics. Springer.
• Aristotle ‘On Rhetoric’: A Theory of Civic Discourse (G. A. Kenndy, Trans.). (1991). Oxford University Press.
• Bansal, K., Loos, S., Rabe, M., Szegedy, C., & Wilcox, S. (2019).HOList: An Environment for Machine Learning of Higher-Order Theorem Proving. Proceedings of the 36th Conference on Machine Learning.
• Bansal, K., Szegedy, C., Rabe, M. N., Loos, S. M., & Toman, V. (2020, June 11). Learning to Reason in Large Theories without Imitation. https://arxiv.org/pdf/1905.10501.pdf
• Borel, E. (1962). Probabilities and Life. Dover Publications, Inc.
• Copland, J. B., Posy, C. J., & Shagrir, O. (Eds.). (2013). Computability: Turing, Gödel, Church, and Beyond (Kindle ed.). The MIT Press.
• Heule, M. J. H., Kullmann, O., & Marek, V. W. (2016). Solving and Verifying the boolean Pythagorean Triples problem via Cube-and-Conquer. In Lecture Notes in Computer Science (pp. 228–245). Springer International Publishing. 10.1007/978–3–319–40970–2_15
• Poincare, H. (1969). INTUITION and LOGIC in Mathematics. The Mathematics Teacher, 62(3), 205–212.
• Polu, S., & Sutskever, I. (2020, September 7). Generative Language Modeling for Automated Theorem Proving. arxiv.org. https://arxiv.org/abs/2009.03393
• Polya, G. (1954). Induction and Analogy in Mathematics.
• Polya, G. (1954). Mathematics and Plausible Reasoning. Martino Publishing.
• Polya, G. (1973). How to Solve It (Second ed.). Princeton University Press.
• Selsam, D., Lamm, M., Bunz, B., Liang, P., Dill, D. L., & de Moura, L. (2019, March 12). Learning a SAT Solver from Single-Bit Supervision. https://arxiv.org/abs/1802.03685