Einstein

Length Contraction in Einstein’s Theory of Relativity

Why Moving Objects are Shortened

Marco Tavora

Dec 10, 2020 — 4 min read

Length contraction is the relativistic phenomenon where the length of a moving object is measured to be shorter than in its rest frame. It occurs only in the direction of motion, and its effect is significant only when the object is moving at speeds close to the speed of light.

The Miracle Year

In 1905, while still working as an assistant examiner at the Federal Office for Intellectual Property in Bern, Albert Einstein published four revolutionary papers in the scientific journal Annals of Physics (Annalen der Physik). In our article, we will be interested specifically in one of those papers, namely, On the Electrodynamics of Moving Bodies (originally entitled Zur Elektrodynamik bewegter Körper) where Einstein introduced his special theory of relativity. In order to reconcile Maxwell’s equations of electromagnetism and mechanics as it was known at the time, Einstein had to introduce revolutionary changes in Newton’s concepts of space and time.

Figure 1: Einstein and page of his special relativity paper where he introduces the Lorentz contraction using Lorentz transformations (see below) (source).

The Postulates of Special Relativity

In one of my recent articles, Why Clocks in Motion Slow Down According to Relativity Theory, (see below) I enunciated the two postulates of special relativity. To keep this article self-contained I will repeat them:

Principle of relativity: No experiment can be performed, which measures an observer’s absolute velocity. In other words, any experiment conducted by an observer will not depend on his speed relative to the other observers.
Universality of the speed of light: The speed of light relative to any observer is constant (and usually denoted by c), independently of the relative motion between the light source and the observer.

Why Clocks in Motion Slow Down According to Relativity Theory

To make measurements on spacetime, Einstein idealized a grid of clocks and rods, like the one below:

Figure 2: Idealized grid of rods and clocks used by Einstein in his thought experiments (source).

Length Contraction

Consider a railroad car moving with velocity v as in Fig. 3 below. The car contains a lamp and a mirror. Clearly, for an observer inside the car, the signal takes

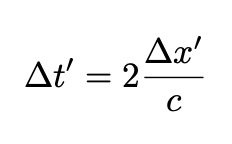
Equation 1: Time interval for an observer inside the car (proper time).

to bounce in the mirror a complete a round trip. The prime indicates time measurements made by an observer inside the train.

Figure 3: A railroad car moving with constant speed v (based on source).

An observer outside the car measures the time it takes for the light to arrive at the mirror:

Equation 2: The time it takes for the light to reach the mirror.

and to return:

Notice the minus sign in the second term, since the train is moving and therefore, the light must move a smaller distance in its return.

The total reflection time for the observer outside is then:

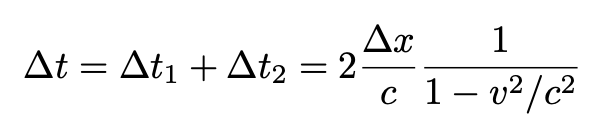
Equation 4: The total time the light takes to reflect on the mirror and return, according to the outside observer.

Using the equation for time dilation

Equation 5: Time dilation (see my previous article).

we obtain straightforwardly:

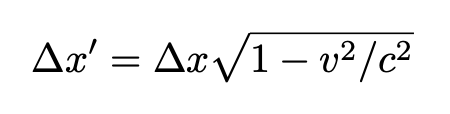
Below, an example of length contraction is shown. In general, at the point where a rotating wheel touches the ground, the velocity v of the contact point must be zero, otherwise, the wheel would be slipping. The length contraction occurs in the upper part of the wheel, where v >0. The animation in Fig. 5 clearly illustrates the occurrence of Lorentz contraction.

Figure 4: At the above portion we have maximum rotation while at the lower portion we have minimum rotation (source).

We conclude that Δx < Δx’: the observed outside measures distances to be smaller.

Figure 5: A relativistic wheel gives an example of length contraction. At the point where the wheel touches the ground, the velocity of the contact point must be zero (otherwise, the wheel would be slipping), and therefore, there is no length contraction. The contraction occurs at the top of the wheel where v>0 (source).

It is also straightforward to derive Eq. 6 using Lorentz transformations in analogy to what we did in this previous article.

Thanks for reading and see you soon! As always, constructive criticism and feedback are always welcome!

My Linkedin posts, my personal website www.marcotavora.me, and my Githubprofile have some other interesting content about physics and other topics such as mathematics, machine learning, deep learning, finance, and much more! Check them out!