Laplace’s Equation

We now come to the third of the most common partial differential equations in physics, Laplace’s equation:

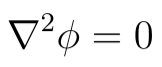
The symbol ∇² is called the Laplacian operator:

I’ve written about Laplace’s equation before in the context of the relaxation algorithm, which is a method for solving Laplace’s equation numerically. Now it’s time to talk about solving Laplace’s equation analytically.

The study of the solutions of Laplace’s equation and the related Poisson equation ∇²ϕ=f is called potential theory. This is because these equations arise naturally in the context of conservative vector fields, meaning vector fields which can be written as the gradient of a scalar function called the potential.

Potentials and conservative fields

Conservative vector fields take their name from conservative force fields, meaning force fields in which the total amount of work that must be performed to move a particle from point A to point B in the presence of the force field does not depend on the path taken from A to B. An equivalent definition is that a force field is conservative if no net work is performed when a particle is moved along any closed path in that field.

Let F be a conservative vector field, let C be any closed path, and let dl be the differential length element of C in the tangent direction to C at each point. Then:

Let S be any surface whose boundary is C and let da be the differential area element vector in the direction normal to the surface. Stoke’s theorem says that:

Therefore:

This must be true for any choice of the path C and any choice of the surface S and this can only be the case if ∇×F=0. So if F is a conservative force field then ∇×F=0. The converse is also true. Assume that ∇×F=0, then for any choice of Sand C:

So a force field F is conservative if and only if ∇×F=0. An important fact is that the curl of a gradient is always zero. Consider just the x-component of ∇×∇f for some scalar function f:

The last line is because of the equality of mixed partials. The proof for the other two components is the same. This suggests that we might try to write a conservative vector field as the gradient of a function, though first we need to prove that such a function exists.

Let C be any path between from point A to point B, let F be a conservative force field, and let U(A) and U(B) be the particle’s potential energy when it is located at point A and point B. By the work-energy theorem, W=U(A)-U(B) so:

Since the work only depends on A and B, we can write this integral as:

Then by the fundamental theorem of calculus, we can write:

Let t be the tangent vector to C so that dl=tdl. Then:

Parameterize the curve with r(l)=[x(l),y(l),z(l)]. Then from the definition of the tangent vector:

Now expand dU/dl by the chain rule:

Then finish by plugging this into F∙t=-dU/dl:

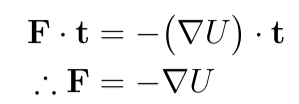
So if F is a conservative force field, then F can be written as a gradient.

Although this has all been in the context of mechanical work, the same result is true for any vector field V regardless of whether V is a physical force field. So for any vector field V, the following statements are all exactly equivalent:

• V is a conservative vector field
• The line integral of V from point A to point B does not depend on which path is taken
• The line integral of V around any closed path is zero
• ∇×V=0
• V can be written as the gradient of a scalar function called the potential

Although there are simple physical problems where it may be possible to calculate V directly, usually we are not that lucky and it will instead make more sense to find the potential and then compute V by taking the gradient of the potential. This is the purpose of Laplace’s equation.

Laplace’s equation

Although we may not know V, it is very common that we know at least something about its divergence. The prototypical example is Laplace’s equation for the electrostatic potential, which follows immediately from Gauss’s and Faraday’s laws:

Since∇×E=0 we can write E=-∇ϕ where ϕ is called the electrostatic potential. We take the negative gradient so that the electric force has the correct sign. Then we plug this into Gauss’s law (the first equation) to obtain Poisson’s equation:

If the potential is caused only by charges located at the boundary or outside of the region of interest then ρ=0 and the potential obeys Laplace’s equation ∇²ϕ=0.

The other major example occurs in the study of incompressible and irrotational fluid flows. Let V be the velocity field of the fluid and let ρ be its density. All fluid flows obey the continuity equation:

Physically, the continuity equation means that the amount of fluid at a point can only change when fluid flows into our out of that point.

A fluid is called incompressible when its density is constant. For incompressible fluids, ∂ρ/∂t=0 and ρ can be factored out of the divergence and cancelled out, so the continuity equation reduces to ∇∙V=0.

In my article about the Navier-Stokes equations, I discussed how a fluid can be described as an infinitesimally small parcel of fluid at each point and the motion of each parcel of fluid can be decomposed into a combinition of a pure translation, a pure rotation, and a pure deformation:

The vector ω represents the rotational motion of the fluid parcel:

Where u, v, and w are the components of V in the x, y, and z directions respectively. This means that ω is just 1/2 times the curl of V. If this quantity is zero then it means that there is no rotational motion, so ∇×V=0 for irrotational flows. This means that the velocity vector field is conservative so we can write V=∇ϕ for some function ϕ. As a minor grammatical point, keep in mind that the flow is irrotational and the velocity field is conservative. Since ∇∙V=0 for an incompressible fluid, this means that the potential obeys Laplace’s equation.

Since irrotational and incompressible flows can be described in terms of a potential, they are often called potential flows.

General solution

The strategy for solving Laplace’s equation will be the same as the strategy that we used for the heat and wave equations: find a complete set of orthogonal functions and then find the coefficients either by taking inner products or some other method. For simplicity we will stick to the two-dimensional case, but everything that will follow is also valid in three dimensions.

We will also handwave away the formal proof of existence and uniqueness with a physical argument. A harmonic potential is a physical field and the configuration of a physical field is determined by the sources of that field. Since sources always create a field, a solution to Laplace’s equation exists. The laws of physics say that the same configuration of field sources cannot produce two or more different fields, and the way that the configuration of sources determines the field is by setting the boundary conditions (since we are assuming that the sources are at the boundary), so the solution to Laplace’s equation is unique. So for any physically reasonable set of boundary conditions, a solution to Laplace’s equation exists and is unique.

With that out of the way, we will now find the general solution. As usual, we use separation of variables. Assume that ϕ=X(x)Y(y). Then:

Since X and Y are single-variable functions, the partial derivatives reduce to ordinary derivatives. Now divide through by XY:

Since X″/X and Y″/Y are each functions of a different variable, their sum cannot be identically zero unless each is equal to a constant:

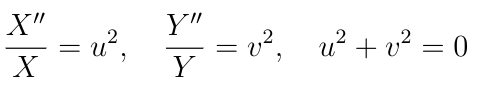
Since ϕ is a physical field, it must be real-valued and therefore u² and v² must be real numbers, although the condition that u²+v²=0 obviously requires that one of the constants u and v is real and the other is imaginary. The eigenfunctions are:

So the general solution is:

We do not necessarily assume that u and v are discrete, so this sum may turn out to be an integral.

We will also find the general solution in polar coordinates. Note that the Laplacian in polar coordinates is:

Assume that ϕ(r,θ)=R(r)Θ(θ). Then after expanding the derivatives, dividing by RΘ, and rearranging, the result is:

The left-hand side is a function only of r and the right-hand side is a function only of θ so the only way for the two functions to be identically equal is if they are both equal to the same constant k:

We are free to choose k however we want, and it turns out that the eigenfunctions take a particularly nice form when we take k=n²:

As for the radial part, the differential equation is a second-order Cauchy-Euler equation:

So the general solution is:

Demonstration: A charged patch on a conducting plate

Two very large (essentially infinite) parallel conducting plates are grounded and separated by distance d. A square patch on one of the plates has side length 2a and is held at constant potential V. Let’s find the potential between the plates.

The general solution is:

The potential should go to zero as x goes to infinity so A₀=0 and the potential should be zero outside of the region between the plates so C₀=0, and since potentials are only defined up to an additive constant we can assume that the remaining constant term B₀D₀ is also zero. This leaves:

Since the boundary condition is an even function of x, ϕ must be an even function of x as well, and we can achieve this by setting Aᵤ=Bᵤ. Then Aᵤ can be factored out of the x part and the constants can be re-labelled:

Remember that exactly one of u and v is real and the other is imaginary. If u is real then the x part of the function will be unbounded as x goes to infinity, which is not allowed. Therefore u must be a pure imaginary number, u=ip, and v is a real number. This leaves us with:

For neatness, we’ve absorbed the 2 in eⁱᵖˣ+e⁻ⁱᵖˣ=2cos(px) into the Aᵤ coefficient. Now we can set v=p since u²+v²=0 and u=ip, so the sum reduces to:

Now we need to use the boundary conditions to find aₚ and bₚ. We can start by writing the boundary condition at y=0 in terms of the Heaviside function:

So the boundary conditions are:

These boundary conditions don’t give us a clear path forward. Fortunately there’s a trick we can use to get around this: the method of images.

Let’s consider the potential field that would be produced if the upper plate was absent:

Suppose that we know the solution ϕ, and suppose that we reflect this system across the dashed line:

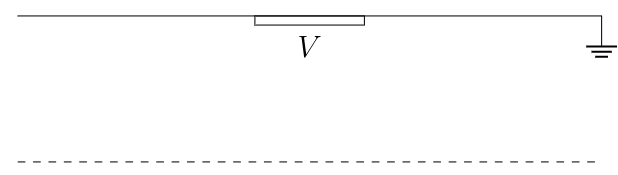
It’s intuitively obvious that the solution for this flipped system will just be ϕ flipped upside-down. Call this flipped solution ϕᶠ. By symmetry, ϕᶠ=ϕ on the dashed line. If we now replace V with -V in the flipped system, then the only effect that this has is to replace ϕᶠ with -ϕᶠ. Although this can be proven mathematically, the easiest way to understand why is to think about the physics. If the patch is at potential +V then the force exerted on a positive test charge is exactly the same as the force which would be exerted on a negative test charge of equal magnitude when the potential is -V. This means that changing the sign of the patch’s potential only changes the sign of the resulting electric field, so the only effect that this has on the potential is to change its sign.

This means that if we combine the original system and the flipped system with the sign of the potential reversed, then the potential on the dashed line will be zero:

This system is equivalent to the original one, and this is the basic idea behind the method of images: given a system of potential sources near a grounded conducting surface, it may be easier to analyze an equivalent system where the surface is deleted and the condition that the potential is zero on that surface is satisfied by inserting fictitious sources, which are called the “images” of the original source.

Now we have an equivalent set of boundary conditions with a more convenient form:

We’ll use these two boundary conditions to get two equations in the two unknown variables aₚ and bₚ:

First we eliminate bₚ:

Then we simplify the sum for ϕ(x,0):

The term in the brackets is just a function of p so we can absorb it into the aₚ coefficient. Therefore:

The function on the right-hand side is not periodic and the domain is the entire real line, so the Fourier series will actually be an integral, and aₚ will be a continuous function of p. So now we have:

Fortunately there’s a continuous version of the orthogonality rule from the discrete case:

The δ(p-q) function is the Dirac delta function, and it is defined by the sampling property:

Now we can find a(p):

Now we’ve found the coefficients:

The solution is:

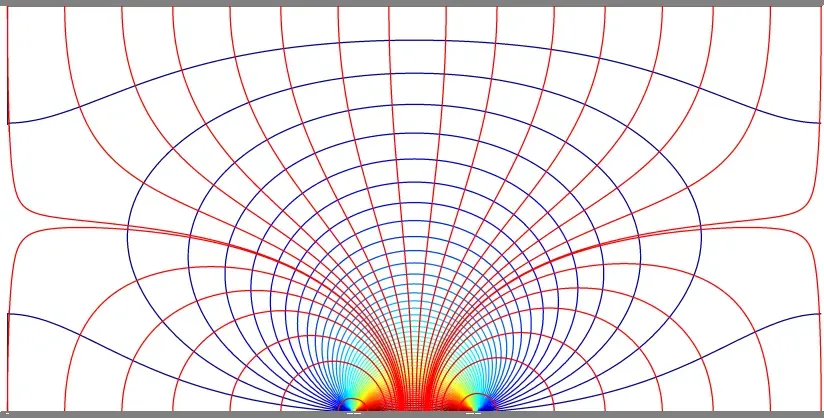
Integrals involving terms like sin(ap)/p are called sine integrals, and it is not possible to compute integrals of this type in terms of elementary functions, so we will just leave this as is. Fortunately this is a very easy problem to solve numerically with the relaxation algorithm, so it won’t be difficult to see what the solution actually looks like. The result is pictured below, and also at the top of this article:

The two plates are at the top and bottom of the image and the patch is in the center of the bottom plate. The plot shows the contour lines of the potential, with warmer colors indicating a higher potential. The electric field lines, in red, are superimposed on top of the contour plot. Field lines go out from the potential patch and terminate on one of the plates. The sharply curved field lines at the sides of the graph aren’t an artifact, by the way. They look that way because that’s where the field lines go from returning back to the lower plate to going to the upper plate.

Demonstration: Potential flow around a cylinder

The potential flow around a circular cylinder is one of the elementary problems in potential theory.

Consider a cylinder of radius a centered at the origin with its axis perpendicular to the xy-plane. An incompressible, inviscid fluid flows towards the cylinder from the left with uniform velocity V₀=u₀x. We want to analyze the flow in the vicinity of the cylinder. We will find the velocity of the fluid by finding the potential and then taking its gradient. Let’s start, as usual, by finding our boundary conditions.

At points very far from the cylinder, the velocity should be V₀=u₀x, so the potential should limit to ϕ₀=u₀x very far from the origin. In polar coordinates, this is ϕ=u₀rcosθ. This might seem to violate the requirement that the potential should be finite everywhere, but from a physical point of view what we’re doing here is assuming that the sources of the flow are at a finite distance away from the cylinder that is still great enough that the presence of the cylinder has no significant effect on the motion of the fluid in the vicinity of the sources. In any event, our first boundary condition is that when r is much greater than a, the potential limits to u₀rcosθ.

No fluid passes through the cylinder’s boundary, so the component of the flow’s velocity perpendicular to the boundary surface is zero. The normal vector is the radial unit vector so r∙V=∂ϕ/∂r=0 when r=a.

When r is very large, the r⁻ⁿ terms in the general solution all vanish, leaving:

To make this equal to u₀rcosθ we’ll have to set a₀=b₀=c₀=d₀=0, aₙ=0 for all n>1, leaving:

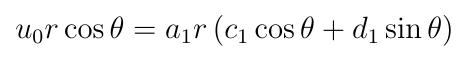
So we’ll have to set a₁c₁=u₀ and d₁=0. Plugging this all back into the general solution and setting Aₙ=bₙcₙ and Bₙ=bₙdₙ leaves:

This will lead to a velocity field whose radial component is:

If we set A₁=u₀a² and Aₙ=Bₙ=0 for all n>1, then ∂ϕ/∂r will be equal to zero for all θ when r=a. Therefore the solution is:

The velocity is just the gradient of this function. The velocity vectors are graphed below:

The contour plot in the background of the vector plot is a graph of the pressure.

The following is an animation of the flow itself, with the streamlines and pressure also pictured:

Copyright stuff, etc

I have given credit for any content that is not my own original work, and I am using that content here under fair use guidelines. The problem in the first demonstration is a modification of one that appeared in the textbook Modern Electrodynamics by Zangwill (2013).