Kepler’s Laws of Planetary Motion

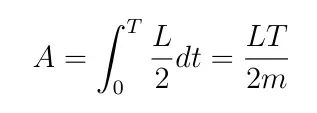
Between 1609 and 1619, Johannes Kepler used data collected by Tycho Brahe to deduce the laws that determine the motion of the planets around the sun:

• Every planet moves in an elliptical orbit with the Sun at one of the foci.
• The planet moves in its orbit, a line drawn from the Sun to the planet will sweep out equal areas in equal times.
• The square of the period of the orbit is proportional to the length of semi-major axis of the elliptical orbit.

These three laws are now named Kepler’s laws in his honor.

This was a surprise to the astronomers of the time, since the Copernican model in which the planets follow perfectly circular orbits was still widely believed. The connection between astronomy and physics had not been made yet, so for mystical and spiritual reasons it was believed that the planets should move in circles, since circles were believed to be perfect shapes and the heavens were the domain of divine perfection. The explanation came in 1687, when Isaac Newton published his famous book Philosophiae Naturalis Principia Mathematica, which provided, among many other great discoveries, the connection between astronomy and physics by using his theory of forces and accelerations to derive Kepler’s laws mathematically.

Although the Principia is worth reading for its historical value, it can be a very difficult book for modern readers to understand because it was written before the development of many important ideas like vector analysis, the concept of a function, the theory of differential equations, and even analytic geometry (which was known in Newton’s day) is used very sparingly and only indirectly when it is used. Therefore this article will present Newton’s proofs in a modernized form.

Equations of motion

We will derive Kepler’s laws from the equations that govern planetary motion. As always, we start with Newton’s second law F=ma. The force is:

In this equation, G is the universal gravitational constant, Mₛ is the mass of the Sun, m is the mass of the orbit planet, r is the distance from the planet to the Sun, and the r-hat symbol is the unit vector for the radial direction. We use a polar coordinate system (r,θ) where the Sun is at the origin. We will assume that the Sun’s motion due to the attraction towards the orbiting planet is negligible.

This means that planetary motion is a specific case of what is called central force motion. A central force system is any mechanical system where the force acts entirely in the radial direction and its magnitude depends only on distance from the origin:

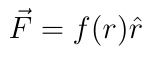
Now we’ll write the components of the acceleration in our polar coordinate system:

A dot written above a variable means the derivative of that variable with respect to time, and two dots means the second derivative. Now we obtain the equations of motion from Newton’s second Law:

Then we obtain the equations of motion by equating the components of the vectors on each side of the equality. They are:

As you can see, this system of equations is badly nonlinear. Attempting to solve them explicitly would simply be a waste of time, so we will need to take a smarter approach to figuring out what these equations are trying to tell us.

The first thing we’ll do is plug m back into the second equation, and notice that:

But the quantity on the left-hand side of this equation is equal to zero, and this means that mr²θ̇ does not depend on time. You may recognize mr²θ̇ as the expression for the angular momentum of a particle of mass m at a distance r from the origin with angular velocity θ̇. This means that angular momentum is conserved. In fact, angular momentum is always conserved in central force motion because force is the derivative with respect to time of momentum, and in central force motion the force has no angular component. This also follows directly from Noether’s theorem.

So the angular momentum equation is:

Therefore we can re-write the equations of motion:

As it stands, these equations are still too difficult for us to solve for time. But fortunately, we don’t have to. We only want to know the shape of the orbit, so all we need to do is find r in terms of θ. As a first step towards doing this, let’s substitute u=1/r. Then let’s use the chain rule to re-write the time derivatives as derivatives with respect to θ:

And then we plug in the angular momentum equation to obtain:

Now we’ll use the chain rule again to get the second time derivative of r:

By substituting the equation for θ̇ in terms of r and L into the first equation, and then replacing r with 1/u and d²r/dt² with the formula we just found, we obtain a differential equation for the path:

The solution is elementary but we’ll save that for the next section.

Finally, notice the force can be written as the negative gradient of a potential:

This means that the force is conservative, so the total energy of the orbital motion does not change with time. The total energy is given by the sum of the kinetic and potential energies:

We are now prepared to derive Kepler’s laws.

Kepler’s First Law

Kepler’s first law says that the shape of the planetary orbits is an ellipse with the Sun at the center. To prove this, let’s start with our differential equation for the shape of the path in the case of central force, inverse square motion:

From elementary differential equations, the solution is:

By using trigonometric identities and substituting u=1/r and α=L²/GMₛm², we can re-write the solution as:

This is the equation for a conic section with the origin at one of the foci. The parameter e is the eccentricity and θ₀ is the angle between the semi-major axis and the x-axis. These terms will be explained in just a moment.

Strictly speaking, this is enough to consider the first law proven since we assumed the Sun is at the origin, but some more detail will be helpful with actually interpreting this result.

A conic section is a curve obtained by intersecting a cone with a plane, and this curve can be an ellipse, a parabola, or a hyperbola:

The eccentricity e is what determines exactly which type of conic section the path of the motion will follow. If e<1 then the path is a closed elliptical orbit, including possibly a circle if e=0. If e=1 then the particle escapes from the gravity on a parabolic path. If e>1 then the particle escapes on a hyperbolic path. If e is infinite then the path is a straight line.

Any conic section defines two perpendicular lines called the semi-major and semi-minor axes and two points called the foci. For an ellipse, these are simply the long and short axes through the center:

The points F₁ and F₂ are called the foci of the ellipse. They are always located on the major axis such that the center of the ellipse is the midpoint of the line segment F₁F₂. The semi-major and semi-minor lengths a and b are the greatest and least distances from the center to the perimeter of the ellipse. The eccentricity is defined in terms of these lengths.

The focal points are both at a distance of ae from the center of the ellipse. The apoapshis and periapsis of each focus are the points that are closest and furthest away from each focus. The apoapsis length is a(1-e) and the periapsis length is a(1+e) (remember that e<0 for an ellipse).

For a hyperbola, the semi-major axis is the line between the apexes of the two branches, and the semi-minor axis of each branch is the perpendicular line from the apex of the branch and the asymptote:

As before, the focal points are at distance ae from the “center” of the pair of hyperbolas, which could be considered as the midpoint of the line segment between their vertices. The eccentricity is defined by:

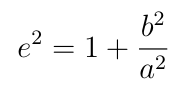
For a parabola, the situation is somewhat different. Recall how a parabola is constructed. We draw a line called the directrix, and then pick a point called the focus. The parabola is the set of all points whose distance from the focus is equal to their perpendicular distance from the directrix:

The focus is at a distance 1/4a along the axis of symmetry from the vertex. The “major axis” in this case is the axis of symmetry.

The condition for whether the shape of the path is an ellipse, a parabola, or a hyperbola is whether the total energy E is negative, zero, or positive, respectively. To understand why, first note that the kinetic energy is strictly positive, because it is a sum of squares, and the potential energy is strictly negative, and remember that the value of E does not change. Then:

• If E<0 then the planet doesn’t have enough kinetic energy to escape from the potential well of the gravitational field so the planet’s distance from the star is bounded. The only path satisfying the equation for r(θ) that satisfies this requirement is that of an ellipse.
• If E=0 then the planet has just barely enough energy to escape and therefore just barely fails to make a closed orbit. The value of the eccentricity for which the path just barely fails to make a closed curve is 1, so E=0 means we have a parabola.
• If the energy is infinite then the planet shoots right past the star in an instant without interacting at all and therefore the path would be a straight line. So if E is between 0 and positive infinity then the curve should be “between” a parabola and a straight line, and the only such curves that satisfy our equation for r(θ) are hyperbolae.

Kepler’s Second Law

Kepler’s second law, also known as the “law of equal areas” tells us that a line from the Sun to the planet will sweep out equal amounts of area in equal amounts of time:

Kepler’s second law requires much less work to prove than the first law. It is also interesting that the second law holds in general for central force motion, unlike the first and second laws, which are true only for the inverse square case.

The area of a sector of an ellipse drawn from one of the foci that subtends an angle φ is:

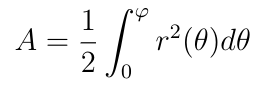
Now we’ll consider the differential elements of each side of this equation:

So dA/dt is constant since L is constant. Therefore the area swept out in time T depends only on T:

This completes the proof.

Kepler’s Third Law

Kepler’s third law says that the square of the orbital period is proportional to the cube of the semi-major axis of the ellipse traced by the orbit. The third law can be proven by using the second law. Suppose that the orbital period is τ. Since the area of an ellipse is πab where a and b are the lengths of the semi-major and semi-minor axes. Kepler’s second law gives:

From the equation for the eccentricity, the semi-axis lengths are related by:

Square both sides of the second law equation and then plug in this result for b²:

Recall our equation for r(θ):

We have dropped θ₀ and we choose a coordinate system in which θ=0 coincides with the apoapsis. The apoapsis length is a(1-e) and by equating this to r(0) we get:

Now we’ll complete the proof by plugging this in to the equation for the period:

Closing remarks and copyright stuff

Isaac Newton’s mathematical derivation of Kepler’s laws was one of the greatest achievements in the history of science. After thousands of years, the question of why the planets move through the heavens as they do, a question which had occupied the minds of philosophers at all stages of history until that point, had finally been answered. In addition to this, it proved that Newton’s theories of universal gravitation and his laws of motion were correct, and silenced once and for all any doubt of the Solar System’s heliocentricity.

I have cited any pictures that are not my own original work. Fair use guidelines protect the use of this material for purposes of reporting, instruction, and criticism.