Is it time to retire Newton’s Gravitational Constant?

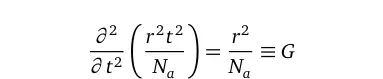
They say no matter how good a dancer you are, you must know when to leave the dance floor. Unfortunately, that doesn’t seem like a pleasant thing to say to a piece of scientific law that has diligently served it’s purpose for nearly half a millennium.

Newton’s gravitational constant (denoted G), has been instrumental throughout the development of the earlier laws of physics, up until the currently accepted form of general relativity. However, recent research advises on the merits of finding alternative theories that fully accounts for gravitation activities in the quantum level. The focus of this essay, is on the problems encountered upon continued use of the constant in its current form. An attempted has also been made, to offer a possible alternative to the constant, while assessing its merits, and ensuring its functionality persists.

Problem description

In Newtonian physics, G is a proportionality constant for the gravitational force acting between two masses. However, in the general relativistic context, it signifies a connection between spacetime geometry, and the energy-momentum tensor proposed in Einstein’s field equations. The problem with both of these theories is they work quite well in macro scales but ultimately collapses when applied to micro and nano systems. For example, we know gravitational acceleration of given body of mass, M, and radius r, is calculated from Newton’s law as follows:

However, when we try to apply for a proton with estimated radius of 0.87687101 femtometers, the law of gravity breaks, and we don’t end up with expected results. The outgoing description is thus one of today’s most counterintuitive topics in the field of theoretical physics. There are two main arguments to support the search for a quantum theory of gravity:

While the other three fundamental forces of physics namely: electromagnetic, the weak, and strong interactions, are founded on quantum field theories, that leaves out gravity for lack of its quantum field counterpart description

Moreover, it is always argued that it is not sufficient to consistently couple a classical to a quantum system¹.

A Closer Look at the Constant G

Anyone who has ever bothered to look at the dimensions of Newton’s universal gravitational constant, would have noticed that it is a concentration number.What does that mean? Well, in the very precise mathematical language, it represents a variation in the reciprocal of density per square second. A pure abstraction from its dimensions (m³/kgs²), suggests that you could easily express it as a continuous function of mass density as follows:

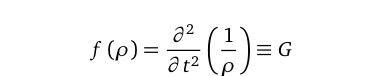
This would be the beginning of a mathematician’s journey, to find the function (of ρ) that satisfies Eq. (2). But an even bigger question arises, as to what does it measure. Rather, the concentration of what? First, lets lay down some truths about G. It turns out that the constant G really is related to Avogadro’s constant Nₐ, in a captivating manner. We usually express the mass density ρ, as a function of number of atoms/particles n, molecular weight m, volume V, and Nₐ as follows.

In deed a detailed analysis of Eq. (3) will result in an elegant relationship showing that the volume (of substance) is expressible as a function of time in the following way:

The assertion that G is a measure of concentration is therefore a valid one, as we see Avogadro’s constant making an entry. But remember we still haven't explained what the concentration measures. This is reserved for the next sections.

Introducing a Mole of Force (molf)

We know that the concentration of anything can be measured in moles. Chemical reactants, and even protons. Joseph John Thomson introduced his a century ago, named “corpuscle” — a charged matter, that we now know as electron². A mole of anything will consist of 6.022×10²³ units, which can be atoms, molecules, or whichever particles. What if we had a mole of force? Would it make things easier? Well, let’s see by first substituting Eq. (4) and (3) in Eq. (2). Solving the resulting differential equation results in the following:

Now that we know what G is in terms of Avogadro’s number, we need to place it where it belongs, substituting Eq. (5) in the Eq. (1) and solving for gravitational acceleration, g.

We are closing in on a significant finding here. If you take the radius of Earth r≃ 6339697.74 m, square and divide by Avogadro’s constant Nₐ, you get the value of G. Similarly, the mass of Earth M≃ 5.90570266840541E24 kg, divided by Nₐ should return Newton’s gravitational acceleration on Earth, about 9.80665 m/s². This is only possible because of the mole force — concept. We therefore have to define the mole of force (molf), as the ratio between the mass (of the planet), Mand it’s gravitational acceleration g, and we can represent it as follows:

The derived units of the molf is kgs²/m.

Benefits of Defining the molf

1. With the notion of the molf, we can now estimate acceleration due to gravity for any particle or object whatsoever, as long as we know the mass. Including both those of subatomic particles such as the electron mₑ, proton mₚ, and even those of cosmological extends such as the Earth as we have seen. All that is done in one formula — provided in Eq. (6).
2. We could then write a more holistic law of gravity such that:

Keep in mind, the masses in Eq. (8) can be any two, e.g. that of a stone and that of Earth, or that of an electron and proton, if you want to estimate the force of attraction between them.

3. Explaining quantum mechanical properties might be easier now. For instance, besides the gravitational acceleration of say protons, I can also write its Schwarzschild radius as follows:

It is important to note that the outgoing operation is not entirely possible with Newtonian mechanics or even general relativity, since the value of G predicted by those models is way exaggerated. For the proton, this model predicts a Gₚ ≃ 1.27678723198924E-54 m³/s²kg. We know this is true, because with a proton radius of 8.76869E-16 m, we can conduct the following operations:

Knowing that the mass of a subatomic particle is given through Compton wavelength, Eq. (10) may be extended to estimate the acceleration due to gravity within the confines of the atomic model as follows:

Where h is Planck’s constant, λ the Compton wavelength (for subatomic particles), and c the speed of light in a vacuum. For larger objects of cosmological extents such as celestial bodies, λ is given as a function of Schwarzschild radius as follows:

The origin of Eq. (12) was explained in another article on extending Einstein’s field equations. To compare the proton mass m, and the mass of Earth, we would then write the following:

Finally, we may write the general equation as:

Conclusion

Mathematical operations that involve Newton’s gravitational constant are extremely counter intuitive at the subatomic level. This is due to the lack of a unified methodology to carry out these calculations. Newton’s constant G, when used in both classical mechanics and general relativity, seems to work excellently, but only within those regimes. However, the logic breaks down when an attempt is given, to the calculations for particles at the subatomic level. With the method described in this essay, we are beginning to see a relation that could draw us nearer to the realms of quantum gravitation. We find that force can also be quantified as a concentration, in a similar way chemical reactants, electrons, and protons are quantified. We defined a mole of force (molf) as the ratio between the mass and gravitational acceleration, such that exactly 6.02214086 × 10²³ particles exists per molf.

References

¹Whitaker, A. (2006). Einstein, Bohr and the quantum dilemma: From quantum theory to quantum information. Cambridge University Press.

²https://www.nytimes.com/1997/04/29/science/finding-corpuscle-of-electricity-shaped-knowledge-of-matter.html