Inverse-Square Law of Gravitation: The Role of the Apple and the Moon

The equation shown above is one of the most famous equations in physics which changed the world forever. It is the mathematical expression of the law of universal gravitation. Here, F is the gravitational force of attraction between two bodies, M₁ and M₂ are the masses of those two bodies, r is the distance between them, and G is the gravitational constant.

There are two parts to the law of gravitation:

The second part, F∝ 1/r², makes it an example of an inverse-square law. Newton was able to confirm this part by using only the radius of the Earth, the radius of the Moon’s orbit around the Earth, and the Moon’s orbital period (which were known in his times). This interesting piece of work is described in his Mathematical Principles of Natural Philosophy. It can also be found in the bookGravity by George Gamow, in a somewhat modernized form. In this story, I discuss the simple mathematics behind Newton’s way of confirming the inverse-square law (in a similar fashion as in Gravity). In addition, I also discuss an alternate way to prove it.

Newton and an apple are intimately connected though there is no solid proof that the falling apple sparked the idea of Universal Gravitation. During the stay at his Lincolnshire farm in the 1600s (the Great Plague time), Newton had a radical idea: the force of gravity which makes the apples fall down is also responsible for making the Moon rotate around the Earth. To support this argument, he did a thought experiment which is known as ‘Newton’s cannonball’. Let’s go through this thought experiment.

Newton’s cannonball

Imagine a cannon at the top of a high mountain, as shown in Fig. 1. When the cannon fires the cannonball, if there were no air resistance and the force of gravitation, it would follow path A, and would never fall on the Earth. However, there is the attractive force of gravitation between the cannonball and the Earth, according to Newton. Hence, the cannonball would follow curved paths B or C depending on the initial velocity of the cannonball.

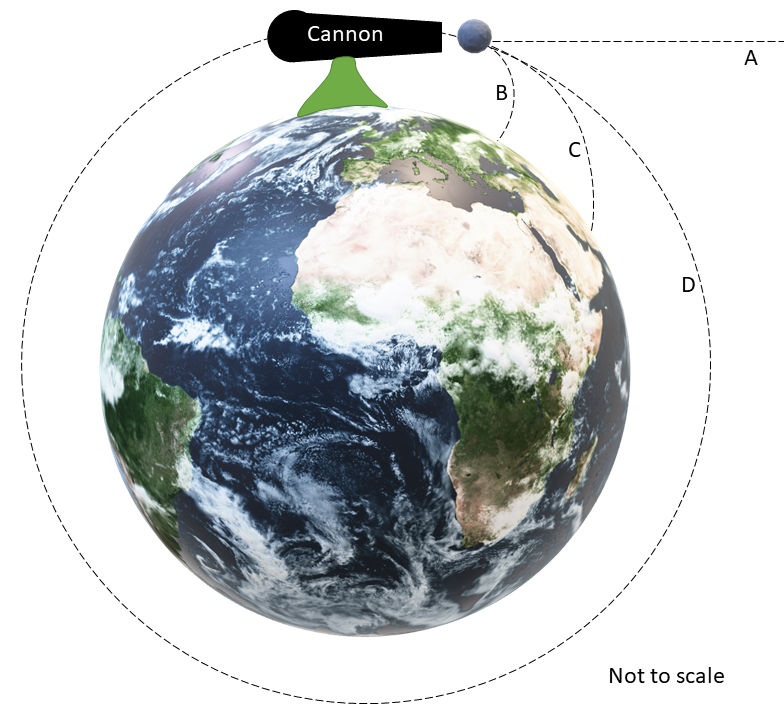
Since the Earth is round, it curves under the path of the cannonball. At a certain limiting initial velocity, the rate at which the cannonball falls towards the Earth equals the rate at which the Earth’s surface curves away from the cannonball. In this case, the cannonball follows path D in Fig. 1. It keeps falling freely towards the Earth but misses it always because the Earth keeps curving away from it. Similarly, the Moon is in free fall towards the Earth but always misses it.

So, using the above thought experiment, how did Newton confirm that the force of gravity between two bodies (e.g. the Earth and the Moon) is inversely proportional to the distance between them? In Newton’s times, as mentioned before, the radius of the Earth (Rₑ), the radius of the Moon’s orbit around the Earth (R), and the Moon’s orbital period (T) were known. He also had Kepler’s laws and Galileo’s work on free-falling bodies at his disposal. Let’s have a look at the thought process Newton could have gone through to confirm the inverse-square law.

Newton’s argument

Figure 2 shows the Earth-Moon system, where the Moon is in a circular orbit around the Earth. At a certain point in time, the Moon is at a location denoted by A. Had there not been the attractive force of gravity between the Moon and the Earth, the Moon would have travelled along the path AB in Fig. 2 (like path A in Fig. 1).

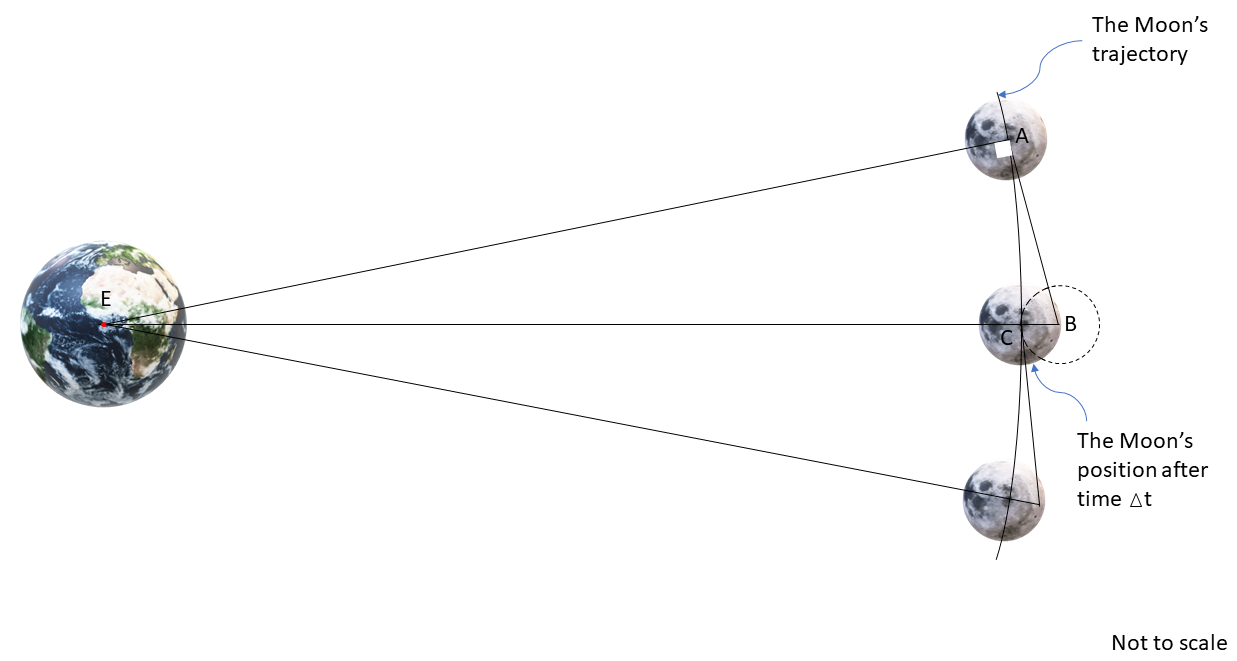
At any moment, the velocity of the Moon perpendicular to EA (radius of the Moon’s orbit) is v. In a short time interval Δt, the Moon would have travelled distance AB (=vΔt). However, because of gravity, it falls towards the Earth by CB. Applying the Pythagorean theorem to a right-angled triangle EAB,

EC = EA. Cancelling these two terms from both sides of Eq. (1) and dividing it by 2EC throughout gives,

As the time interval Δt becomes shorter, CB becomes smaller. CB² tends to zero faster than CB because it is a squared term. For a sufficiently small Δt, CB² can be neglected in comparison to CB, and we get,

We know that AB = vΔt. Representing EC (the radius of the Moon’s orbit around the Earth) as R, CB (the distance covered by the freely falling Moon in time interval Δt) can be expressed as,

According to Galileo’s law of free fall, the distance (s) covered by a freely falling body in time Δt is given by

where a represents the acceleration of the freely falling body. Comparing Eqs. 4 and 5, the acceleration with which the Moon falls towards the Earth is given as a = v²/R. It can also be expressed as,

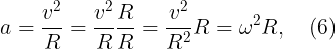
where ω is the angular velocity of the Moon around the Earth. ω can also be written as,

where C (=2πR) is the circumference of the Moon’s orbit around the Earth. But, C/v = T, the orbital period of the Moon. Hence, ω = 2π/T. Since T = 27.3 days (or 2.35 𝖷 10⁶ seconds), ω =2.67 𝖷 10⁻⁶ s⁻¹. Substituting ω and R = 384400 km in Eq. (7), a = 0.274 cm/s². So, at a distance of R from the centre of the Earth, the acceleration due to gravity is less than that at the surface of the Earth (which is represented as g, and g = 981 cm/s²). It means that the force of gravity decreases as you go away from the Earth. But what is the law that governs this decrease?

For an apple falling from a tree on the surface of the Earth, the distance between the apple and the Earth can be taken as the radius of the Earth (Rₑ = 6371 km), and the apple falls at g = 981 cm/s². Similarly, for the freely falling Moon, the distance between the Earth and the Moon can be taken as the radius of the Moon’s orbit (R = 384400 km), and the Moon falls towards the Earth at a = 0.274 cm/s². The ratios g/a and R/Rₑ are 3580 and 60.33, respectively. Newton noticed the following relationship between the two ratios:

Hence, the force of gravity is inversely proportional to the square of the distance between the two objects. The mathematics of this story is simple. However, the genius of Newton lies in proposing that the force which makes the apples fall from a tree on the surface of the Earth is also responsible for keeping the Moon in its orbit around the Earth.

The alternate way!

There is another way to prove the ‘inverse-square law’ behaviour of the law of gravitation. According to Newton’s second law, the force of gravity acting on the moon is given as, F = Mₘ(v²/R), where Mₘ is the mass of the Moon. We know that v = (2πR/T), where 2πR is the circumference of the Moon’s orbit, and T is its orbital period. Hence,

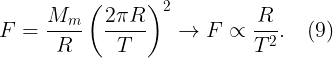
If we know the relationship between T and R on the right-hand side of equation (9), we can confirm the relationship between F and R. Here, Kepler’s third law helps. Mathematically, Kepler’s third law is given as follows: Tₚ²∝ Rₚ³, where Tₚ isthe planet’s orbital period around the Sun and Rₚ is the semi-major axis of its orbit, respectively. This law is also applicable to the natural satellites like the Moon revolving in almost circular orbits around their mother planets. For the Earth-Moon system, if we employ Kepler’s third law, Eq. (9) implies, F∝ 1/R².

Thanks for reading! Constructive criticism and feedback are always welcome!

References

• George Gamow, Gravity, Dover Publications.
• Isaac Newton, Mathematical Principles of Natural Philosophy.