Introduction to the Brachistochrone Problem — Finding the Time to Slide Along a Path

It seems like the most common introduction to the Calculus of Variations is to talk about the Brachistochrone problem. It goes like this.

Imagine you have a bead that can slide along a frictionless wire under the influence of gravity only. You want the bead to slide (starting from rest) from point 1 to point 2 along some path. What path would produce the shortest time?

So, let’s do this.

Bead on a Straight Wire

I’m going to start with the simplest path possible — a straight line. It looks like this.

Oh, why did I pick weird starting and ending points? You will see why soon (hopefully). But here is how to find this sliding time. I’ll start by breaking the path into small pieces — where each piece has a length of ds. I need to find the time it takes the bead to move along this short piece. That time depends on the velocity. So, using the definition of the velocity, I can find the time.

Now that I have the time for each piece, the total time will just be the sum of short times. Of course I will take the limit as dt goes to zero and this will make it an integral.

Clearly, I’m not ready to integrate that function. First, the value for the velocity changes as the bead moves down the line. Second, I need to get ds in terms of dx and dy. Let’s start with ds. If you have a tiny little piece of the track, it will look like this.

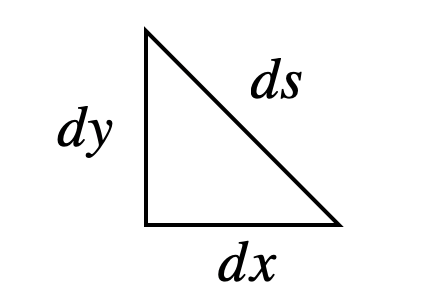
Since dx and dy are perpendicular, this is a right triangle. The length of ds would then be:

I don’t really want to have both dx and dy in this expression — so I’m going to use a trick. I can rewrite dy as:

Yes, I’m calling y’ the derivative of y with respect to x. But that means that ds would be:

But I still need to do something with y’. Here I can use the equation of the path from point 1 to point 2. It’s just a straight line with a slope of -1 and a y-intercept of -1.

So, the derivative of y with respect to x (which is y’) will just be -1 in this case. Great. Now I need to deal with the velocity. For this, I will use the Work-Energy principle. The Work-Energy principle says:

Suppose I have a system consisting of the bead and the Earth. In that case, there’s only one external force on the system — the force from the wire that the bead slides on. However, this force does zero work since it always pushes perpendicular to the path the bead moves on (there’s no friction). That means the total work is zero and the changes in energy will consist of the change in kinetic energy and the change in potential energy.

If the bead starts from rest, then we get the following from the work-energy principle. This for the bead that starts at position 1 (-1,0) and ends up at some value of y (remember, y is negative — so don’t freak out about the square root of a negative number).

I want to put this expression for v into the integral, but not like this. It would actually be better to have this as a function of x instead of y. Oh, that’s fine — I already know how those two are related since the bead is on the line and I already have that equation. I can substitute for y to get the following.

Yes, x is going to be negative, but I’m pretty sure this will give a positive (and real) velocity. Whatever. Let me just put it all together.

That’s the answer. Oh, yeah maybe I glossed over the integration — but I figured you could go back over that and make sure you know what’s going on.

But wait! You can check this answer. If you have a bead going down an incline, (it’s a 45 degree slope) then the acceleration would be:

Also, the total distance would be sqrt(2). You can use the basic kinematics equation to find the time to get to the end of the track. You get the same thing.

But wait AGAIN! I actually did this numerically in python. Why? Because I’m going to need to do this for the next path and I want to be fair. Here is a link to the code and this is what it looks like.

If you print out the time, you get the same as the above calculation (t = 0.638 seconds). Yay.

Bead on a Circular Wire

Let’s do this again. Same starting and ending points, but a different path. It looks like this.

Quick! Do you think this bead will take MORE or LESS time than the straight line bead? Well, let’s find out. Really, the big difference in this case is the equation of the line path. Since this is a circle, I get the following:

First thing is to find an expression for ds — so, I need to get y’. It’s just taking a derivative, so I will let you do that. You should get this.

Now I can put that into my expression for ds:

Second thing is to get an expression for the velocity. It’s the same as before in that it only depends on the y-value, but now there is a different relationship between x and y.

Putting the ds and the v together, I get the following integral for the total time.

Surely I could simplify this — but:

But really, I don’t want to simplify that — I just want to get the time. Oh, I’ll use WolframAlpha (it’s pretty good). Here’s what I get.

That’s a time of 0.592 seconds. OK, I’m cool with that. Also, I know this isn’t the best form because that function is undefined at x = -1. Oh well. I have a time (and it’s a quicker time than the straight line).

But there is another way to check this value. If you the mass is moving down a circular path, then this is the EXACT same situation as a mass swinging on a string (a pendulum). I can model that fairly easily. I’ll skip the details, but here is code. The output looks like this.

From that, I get a total time of 0.5923 seconds. Yeah, I’m pretty happy with that.

Homework

If you want some homework, consider the following:

• What about a parabolic path from point 1 to 2?
• Why can’t you do a circle that curves down instead of up (well, not with the same radius as this one)?
• Now for the fun part. Pick a point at x = -1/2 (in the middle). Vary the y-value for that point so that you have two straight line segments. Find the value of y such that the time is minimized.