These days all your devices are encrypted. Apple boasts about their secure systems, most companies have encrypted servers, even your own laptop probably has some level on encryption going on. However, all of these systems are subject to fault. Of course, this all depends on the type of encryption you’re using. While many agree that the standard is and should be AES, there are a lot of other encryption protocols out there, some of which are still in use today. One of the other main algorithms still circulating the globe is the RSA algorithm. In order to understand why, we have to go back to before its time, to the beginnings of modern cryptography.

In the beginning, there were two…

Known mostly within the American cryptologist worlds, Martin Hellman was the more academic of the two. After having received a Ph.D. from Stanford University in 1969, he joined the teaching staff in the electrical engineering department, where he still teaches today.

The second person was Bailey Whitfield Diffie, who could be considered more of your stereotypical revolutionist. After he had attained a Bachelor of a Science from M.I.T in 1965, Diffie worked as a researcher in Boston and Stanford. After 8 years, and a growing interest in cryptography and computer security, he decided to pursue his research full time with the help of his future wife, Mary Fischer.

In the summer of 1974, Diffie and Fischer met with a friend at the Thomas J. Watson Research Centre in New York, which housed one of the only non-governmental cryptographic research groups in the United States at the time. While the director couldn’t say much due to secrecy orders, he advised Diffie to meet with Hellman, who was teaching at Stanford while also pursuing a cryptographic research team. A planned half-hour meeting between the two turned into many hours of shared ideas and information. In order to continue their blossoming partnership, Hellman hired Diffie under the university as a grant-funded part-time research programmer for the 1975 spring term. For the next year, the pair attended multiple difference conferences on cryptology and even criticized the NBS proposed Data Encryption Standard for potential security risks (including a key length of only 56-bits). Then in 1976, the two first proposed the idea of an asymmetric public-private key cryptosystem. Their system used a shared-secret-key created from exponentiation of some number, modulo a prime number.

Then there were three more…

Despite leaving the problem of realizing a one-way function open, Diffie and Hellman laid the groundwork which would allow others to go down in computer science history.

Two researchers at M.I.T first caught wind of the proposal of a public-private key system and set to the task of discovering the missing ingredient. Ron Rivest and Adi Shamir, along with fellow cryptographer Leonard Adleman, made several attempts over the course of a year to create the proposed “one-way function” required to implement the algorithm. Rivest and Shamir, as the computer scientists, proposed many potential functions, while Adleman was responsible for finding their weakness, as he was the mathematician of the group. They tried many approaches including “knapsack-based” and “permutation polynomials”. For a time, they even thought that what was need would be impossible to obtain due to the conflicting restraints.

Then in April 1977, the trio was spending the night at a students house when Rivest was unable to sleep, and so proceeded to lay on the couch with a math textbook and again begin pondering their one-way function. After an apparent eureka moment, he spent the rest of the night formalizing his idea and supposedly had much of the paper ready by daybreak. When the trio published the paper of the discovery in August of 1977, with the name RSA for the initials of their last names, they tried to patent it throughout the globe. However, since the paper had already been published at the time of application, the United States was the only country to grant the patent for a “Cryptographic communications system and method” in 1983. 17 years later (when the patent expired), the algorithm was officially released to the public domain by RSA Security on September 6th, 2000.

The RSA Algorithm

The RSA (Rivest–Shamir–Adleman) is an algorithm used by modern computers to encrypt and decrypt messages. It is an asymmetric cryptographic algorithm, meaning that there are two different keys that are being used. It also goes by the name ‘public key cryptography’ because one of the keys can be given to anyone, without compromising the system. The other key, a large composite number, is kept private in order to decode the information. The algorithm is based on the fact that finding the factors of a large composite number is difficult: when the integers are prime numbers, the problem is called prime factorization. More specifically, the process for creating your public and private keys goes like this:

1. Choose 2 different large prime numbers p and q (numbers can be verified as prime by primality tests)2. Calculate n = pq | n is used as the modulus for the public and private keys. It's length, usually expressed in bits, is the key length.3. Calculate ɸ(n) = (p - 1)(q - 1) | where ɸ(n) is Euler's Totient function, and since n = pq where p and q are prime, we get this relationship.4. Choose an integer e such that 1 < e < ɸ(n), and e is coprime to ɸ(n) | For two numbers to be co-prime, they must share no factors other than 1.5. Compute d to satisfy the congruence relation de ≡ 1 (mod ɸ(n)) | In order to solve this relationship, you can use the Extended Euclidean Alogorithm.

After having completed these steps, your system would then send out your public key to the world, which would look something like (n=?, e=?) . Using this key, systems wanting to send you an encrypted message would use that information like this:

To send a message M, you would change M into a number m < n using a padding scheme. Then you would compute the ciphertext (encrypted text) c such that c = mᵉ (mod n), i.e the remainder of mᵉ/n and send it to the recipient. This can be done efficiently on computers using exponentiation by squaring. Note that in these steps, n and e are the values of the public key which was shared by the intended recipient.

Now that your message has been encrypted, it can be sent freely around the web, since only the jumbled up ciphertext is actually been transmitted. This is where the one-way function Hellman and Diffie described comes into play. Using the relationship m = cᵈ (mod n), computers can use the Chinese Remainder Theorem to calculate m and obtain the original message, which is possible to do under the exponent d , the private key that only the recipient knows. Here is an example of the RSA algorithm in action:

1. Choose two random prime numbers; p = 61, q = 53.2. Compute n = pq = 61 * 53 = 32333. Compute ɸ(n) = (61 - 1)(53 - 1) = 31204. Choose e > 1 coprime to 3120; e = 17 | Arbitrarily chosen5. Choose d to satisfy de ≡ 1 (mod ɸ(n)); d = 2753 | Solve using the Chinese remainder theoremThe public key is (n = 3233, e = 17). The private key is (n = 3233, d = 2753)To encrpyt m = 123, we calculate c = 123¹⁷ mod 3233 = 855
To decrypt c = 855, we calculate m = 855²⁷⁵³ mod 3233 = 123Note that while I skipped showing the calculations for brevity, both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation.

For those of you who are more mathematically inclined, a full proof is not that hard to build. The namesakes of the RSA algorithm provided a very nice proof along with their proposal of the algorithm, which shows that (mᵉ)ᵈ ≡ m (mod pq). The original proof proposed used Fermat’s little theorem, and while that approach is still valid, many proofs rely on Euler’s theorem instead. There is a proof of the correctness of the RSA algorithm here, which used a combination of modular arithmetic and Fermat’s little theorem to prove the algorithm is always correct, similar to how it was done in the original paper.

What does it all mean

Despite being conceived almost half a century ago, the RSA algorithm is still used in a lot of modern technology. First and foremost, it is used in a lot of hybrid encryption schemes. Often times files get very large, and it would be inconceivable to encrypt the whole file using this kind of system. Instead, the file would be encrypted symmetrically (similar to password protection), and then the key would be encrypted using the RSA algorithm, and both would be sent to the recipient. This allows for much larger files to be securely transmitted over the internet with very marginal encryption and decryption times.

Another crucial place the algorithm shows up is for digital signatures (like that of an SSL certificate). Using the private key, a computer (or person) can sign a message (or file) into an encrypted state. Once the file is sent to the intended recipient, they can use the public key to authenticate the file and verify that it has not been altered or damaged. Since the public key is used to authenticate the file (or message), the verification can theoretically be done by anyone, since the public key is not sensitive information. This is the basis of how digital authentication works, specifically SSL. An authorized provider will sign a certificate with their private key. This certificate is provided to the web client when a website loads, along with the corresponding public key. The client next verifies the certificate using the public key, which authenticates the certificate, the identity of the provider and allows the server that sent the certificate to open a secure connection to the client.

Cracking the code

The main problems that come with an encryption algorithm are reliability and robustness. An algorithm can be the most beautifully complicated thing in the world, but if it can be broken in a short enough timeframe, it is effectively useless. The main technique employed to break the RSA algorithm is one of brute-force. Simply stated, it involves trying all the possible combinations of a private key until you find the right value. While this is trivial for smaller values, when you think about how large prime numbers can get, it becomes a mammoth task. In order to break the RSA algorithm, you would need to find the prime factorization of n, which is provided in the public key. It has become known as the RSA Factoring Challenge. The challenge was put forward almost 30 years ago and has been increasing in difficulty each time a level is completed. To date, the largest key ever to be correctly factored into prime numbers was a 768-bit key, which corresponds to a 232-digit semiprime, by a team of researchers lead by Thorsten Kleinjung. They used the equivalent of almost 2000 years of computing on a single core 2.2 GHz AMD Opteron. Nowadays keys in use in modern systems are at a minimum of 1024 bits, most going up to 2048 bits, so your texts are probably safe. But that could change very soon.

Quantum computing

So what does this have to do with quantum computers? Well, the rise of quantum computing has been worrying to some people, and rightly so. Although the handful of quantum computers that existing today are not very powerful (compared to what they could be), this is mainly because of the practicalities of building and running them. And so, it did not stop mathematicians from coming up with algorithms that could theoretically work on powerful enough (and stable enough) quantum computers, to break modern encryption schemes.

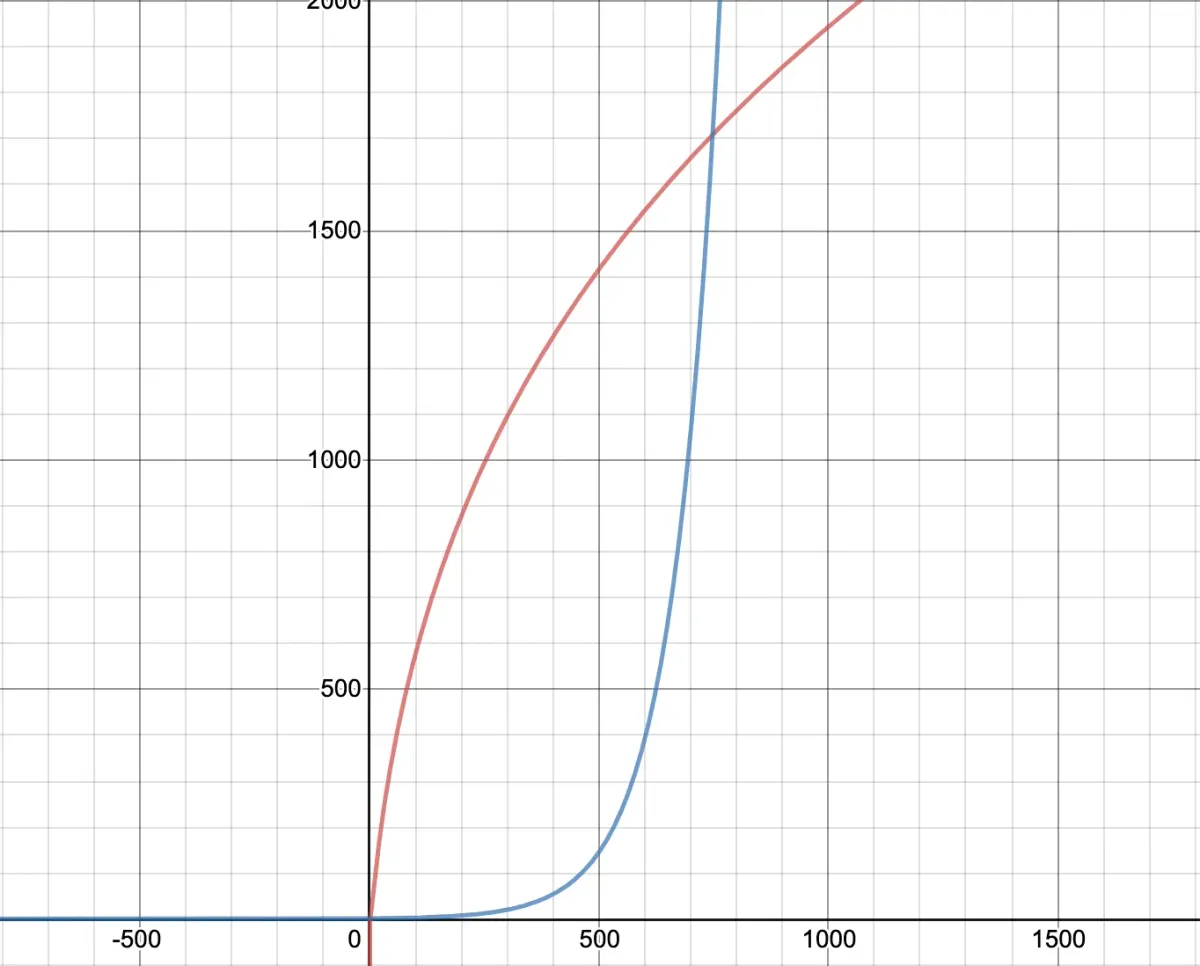
One algorithm, in particular, poses a very real threat to the RSA algorithm. Shor’s algorithm, named after American mathematician Peter Shor, in fact effectively cracks the RSA scheme. Informally, it solves the following problem: Given an integer N, find its prime factors. There are algorithms that run on today’s computers capable of solving this problem, but the fastest one (general number field sieve), only works in sub-exponential time. Shor’s algorithm theoretically works in polynomial time, which is a massive improvement on the former. In layman’s terms, the fastest computational algorithm will increase in speed according to an exponential function, so a larger number to compute results in an exponentially larger runtime. Under Shor’s algorithm, the runtime increases according to a polynomial function, which grows a lot slower when compared to an exponential function. One estimate for the theoretical runtime of the algorithm is 72(log N)³, which when compared to even a very small exponential function, still increases at a much slower rate. Even with a value of Nas small as 1000, you can see that Shor’s algorithm would run in a much shorter time than the regular computational algorithm.

The natural question then becomes, are there any algorithms that are not perceptible to these types of schemes? Well, in theory, yes. One method exists, aptly called the One Time Pad, though it is not very practical. The OTP is information-theoretically secure, which mean that an adversaries’ computational abilities are inapplicable when it comes to finding the message. However, OTP uses a pre-shared key in order to decrypt and encrypt the information. So the information that is being sent is secure, but the problem is how to efficiently share the key between the sender and the recipient. Using OTP’s would require a meeting with the other side directly, or alternatively using a trusted courier, but if this was available you could just send the message using this channel, making the encryption fairly irrelevant.

Epilogue

So, are we destined to live our lives completely in the public eye? Will Big Brother come to pass? Probably not. There are multiple alternatives that while not imperceptible to these types of attacks, are certainly a lot stronger (AES is one such example). There is also the problem that quantum computers are quite a way off being able to reliably implement Shor’s algorithm. Not only are there limits to how powerful we can currently make quantum computers, but there are also multiple quantum phenomena that impact calculations and make the results unreliable (like quantum noise and other quantum-decoherence phenomena). Another thing to consider is that with the breaking of old algorithms comes the creation of new ones. There is still a lot of unknowns about quantum computing, and it would not be amiss to think that new ideas could be discovered that would make things like the RSA algorithm obsolete.

For now, at least, all your information is safe. You can go ahead and send a text message, knowing that only yourself and the recipient will be able to read the message. All thanks to Diffie and Hellman who started the journey, and Rivest, Shamir, and Adleman, who were able to see it through.