This interesting math trick arises from an interesting empirical observation and the Fibonacci sequence. First, we should define the relationship between miles(mi) and kilometers(km):

1 mi = 1.60934 km and 1 km = 0.621371 mi

Now, if this number looks familiar, it is because these numbers are extremely close to the golden ratio.

By noticing the golden ratio is close to the conversion factors of miles and kilometers, we can rewrite the relationship between miles and kilometers as an approximation:

(If you want to skip the proof, then skip this section).

Connecting Fibonacci to the Golden Ratio

As promised by the title, I will be showing how the Fibonacci sequence converts miles to kilometers, but first, we need to establish a connection between the Fibonacci sequence(F(n)) and the Golden Ratio(φ). To do this we are going to use Binet’s formula:

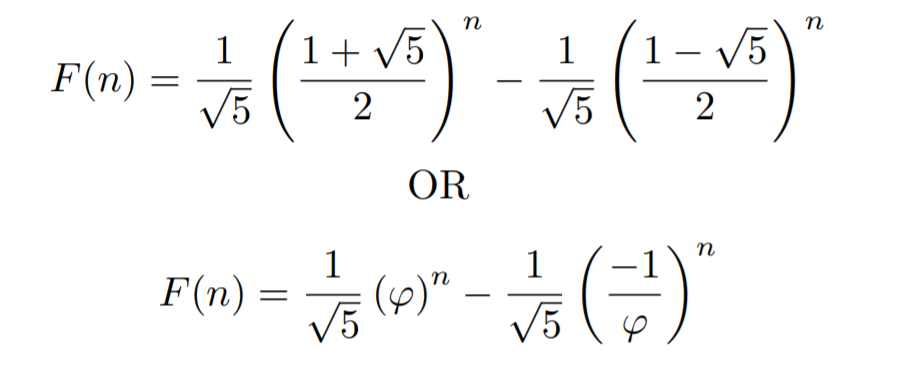
(If you want to see a proof for how Binet’s formula is derived, here is a link to a previous article I have written-Link)

And it is easy to notice that the Golden Ratio is sitting inside Binet’s formula. Now, we need some kind of formula to explicitly draw out the golden ratio, in terms of the Fibonacci sequence. To isolate φ, let’s try taking the ratio of subsequent terms:

At this point, I am going to make an argument, to make computing this monstrous limit easier. Since 1/φ < 1, as n keeps on increasing, they approach 0. Hence, we can get rid of 1/φ part of the numerator and denominator and cancel out the constants. This leaves us with:

This gives us the approximation:

which looks awfully close to-

The Final Stretch

Just a quick refresher, the first few numbers of the Fibonacci sequence are 0,1,1, 2, 3, 5, 8, 13, 21, 34, 55,…

Now, what the approximation above is telling us is that multiplying a Fibonacci number by φ, is roughly the same thing as finding the next Fibonacci numbers.

Using this argument, if we were told to convert 5 miles to kilometers, we would find the next Fibonacci number, which is 8, so our approximation is that 5 miles = 8 kilometers. In reality, 5 miles is 8.04672 km.

Now, what if we wanted to convert 10 miles to kilometers. 10 isn’t a Fibonacci number, so we have to rewrite 10 as the sum of Fibonacci numbers (8+2). Then, we get (8+2) mi = (13+3) km = 16km. If we used the actual conversion factor, we get 10 mi = 16.0934 km.

What if we wanted to convert from kilometers to miles? If multiplying by phi is associated with finding the next Fibonacci number, then dividing by phi can be associated with finding the previous Fibonacci number.

So, an example would be converting 42 km to mi. First, we split 42 into a sum of Fibonacci numbers, (34+8) km = (21 +5) mi = 26 mi. If I used the actual conversion factor, you get 42 km = 26.0976 mi.

Concluding Remarks

By no metric, is this considered serious math. It is just an interesting trick that came from closer observation. However, I would like to point out that this is an example of how beauty emerges from the randomness of the universe. No one thought of the golden ratio or the Fibonacci Sequence when coming up with miles and kilometers, yet this connection exists.

If you made it this far, thank you for reading. I plan to explore more topics surrounding the Fibonacci sequence in the near future. For now, goodbye.

Update

I have written another article on the Fibonacci sequence, check it out if you want:

Why does 1/89 represent the Fibonacci sequence?