Being German, I have been asked about the famous German Autobahn more than once. It also means that I have a lot of discussions about (non-existing) speed limits on (some) German roads and I have spent countless hours discussing whether speed limits (on highways) are a good thing or not.

Even though I mainly approve of speed limits, this story is not going to be about them.

It is not going to be about whether or not driving as fast as you want should be allowed or not. It is not going to be about whether it is safe to drive fast or whether driving slower leads to fewer accidents compared to driving fast.

This story is about optimizing traffic flow and trying to squeeze in as many cars onto the ever-growing busy roads as possible.

Because a common assumption is that, by going faster, you will also be able to fit more cars onto the streets and thus increase traffic flow.

The assumption is that traffic on the streets is a lot like traffic on the railroad. And there, if you have faster trains, more wagons may travel from A to B in a given amount of time.

But with cars, it is not that straight forward. Let’s explore why.

The Simple Solution: Maximizing Traffic Flow

The velocity of a car (or any object) is given by distance traveled divided by the time it took to travel that distance.

We can also use this formula to calculate the time between any two cars on the highway. Here, we do not only need to factor in the distance d₂ traveled by the car, but we also need to consider the length d₁ of the car.

Thus d is given by the sum of d₁ and d₂ and we can use this to calculate the time between any two cars.

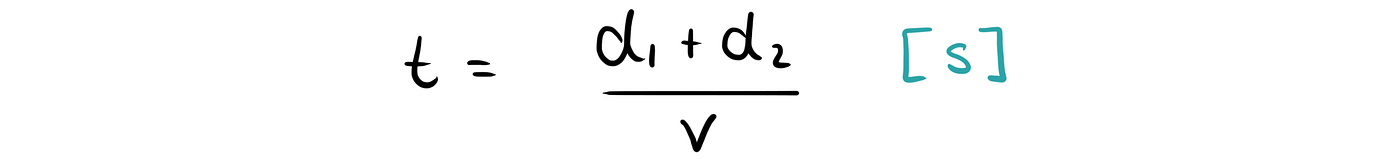
We can now use this to calculate the traffic flow F(v) which is measured in cars per second and depends on the speed of the cars.

In an hour there are 60 ⋅ 60 = 3600 seconds.

Thus, the traffic flow F(v) is given by

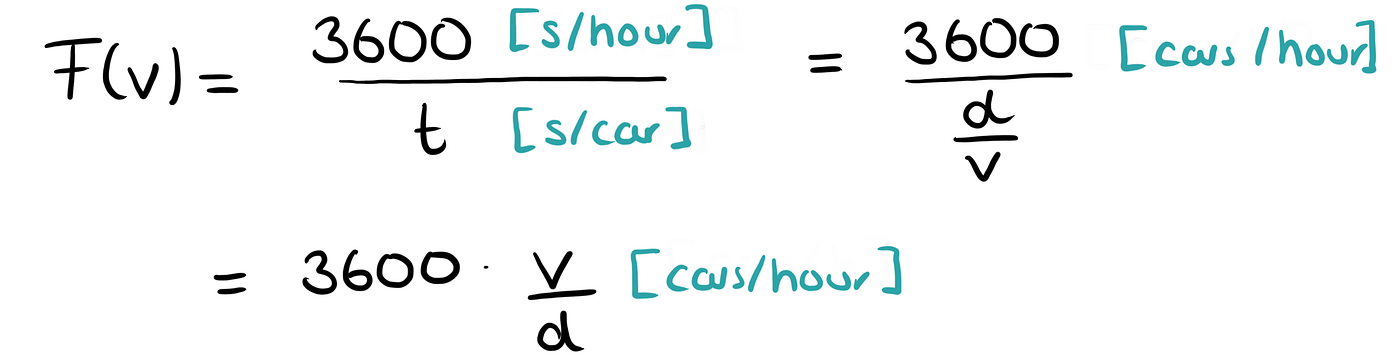
Taking into account that the time between two cars t depends on both the length of the car d₁ and the distance d₂ traveled by the car, we have a traffic flow F(v) of

The length of the car d₁ is fixed, but we can influence the distance between cars and the speed at which they’re traveling. Let’s plot the traffic flow F(v) for various parameters d.

So the solution to maximize traffic flow seems quite simple.

To increase traffic flow, lower your distance or increase your velocity.

It seems simple, doesn’t it? Well, I have to disappoint you, because is it not as simple as it seems. This argument only contains part of the truth. Because the faster you go, the bigger the distance to the car in front of you will be (or should be). If you’re going at 200 miles per hour, there is no way you would be able to keep a small distance without increasing your likelihood to crash into that car in front of you.

That’s why this simple formula only works for railroads, where you have one unit opposed to many single cars that speed up and brake individually.

Factoring in Braking Distance

This is why we need to make this setting a little bit more realistic. Let’s factor in the distance it takes to brake. For this, we need to consider two things:

• the time it takes for someone to realize that they need to brake
• the actual time it takes to come to a full stop after starting to brake

Usually, one assumes that it takes roughly one second of reaction time to realize that braking is necessary. Since the distance d₃ traveled in that second is given by velocity times time, it is given by

This means, that by the time someone realizes that they need to brake, they have already traveled v meters.

Now we still need to determine how much time it takes to come to a full stop once we started hitting the brakes.

To come to a full stop, we can now use the formula for acceleration

Taking in a “deacceleration” of roughly 10 m/s² (so 10 m/s of deacceleration per second), which seems realistic, the distance d₄ traveled during the braking process is given by

Thus, the total distance d₅ that the car travels during a full braking process is given by

Therefore, the traffic flow can be calculated by

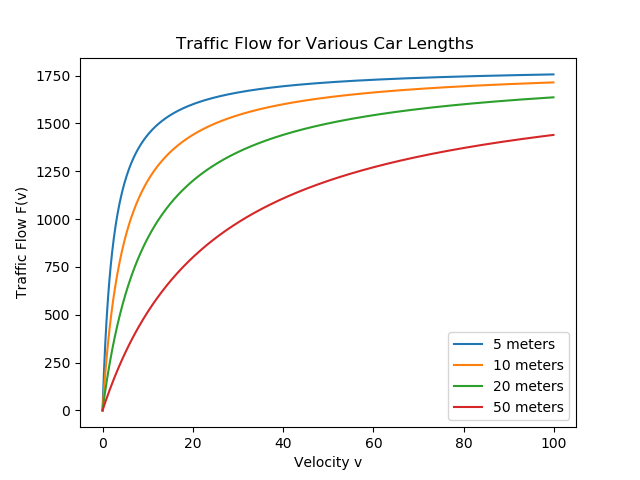
Again, let’s plot this first using various car lengths and a=10m/s².

From the curve, we can tell that there is an obvious maximum somewhere. We can calculate this mathematically by determining the derivative, setting it to 0 and double-checking with the second derivative whether this is actually a maximum.

Let’s start by calculating the derivative.

Let’s set it to 0.

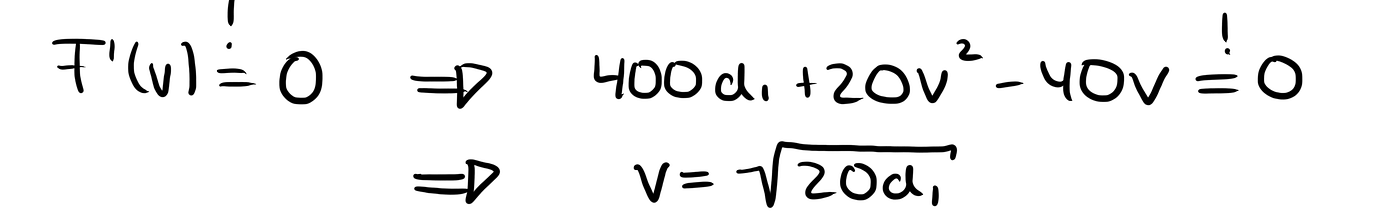
Doing this leads to an optimal speed of the square root of 20d₁.

(In fact, we’d have to double-check whether this is a maximum by using the second derivative and checking the boundaries, but as it is obvious from the graph, we will skip this part.)

So if the average length of a car is only 5 meters, the optimal speed (to maximize traffic flow in this model) is 10 m/s or 36 km/h or roughly 22 mph! For larger cars or trucks which may have an average length of 20 meters, this leads to an optimal speed of 20 m/s or 72 km/h or roughly 44 mph!

Sounds already better, doesn’t it? But unfortunately, this is not very realistic either. Because if you start keeping very large distances to the person in front of you, somebody else will surely try to squeeze in.

2 Second Rule: More Realistic Braking Distances

That’s why, again, we need to be more realistic here. And people on highways do not keep that much of a distance. And in fact, it’s okay to keep less. Because if the person in front of you starts to brake, you can start braking too. So the general rule is not to keep a distance of v+v²/20 meters, but to stay “2 seconds behind”. And thus we only need to keep a distance of

to be safe. This then leads to a traffic flow of

which looks a lot more simple than the formula that we saw in the previous section.

Let’s also plot this for various car lengths.

From the graphs, we can tell that this time, there is no maximum, but rather, the graphs seem to flatten out. We can show this mathematically by calculating the derivative.

As we can see, it only takes positive values, thus the traffic flow is increasing with velocity.

But it will not increase to infinity but it will flatten out eventually. In fact, if we look at the limit for v towards infinity, we can see that the traffic flow maxes out at 1800 cars per hour.

And the smaller the cars, the faster we get closer to this number.

So no matter how fast the cars go, there will never be able to be more than 1800 cars on the road if they’re maintaining an adequate distance.

And thus, speeding may not be the solution to maximizing traffic flow.

Some Final Words and Considerations

It’s impossible or at least very tough to formalize everything that happens on highways. So when people scientifically research traffic flow, they usually do it by simulation instead of squeezing it into formulas the way I did.

And, by simulating traffic, one gets a lot more interesting insights. For example, simulation of traffic shows that the worst that can happen is people speeding and braking suddenly, which then leads to traffic jams and decreased traffic flow.

So even though speeding may be great if the highway is empty and you wanna get from A to B very fast, it is not always the solution for everything. Especially not if space is limited and lots of people want to travel. Because it will not lead to increased traffic flow and it will just lead to more traffic jams.

So, therefore — to increase traffic flow, speeding is not the answer.

Sorry fellow Germans and friends of the Autobahn.

A little note: Please drive responsibly. Don’t kill yourself or other people out there on the roads. Don’t speed where it’s not necessary or plain dangerous. I’m not advocating speeding here. I think speed limits are there for a reason. And when there are none, it usually means that it is safe to drive fast.

Also in Germany, we have speed limits in most areas, but there are a few places where the streets are wide, the traffic not too busy and where you are allowed to go as fast as you like or can.