How Eratosthenes Calculated the Circumference of The Earth

About 200 years BC in ancient Greece, scientists in those days were convinced that the spherical shape of the Earth, and not a flat disk, was correct.

Pythagoras considered a circle perfection to be upon any other, and as such, fits best to describe the excellence of the world.

Aristotle argued in his philosophical considerations about the theory of five elements. These describe all physical states, which, considered separately, must strive for the most perfection, that is to a circle.

After all, when during a solar eclipse, the spherical moon casts the shadow on the Earth, the same must happen when they swap in places during a lunar eclipse, causing the moon to be in the shadow of the Earth. Observation of the phenomenon reveals the shadow gradually covering the moon has a spherical shape. So if the Earth is the source of this spherical shadow, then it must be spherical itself. Pretty reasonable and accurate reasoning, right?

Right.

So Eratosthenes was convinced of many things back then.

But how big are you, my Earth? How?

It is obvious that one could not just go around the Earth, counting steps, and, when finished, multiplying it by the average distance taken in one, resulting in the circumference of the Earth.

Thus what was the way?

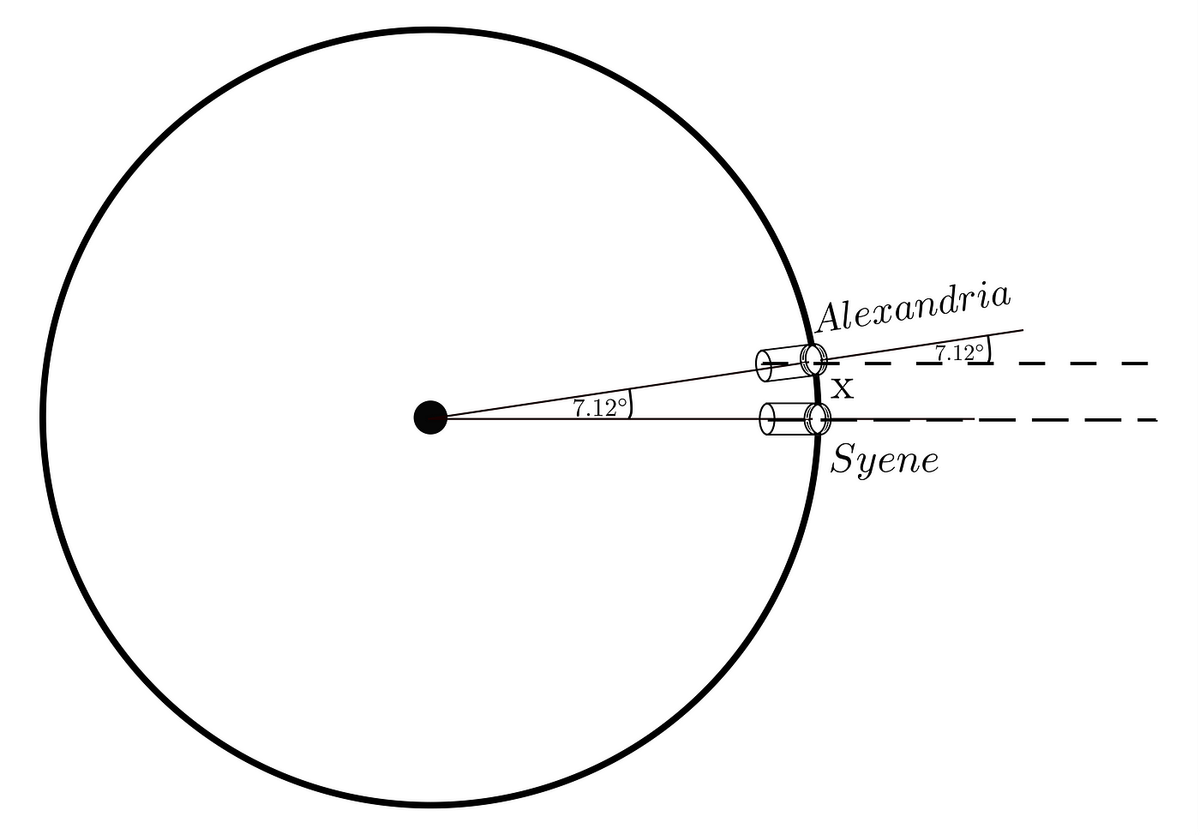
Observing the summer solstice in Alexandria, he was watching the illuminance of the pit of a well at noon, noticing it was not quite full. There was a black spot on the bottom not illuminated by the sun.

Thus, having sun exactly overhead and by believing that its rays are parallel to each other, it was clear they cannot be perpendicular to the surface, but they have to be inclined at some angle; therefore, to find out at what, he stuck an ordinary stick into a ground and measured the angle between it and its shadow.

The result was 7.12°.

Later he has heard that each year during the summer solstice, the sun’s rays falling on the bottom of a well in Syene illuminate its entire pit. He was intrigued by this fact because it would mean, that unlike the well in Alexandria, the sun’s rays fall perpendicular here. Only sphericity of the Earth could explain that the sun’s rays running parallel fall on the Earth’s surface at different angles during the same time. And if so, the Earth must be rounded. So if it is, as he has heard, it would be next evidence of the Earth’s sphericity.

Consequently, he decided to check this fact, going there on the day of the summer solstice to observe this phenomenon. It turned out that indeed, there was simply no shadow in Syene. It profs the spherical shape of the Earth.

But how to come up from this fact for calculating the circumference of the Earth?

Eratosthenes thought the following way. Well, the difference in angle between these two cities is equal to 7.12°, which is 50.56 times less than a full circle. Thus if one measures the distance from Alexandria to Syene and multiply it by this amount, then what got has to be the circumference of the Earth!

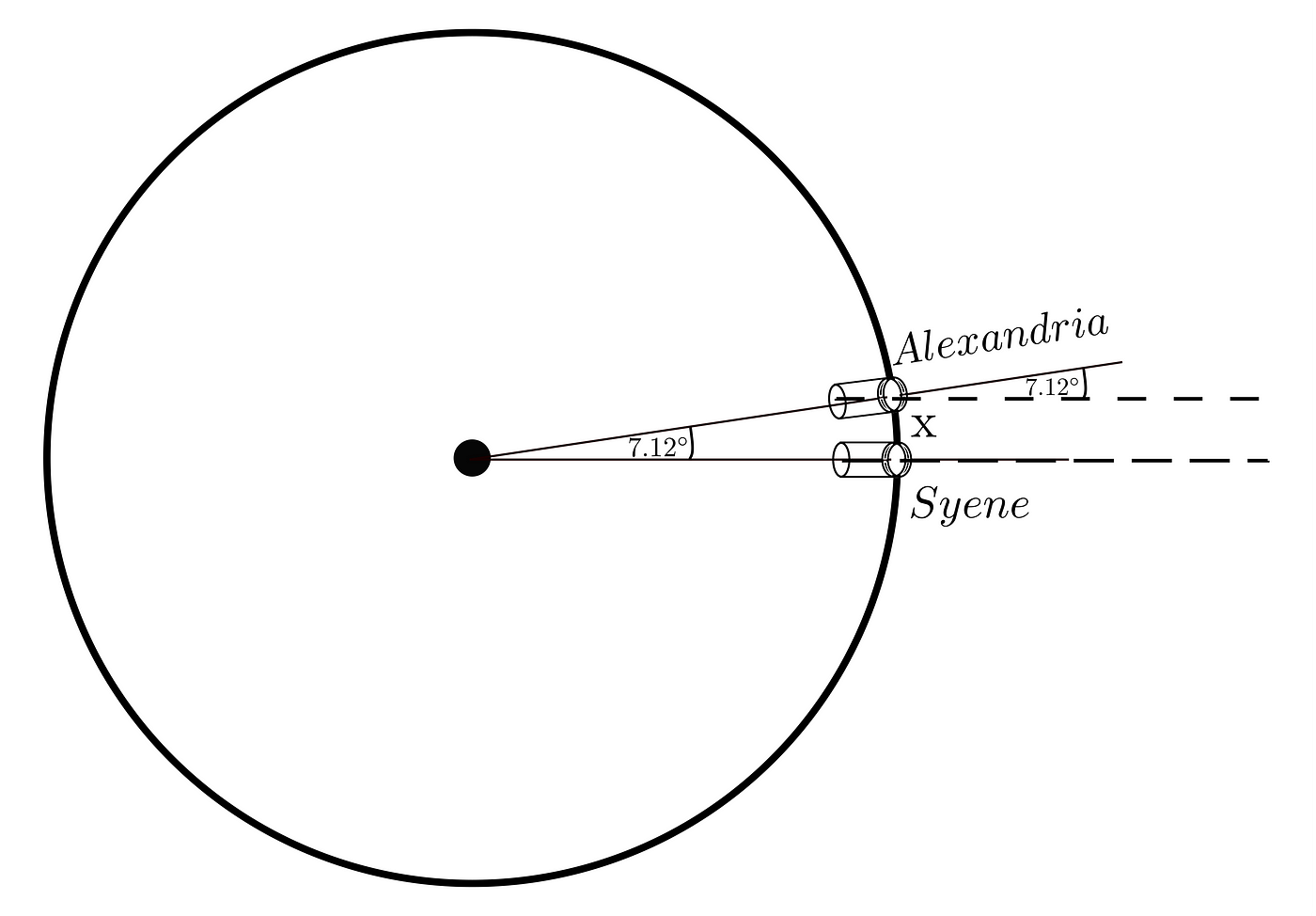
However, the way he determined the distance x between these cities is not entirely clear. Some say he used caravans’ knowledge and the fact that camels travel at a more or less constant speed. Others say that he measured this distance himself or hire someone to do it for him. What I believe in is having the soul of the scientist had to force him to check all data used in calculation somehow that has not come from a reliable source.

Anyway, he got a distance of 5000 stadia, where one is equal to 600 Greek feet. And here we have a little confusion about the exact result because it was not the same everywhere in Greece, let’s take the one he probably used, that is 185 m. That is:

thus we or actually he got a distance:

where the real value is 40075 km.

And that is how he did it and as seen he was not that much off. Especially when considering his thoughts of our planet as exactly spherical, what we know is not entirely true.