So far, Earth and Moon’s sizes are not puzzles anymore for us. They are quite well known since Erathosteneles derived the first and Aristarchus the second. But it is not like no mysteries out there left. There are dozens still. Where the next, natural step leads to derive the distance between the two of them.

Aristarchus and Hipparchus did not live within one time. 40-years apart was between them. Aristarchus died 230 BC, while Hipparchus was born in 190 BC. So, he was a descendant of Aristarchus’ and earlier Greeks knowledge. That is why the ancestor’s approach should go first.

Aristarchus’ way

Aristarchus used the triangles’ similarities to measure the distance. The idea came upon him during a solar eclipse. He understood the shadow then has a cone shape, while the Moon and the Sun have circular disks. So, he could do the same with the Moon and another object. By scaling it about his eyes until not blocking the whole Moon, he created his own cone.

After a while, the object suited. But, of what kind it was? Something with a circular disk. Like a coin. And indeed, some coin is what he used. He took one and found the position by moving it up and down. Now, he already knew all.

Of course, their angular sizes were equal because the coin covered the Moon. It means that their observer’s triangles had the same angles. Thus, they were similar.

Similar triangles bare the proportion property. If corresponding angles are congruent, then also their sides are in proportion to each other.

Aristarchus estimated the ratio of the coin’s distance to its diameter as 108.

Based on that, he concluded the ratio of the Moon’s distance to its diameter to be also as such.

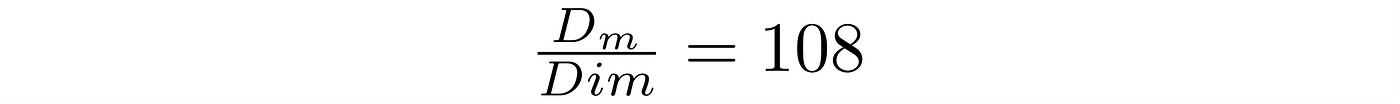
And, since only the distance to the Moon was unknown, the equation:

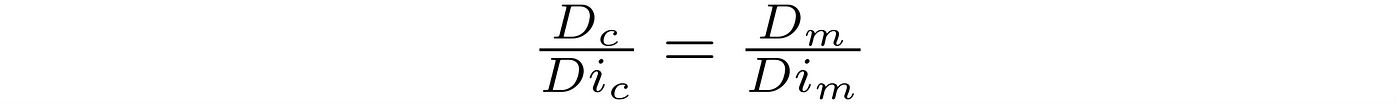
could be solved because Aristarchus derived the Moon’s diameter to be as 1/3.5 of the Earth’s one.

After a moment of calculation:

And this result was pretty accurate indeed.

But, what exactly?

To show it, we need to make an extension of Erathosteneles’ circumference calculation. From there, the Earth’s radius has to be calculated, but it should be a piece of cake. That is:

Now, we need to double it to get the diameter, thus:

And substituting it to the equation:

Hipparchus’ way

He made a reasonable assumption from a solar eclipse observation in Syene and Alexandria. The cities from which Erathosteneles calculated the Earth’s circumference. And that is not the end of the similarities. Because he also used the distance between them, which one he knew since Erathosteneles measured it earlier. So, what was the way of Hipparchus?

The major part was to measure how much of the Sun was seeable in Alexandria when the Moon was entirely over the Sun in Syene. It appeared that the partial eclipse was one-fifth of the Sun’s disc. Moreover, the angular size of the Full Sun is a one-half degree, so one-fifth of this equals one-tenth of a degree. It was the difference in the apparent angular sizes of the observation between the cities. Adding within there a pinch of geometry, made him derived an independent method than Aristarchus’ one was.

By applying the small-angle approximation to the given observer’s triangle (equivalence of tangent function), he got:

57.3° is in the denominator because it is how many degrees 1 radian has. Computing the right side:

And now by rearranging the equation to get the distance:

What gives: