How Aristarchus Found the Size of the Moon

Last time we followed Eristarchus’ steps of measuring the circumference of the Earth. Today, we will push forward in our investigation of how big the universe is. Because, again, we are hungry for knowledge.

We know what the size of the Earth is. So let us go up there and see the one of the closest celestial body. By leaving the ground, raising our heads, and merely looking at the sky, we will be struggling to quench the thirst... keeping on track of Aristarchus. The man who found a way of measuring the size of the Moon, and who first claimed the heliocentric over the geocentric system — where all orbits are perfectly circular.

He believed that gathering enough information on a qualitative observation makes it also descriptive quantitatively. It means that by sketching a lunar eclipse event, while being on Earth, someone could find the quantitative description as well.

So. How big are you, my precious Moon?

Well, everybody knows that the sun is much more distant and much bigger than the Moon, but it is not like we have that knowledge with birth. Yet, the observation of a solar eclipse reveals that, for its duration, the Moon covers the sun, and not different. From this fact, it is evident that it is, indeed, the closest celestial body.

Observation of this phenomenon shows additionally the sun’s and the moon’s disks fit as one to one: they have almost the same angular sizes. This and the fact that the Sun hides behind the Moon speaks for itself — the Sun has to be bigger than the Moon.

Aristarchus has known that during a lunar eclipse (when the Sun, Earth, and Moon, are set in a straight line in that order) the Moon “disappears” somewhere for 2 hours. He reasoned it moves through the earth’s shadow then. Since one of his assumptions touched the source of the moon’s light: he assumed, what causes the moon’s visibility is a reflection of the sun’s rays from its own surface. Hence, if something were to block sunlight falling on the Moon, it would make it invisible. And during a lunar eclipse, this something has to be the Earth because simply there is nothing else around.

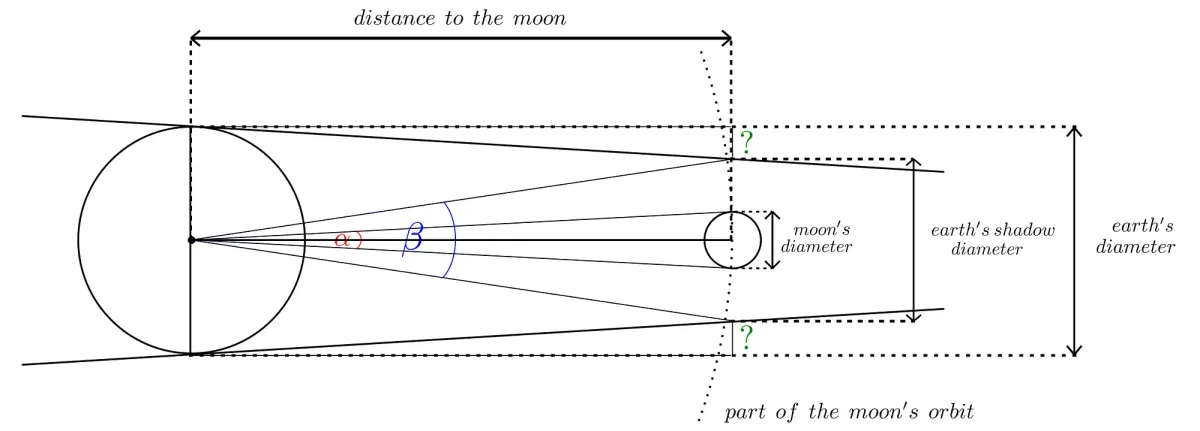
Let us focus on details of his observation of a lunar eclipse. He has started by forming the ratio of the angular sizes of the earth’s shadow diameter to the one of the Moon. The first was measured by comparing the positions of the Moon just before tapping into the shadow to the one just after leaving it. The second (he thought the Moon orbit around the Earth to be perfectly circular) could be measured during the Full Moon at any time. But what for he needed that? Both of them are at the same distance from the Earth, so the ratio of their angular sizes has to be equal to the ratio of their physical sizes. It could not be different than that. It was about 2.5.

The earth’s diameter was only known quantity to Aristarchus: it was given earlier by Eratosthenes. The above picture shows that two lacking segments plus the earth’s shadow diameter would equal to it. So, while they are at the same distance from the Earth as the shadow and the Moon, computing their lengths in relation to the moon’s diameter will give the whole length equal to the size of the earth's diameter. It would be 2.5 (from the earlier ratio) + 2? (from the picture). And this had to be calculated.

But the equation:

has two unknowns. So we need an additional one that will have the same unknowns. And, because the angular sizes of the Moon and the Sun are equal, it is quite reasonable to try finding this equation on the opposite side of the earth’s orbit. So let us add the Sun to the picture.

A moment of thought and a sharp eye to detect a straight line, and a triangle (upper or lower — both are identical), which angles sums to 180°, and which have one common angle.

Notice the angular size of the sun is labeled as α. We told earlier it is identical to the angular size of the Moon, so we could write this in the same way. Thus:

By substituting ϵ of the second equation, that is:

to the first, we get:

Now, by approximating a few things, the relationship of a triangle sides to its angles could be used to calculate all of them. And, since we are in a cosmic domain, we could do it. The earth’s shadow diameter is approximately the arc length of β at the distance to the Moon. The slant heights of the shadow’s cone from the Earth are approximately the distance to the Moon, and these from the Sun to the Earth are approximately the distance to the Sun.

Applied the tangent formula gives:

Substituting them into our equation results with:

where the last one is negligibly small. Aristarchus thought of the Sun distance as 20 times larger than the Moon. Therefore, he did not take this factor into account. The equation then looks like this:

And after a while:

Voilà. Our principal question was how much we should add to the earth’s shadow diameter to get the earth’s diameter itself. And the answer is that we should add the diameter of the Moon. So, each of these sectors we attempt to calculate has the length of the moon’s radius. Thus we get:

I would say since the real value in the denominator should be 3.6699; it was a pretty good guess from Aristarchus.