How Aristarchus Estimated the Distance to the Sun

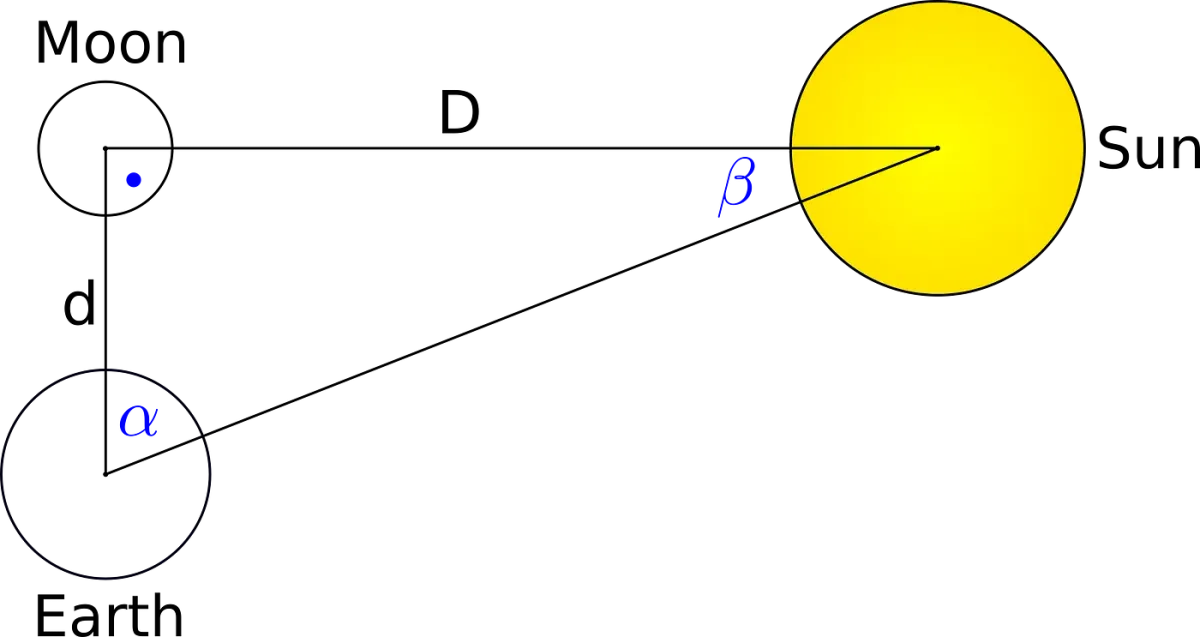
Here we come in our journey through the past across the first substantial error in science that I want to talk about. Aristarchus measured the distance to the Sun to be 20 times more than that from the Earth to the Moon, which was off by the factor of 20. To clarify, however, it did not come out from wrong reasoning but merely because of technology gaps. And so scenarios had and will repeat all over again. What do I mean by that?

I have no doubt that if Aristotle were alive in the 17th century, he would figure out the gravity the same as Newton did. Also, if Isaac Newton were alive around the turn of the 20th century or sneaked somehow to the future and saw results of experiments congruous to Michelson-Morisson’s one, he would adjust his law of motion to relativity effects. Do not have any illusion, it applies to our times as well. We surely give credit to something that in the future will be considered as not entirely true (do not confuse it with wrong.)

Science and technology are so strongly correlated that they can exist only together. They are “yin-yanged.” Once one goes ahead a little, it cannot go any further until not caught up by the second. They attract each other with a mystical force, and it pays off.

That is the reason behind Aristarchus’ overall mistake. He had sailed on unknown waters. It means, he made astronomy to lead at one step while many centuries have gone before technology made up this loss. But, as I said, which I believe you agree with, they come as a pair, neither could be ahead. So, the machinery stopped until the telescope invention in the early 17th century.

Keeping that in mind, we can talk now about Aristarchus’ way of measuring that distance.

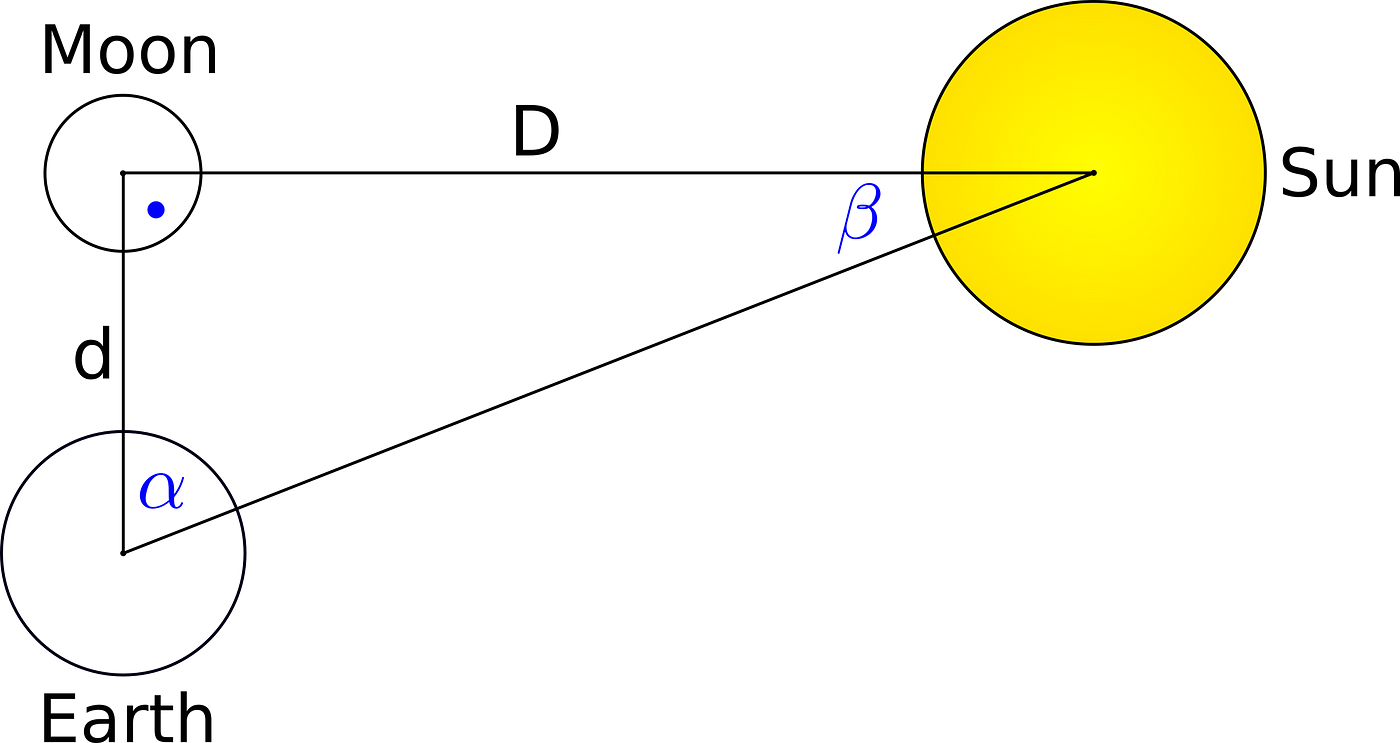
As shown in the picture, we have some configuration of the Earth, Moon, and Sun. The only question is, what is the condition to have the right angle in the above triangle at the Moon position. The key to the answer is its shadow distribution. Stating differently, what part of the Moon must be seeable from the Earth, and what not? It has to be a Half Moon, what, after giving it a little thought, does not surprise. So, Aristarchus had to wait for his opportunity, and when it came, he measured the α. It was about 87°.

From the property of angles in triangles:

Now, using the tangent function (Aristarchus used the observer’s triangle property; however, it is equivalent to the tangent. So, I prefer to write it down in a way that is commonly known and will not confuse anybody.)

and rearranging terms to get the distance, D:

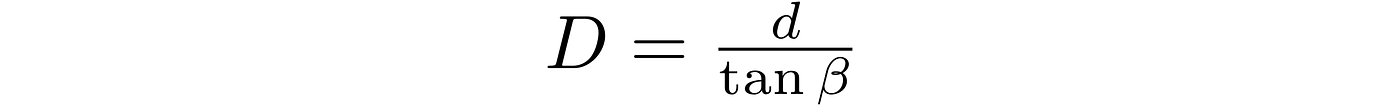
finally, by substituting β and calculating the denominator:

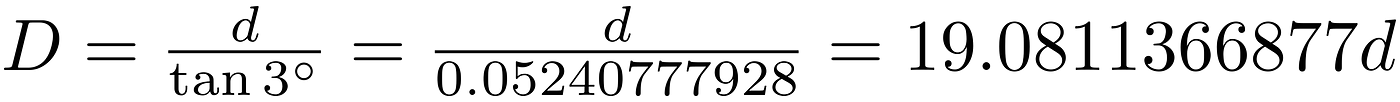
So, yeah, it was quite off.

When the telescope became a thing, Godefroy Wendelin, a Flemish astronomer, made a significant correction in this calculation. With help from a telescope, he was able to get a much more precise focus on the Sun. And, he corrected the β’s value from 3° to 0.3°, which set the distance to the Sun as 190 times the Earth-Moon’s one.

Still, it was more than twice too low, but it could not be denied that it was a step forward.

The more accurate measurement, which gave almost the right value, was made according to Edmond Halley’s idea, in 1739. It was based on observation of Venus’ transit as seen from different points on the Earth. But, it deserves a separate story to be told in.