Henri’s Adventures in Phase Space

What is a dynamical system and why would I care?

A dynamical system is used to describe how a system changes over time. This system can be used to describe a whole hoi polloi of phenomena: from a ticking grandfather clock to the movement of galaxies. From electrical circuits to the spread of HIV. Think of anything that changes over time and chances are you can write a dynamical system to describe it.

The objective of this article is to present an intuitive explanation to some core concepts in the study of dynamical systems.

Meet Henri

I like to think about a dynamical system as a man standing in a field with a rule book. Let us call him Henri, after Henri Poincaré — one of the founding father of dynamical systems. At each point in the field, Henri looks it up in the book which will give him a direction and a speed. He then walks in that direction at the given speed for a fixed amount of time. Henri now finds himself at a new point on the field and repeats the process. Tracing his path, gives us a jagged line across the field.

Now we reduce the amount of time he spends walking in a fixed direction. This will file down the edges of Henri’s path over the field and we will reach a smooth path. This is called the trajectory. The point Henri starts at is called the initial condition.

Now the field Henri is standing in doesn’t need to be flat. It can have ditches and hills and holes. It doesn’t even need to be a field — it can be a path (i.e. on which Henri can only move left or right) or it can be some ball hanging in space (granted, Henri would have to have some sort of suction device to stay on) as long as our field is sufficiently smooth without any cliffs or rough edges and doesn’t end abruptly. We could also allow Henri to fly, allowing him to go in all directions in the sky. The field or space that Henri lives in is called the phase space.

The rule book along with the space that Henri lives in is called a dynamical system.

Henri takes a walk

Let’s restrict Henri to living on a field that extends forever in every direction.

The big question of any dynamical system is

Given where Henri starts, where will he be in the future?

This can sometimes be trivial: if the instructions for each point is to move due east at 1 m/s then in 5 seconds he will be 5m east of where he started (we have to make a choice of what defines a meter or where east is in Henri’s world but let us assume that we can make such a choice). There is a small collection of rule books for which we can give a precise answer like this to our question but more often than not we don’t know exactly where Henri will be but we can figure out some of his behaviour or where he will end up.

Let’s start of simple. Is Henri moving? If he is not moving then that must mean that the instruction for where he is standing is telling him to not move anywhere. Consequently he will stay fixed at that point forever. Unsurprisingly this point in the field is called a fixed point.

Now let’s consider the case where Henri is moving. There are two possible behaviours of Henri’s trajectory.

• Henri stays inside some fenced area
• Given enough time, Henri will escape to infinity

The later case is not interesting and so I won’t discuss it further. The former case however is particularly fruitful.

We suppose Henri is stuck inside some fenced area and unable to escape. Henri can either come to a stop or he will be forced to cross his own path. Now if he stops then he must have hit a fixed point and so will stay there forever. If he crosses his path then because he has to follow the same rule at that point then he will be forced to repeat that section of his path and so will be stuck in that periodic loop forever. This is called a periodic orbit.

If you think hard enough, these are the only two options since Henri is stuck in a finite area.

To recap what we have discovered:

If Henri is stuck in a fenced region, then he will either end up at a fixed point or going around in a loop forever.

This in fact is what is called the Poincaré-Bendixson Theorem which states

Let ẋ = f(x), f ∈ C¹ with associated flow ɸ. If there exists a forward-invariant compact set K diffeomorphic to a closed subset of ℝ ² then for all x ∈ K, ω(x) is one of the following:

1. A periodic orbit

2. A compact connected set consisting of a non-empty set E of fixed points and some (possibly none) heteroclinic and homoclinic orbits connecting points in E.

Now I don’t know about you but I much prefer the former explanation. The first version is much more appealing, and Henri allows us to understand the intuition behind this.

Henri takes a tumble

Now that we understand the possible local behaviours of Henri on a field, let’s switch things up. We insist our field has hills and valleys and be bumpy. We will require that our field has no cliffs and it be nice and smooth.

Henri now will move by following the steepest descent; at each point the rule book tells you to go in the most downward direction possible and then the speed is given by how steeply you are going down.

Since Henri is walking around on a field, he can either escape to infinity or stay inside some fenced region where we can apply the Poincaré-Bendixson Theorem and decide that Henri will end up either stuck in a fixed point or in a periodic orbit. Now if you think hard enough, Henri can’t fall into a periodic orbit since to get round to where he once was he would have to go back uphill which is not allowed by his downward trajectory. So Henri will always end up at a fixed point or off in the distance going to infinity.

Let us investigate what these fixed points can look like.

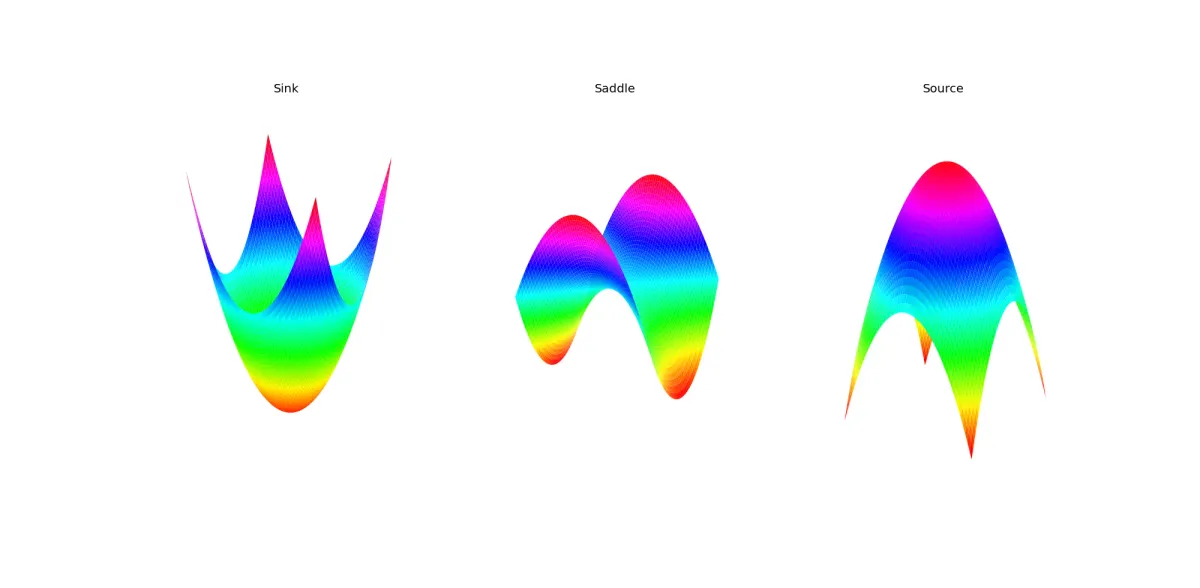
The most obvious one would look like the bottom of a bowl or a pit, Henri will walk down towards it and will stay there. This is called a sink, because if Henri starts near it, he will sink into it — this property is called being (Lyapunov) stable.

The next kind of fixed point we can have is at the top of a hill. If Henri starts there, there is no downward direction and so he will stay there forever, this point is called a source. Unlike a sink, if he starts near it, he will walk away from it. Similarly to before, this property is called being (Lyapunov) unstable.

The third kind of fixed point is a col or a saddle since it looks roughly like a horse’s saddle: in one direction the field curves upwards and in the other it curves downwards.

These are the only types of (non-degenerate) fixed points both in the plane and in higher dimensions. Degenerate fixed points are a lot more complicated, but we will explore one called a center later on.

Henri destabilises

We consider again a bumpy field with the steepest descent rule. Let’s put Henri near a sink. Recall that this fixed point is stable, so Henri will tend towards it. Now imagine we push up the pit slowly, it will remain a sink but will be shallower until it goes through a perfectly flat field (which is said to be a center) and then turn into a peak which is unstable.

By smoothly varying the field, our fixed point has gone from being stable to unstable through a sudden change. This change is called a local bifurcation and occurs when sections of phase space change stability. I say sections because it can be fixed points, periodic orbits or more complicated stuff.

Henri reaches cruising altitude

We now change Henri’s rule book. Instead of heading downhill, we make him move along contour lines. That means he moves along whilst maintaining his altitude and keeping the downwards direction to his right (this is somewhat arbitrary since we can reverse his direction and make him keep it on the left and one of the key properties of these kinds of systems is that it is reversible), his speed will be given by how steep the slope is. So Henri will be walking along a flat path. This is called a Hamiltonian system, and is the basis of most of modern mechanics.

With this rule book, we can recover exactly the same fixed points. But now we get a new behaviour that we didn’t get in the steepest descent rule book: Henri can be stuck in a periodic orbit. If he starts off in a bowl, slightly off of the bottom, he will keep the bottom on his right and continuously spin around the bottom fixed point. Since he does not change altitude, once he has gone around the bottom once, he will be back to where he started and is doomed to repeat that forever: he is in a periodic orbit.

No matter where we start him off in the bowl, he will be trapped in a periodic orbit. The bottom of the bowl exhibits behaviour similar to that of a flat field — If Henri starts near the bottom, he will stay near but will not get any nearer. The bottom is a center and we say that the centre is foliated by periodic orbits.

Henri collapses

We can create more interesting bifurcations in a Hamiltonian system. If we consider two bowls near each other. There will be two centers and one saddle between them. Depending on where we start Henri off, he will either be on one of the three fixed points, or will be on a periodic orbit around one or both centers. Now we move the bowls closer and closer together until they collapse into one. Now we no longer have our saddle point and we only have one possible periodic orbit going around the super bowl. The two periodic orbits collided into one. This is another example of a bifurcation but in this case it is a global bifurcation since it involves the destruction (or creation) of so-called invariant sets.

Concluding remarks

This was a gentle introduction to the qualitative study autonomous differential equations in the plane and some bifurcation theory. Whenever I have to deal with new or complicated concepts, I like to construct the simplest model in my head to try and get an intuitive understanding of maths and in my opinion is far more important than staring at pages and pages of dense notation.

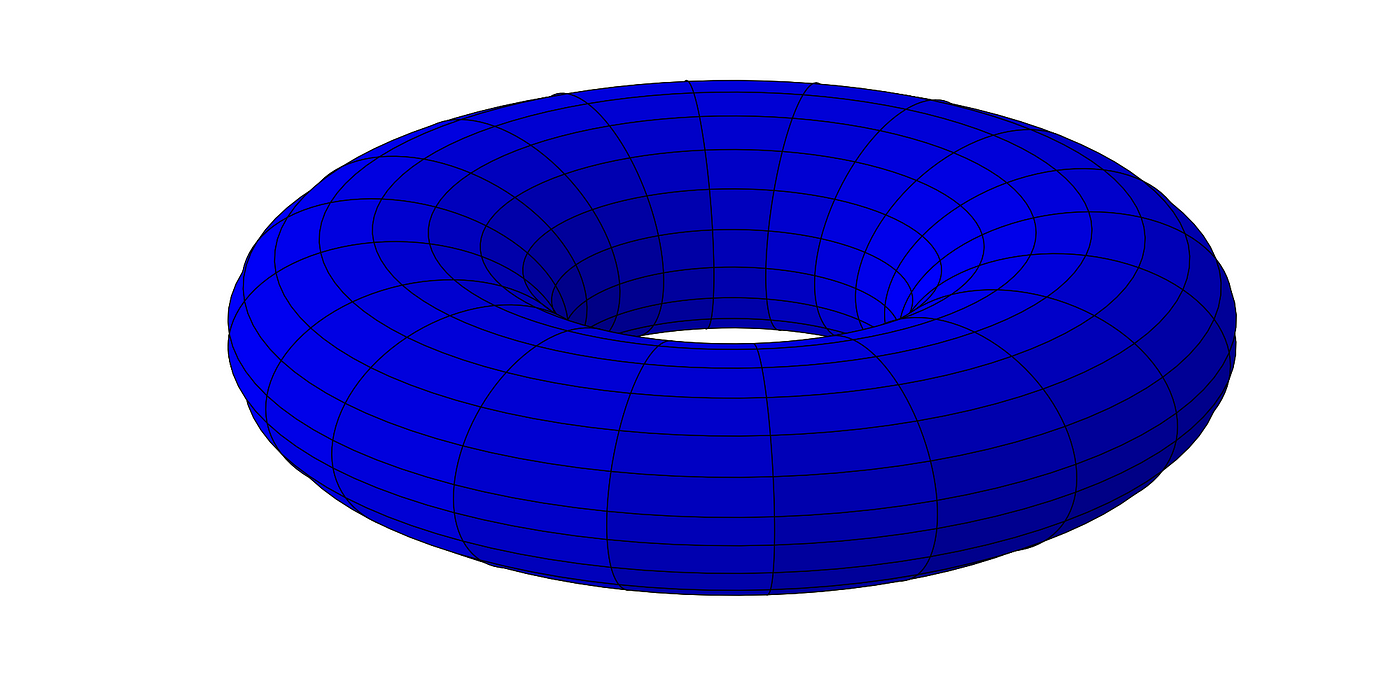
There is so much more that can be discussed like nearly-Hamiltonian systems, where Henri tries to stay on the same contour line but is tired and so slips downhill a bit regardless. Or stochastic differential equations, where Henri is drunk and can’t quite follow instructions too well. The particular area I am studying is when Henri lives on a doughnut and we want to know what kind of bifurcations we can be guaranteed to expect in nearly-Hamiltonian systems.

Dynamical systems model the world around us: predator and prey populations fluctuate in periodic orbits. Neurons fire in accordance with a specific kind of bifurcation. Artificial intelligence works by applying steepest descent algorithms. Galaxies move in accordance to Hamiltonian systems. The entire universe is one big dynamical system.