In the Deep Learning (DL) age, more and more people have encountered and used (knowingly or not) random matrices. Most of the time this use is limited to the initialization of the networks weights, that can be accomplished with a single line of code in your favorite DL framework. However, Random Matrices have a rich mathematical theory with far reaching applications in physics, network theory, machine learning, finance, etc. This fascinating range of applications also means that each field often developed its dedicated terminology to describe the same mathematical concept, often with confusing consequences. The aim of this article(s) is to introduce Random Matrix Theory (RMT) from a physicist's perspective while trying to relate different tools and terminology, especially across the math and physics literature. Although you do need to know basic calculus, I will try to introduce new concepts and give references in case you would like to go deeper.

This post is complemented by a numerical analysis you can find in this GitHub repository in Jupyter notebook format. Some of the content of the notebook is also presented in the last section.

Some Background

Historically, random matrices were introduced in statistics by John Wishart (1928), and saw their first appearance in physics when Eugene Wigner [1] used them to model the nuclei of heavy atoms (1955). You may know that at the microscopic level, where quantum mechanical effects are dominant, the energy spectrum of an atom is not continuous, but comes in discrete energy levels. Evaluating these levels for complex atoms comes at an expensive numerical cost on modern computers, but it was basically impossible to evaluate at the time Wigner was looking into the problem. Instead, he conjectured that these spectra could be akin to the eigenvalues of a random matrix, whose properties should only depend on its symmetry class (more on this later). This is an example of universality: complex systems that differ at some microscopic scale, tend to have similar properties at a “macroscopic one”. Moving from "micro to macro", many details are washed out from the description of a system, and the remaining relevant degrees of freedom tend to be common to a larger class of systems that share some particular symmetry. This idea of symmetry classes in RMT was further developed by Freeman Dyson [2]. There are three classical RM ensembles: orthogonal, unitary and symplectic; Dyson refer to them as the threefold way. If all of this sounds a bit obscure do not worry, we will come back to this later on.

A refresh of few key concepts in linear Algebra

Before diving deeper into RMT, let me recap some basic concepts of standard matrices. The purpose of this section is to define terminology, introduce the basic tools we will work with and refresh your memory in case you forgot some of these concepts. In doing so I will make no attempt for a thorough explanation, but I will assume some basic knowledge of calculus and linear algebra. Consider an N×N matrix M; the typical problem setup is:

where x and b are two vectors: the former is the variable we want to solve for and the latter a “source” term. You can think about this formula as a compact way to represent a system of coupled linear equations. A typical problem in linear algebra is to find the eigenvalues and eigenvectors of this matrix by finding the roots of the characteristic equation:

where λ are the eigenvalues and I is the identity matrix (in the equations I will use a hat to denote a matrix). From here, we can find the matrix U that diagonalizes M, i.e. M = U 𝚲 U^(-1), where 𝚲 = diag (λ1, λ2, …, λN). Note that M could have a rectangular shape, i.e. be an M × N matrix, in which case the so called singular values need to be evaluated; although these rectangular matrices are not very popular in physics, they are prominent in Machine learning (input data, weights, etc…) or finance, but more on this in a follow up post. The N eigenvalues of M form its “spectrum”, containing many important information about the system. For example, as mentioned in the introduction, they can describe the energy levels of a quantum mechanical system.

It is often convenient to evaluate the spectrum of M using the resolvent method; this method has the advantage of generalizing quite easily to infinite dimensional spaces, and can be used to solve non-homogenous, linear or non-linear differential equations. In this latter context, the resolvent is known as the Green’s function, and it is one of the central objects to evaluate when doing calculations in quantum field theory, see e.g. Ref. [4] for a general introduction. Going back to Eq.[1], we want to solve x = M^(-1) b. This inverse operator is represented by the resolvent:

The idea is that the resolvent has poles (i.e. singularities) located at the real eigenvalues of M. We can then use the toolbox of complex analysis by defining z= λ + i ε, such that the singularities are moved away from the real axis by an infinitesimal amount ε. This procedure is generally known as regularization. The (normalized) trace of the resolvent is known as the Stieltjes transform of M in the mathematical literature, and it is a very familiar object for physicists:

where we have defined the eigenvalues distribution ρ(λ), also known as the density of states in quantum mechanics. Here δ(.) is the Dirac delta function, see Ref.[5]. Our final task is to evaluate the eigenvalue distribution of the resolvent and hence the matrix M. The last bit of information we need is how to link the eigenvalue distribution to the trace of the resolvent, that is by using the Plemelj formula, see Ref. [4]:

In the random case, the entries of M will be sampled from a distribution, so the above object needs to be averaged over all possible realizations of M. Once the average of Tr[G(z)] is evaluated, we will analytically continue the result, i.e. use z → λ + i ε, take the Imaginary part and than the limit ε → 0^(+) at the end (the + sign means that we are approaching 0 from the positive real axis). In the next section we revise few key concept from probability theory that will be useful to accomplish our task.

A refresher of few key concepts in probability

This section is meant to refresh few concepts from probability that will be useful to understand the next section. I assume you are familiar with the concept of a random variable x. Depending on its domain, x can assume a series of values depending on the underlying probability distribution P(x). Say x denotes the position in space of an object, than P(x) will be the probability of the object to be at position x. A random matrix X is an extension of this concept; you may think about it as a collection of random variables. We may have two objects located at positions x1 and x2; in general, the two positions may not be independent, so we need now a joint probability distribution to describe our problem. If the two objects are independent then:

that is one of the fundamental properties satisfied by the probabilities of two independent random processes. Think about the most common of the examples, rolling a dice. The probability that say number 3 comes out in one roll is 1/6; the probability that we get two consecutive 3 is 1/6 × 1/6 and so on. This is not true if the two events are correlated, i.e. if they can influence each other. So the positions of the two objects may not be independent, but once we observe one, we can ask what is the probability that the second object is in a certain position given the fact we observed it in another; mathematically this is denoted as:

where the | expresses the conditional statement. To see how this is connected to random matrices, let me show an explicit representation of the two above equations, assuming that the random matrix X is Gaussian but bearing in mind that those two relations above are valid in general. To be explicit, X is a 2 × 2 matrix with unitary variance:

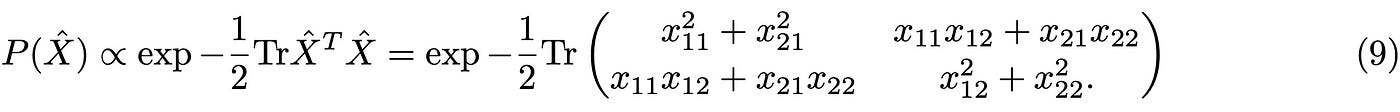
Note that I am using Tr as a shorthand for a sum over all indices; this is not the usual definition of the trace (sum over diagonal elements) but it is often used in the physics literature. From Eq.(8) we see that even if the single elements of the RM are i.i.d. (independently, individually distributed), the RM itself encompasses a certain degree of correlations due to the presence of the off-diagonal terms. If the latter are zero, we clearly have:

On the other hand, we can rewrite the matrix distribution in terms of its elements as a conditional probability:

The second objects I need to briefly introduce are the moment and cumulant generating functions. The former is defined as:

where x is a random variable, P(x) its probability distribution and ξ a parameter used to generate all the moments. In physics, this parameter goes under different names, depending on which field you are working in, but usually goes under the name of source term. Formally, you can obtain all the moments of the function by repeatedly differentiating with respect to ξ:

However, it is often more useful to work with the cumulants, as they often simplify calculations; The cumulant generating function is defined as:

How does this connect with RM or statistical mechanics? The central object of statistical mechanics is the partition function of the Boltzmann distribution (see below). In order to obtain average physical quantities we introduce a source term ξ and differentiate with respect to it. However, as we need a properly normalized quantity, we take the average of the logarithm of the partition function, that is the cumulant generating function defined above. You can generalize this concept to matrices or even functionals, as it is done in quantum field theory … but this is beyond the scope of this article:)

Bringing it all together

In this section I will give a “dirty” evaluation of the eigenvalue density. Although this evaluation gives the correct result, it hides several subtle points I will only briefly mention for now. I will follow a statistical mechanics approach, mostly focused on the calculation side. Also, we will focus for now only on the simplest of the RMT ensembles, the Gaussian Orthogonal Ensemble, or GOE for simplicity. Matrices belonging to this ensemble all have elements that are Gaussian variables; the other condition is the symmetry class under which these matrices are invariant, rotational invariance. Let be O an orthogonal matrix, then O^T = O^{-1}, where the superscript “T” stands for the transpose operation. This matrix acts on the elements of a matrix M and rotates them. For example, in two and three dimensions these matrices have the known form:

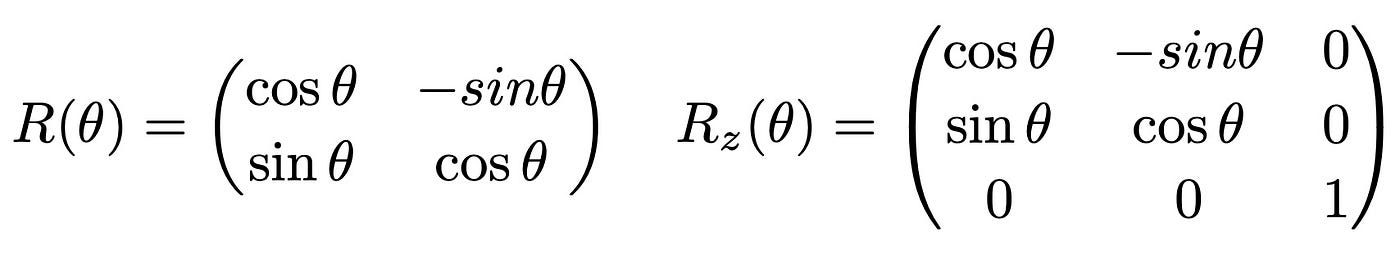
where the suffix “z” in the three dimensional matrix means that rotations are performed around the z axis.

What does it mean for M to be rotationally invariant? The rotated matrix M’ = O M O^T and M have the same eigenvalues but rotated eigenvectors w= O v. So the spectrum of M’ and M is the same. The first step in the calculation consists in manipulating the trace of the resolvent as follows:

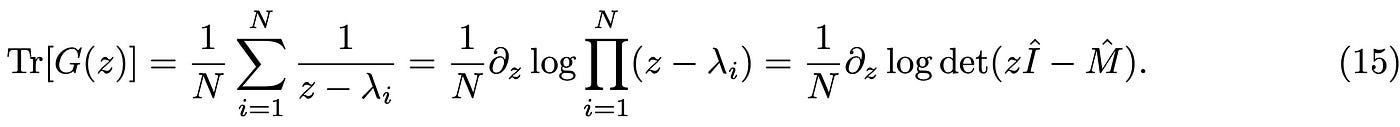
Looking at the above expression you may think we have taken a step back instead of forward! The idea is, however, to rewrite the trace of the resolvent as a more familiar object in statistical mechanics. Consider the following m-dimensional Gaussian Matrix integral:

the idea is to use this identity “backwards” to rewrite:

where Z now has the form of a statistical mechanics partition function for a specific realization of M and the measure 𝒟 𝜑 = ∏ d𝜑/(2 𝜋)^(N/2), where the product runs over i=(1,2…,N). So far, we have just performed some formal manipulations to massage our initial expression in a form that can be treated using the tools of statistical mechanics. We can also identify F_N(z) =- 1/N log Z(z) as the free energy of the system (with inverse temperature β=1/T); note that from a probability point of view, this is the (average) cumulant generating function defined in Eq.(14). At this point we need to average the trace of the resolvent over the different realizations of M using the rotationally invariant, Gaussian probability distribution:

where the first term on the right hand side is a normalization constant and we have used a unit standard deviation scaled by N as σ = 1/√N and zero mean. This brings us to the first (and only for this post) subtlety I mentioned before: when we take the expectation value of the trace of the resolvent in Eq.(17), we need to evaluate < log Z_M >_M, where < . >_M denotes the expectation w.r.t. M. The problem is: how do we evaluate the expectation value of the logarithm of a function and what is its meaning? A detailed answer to this question will be given in a follow up post, for the moment let me state few facts here without proof:

• < log Z_M >_M and log <Z_M >_M are known respectively as the quenched and annealed averages.

• For classical Random Matrix ensembles, it turns out that <log Z_M >_M = log < Z_M >_M; the results presented here does give the right answer within a simpler calculation scheme. However, it is not clear why these two type of averages should be equal (or different) for now.

In what follows we evaluate the annealed average of the partition function. In order to get all pre-factors right, is it convenient to write everything in components and separate the diagonal from the off-diagonal part. In doing so, we use the fact that for a symmetric matrix X we can separate the sum over the elements as:

where the second summation spans only the upper triangular part of the matrix and the factor of 2 accounts for the fact that the matrix elements in the lower triangular part are identical. Using this property in both the probability distribution and the resolvent, we can take the expectation value of the diagonal and off-diagonal elements separately and then sum back the two components as follows:

Pay attention to the newly generated non-gaussian term in the exponent proportional to 𝜑⁴; In a physical theory, this term would appear to describe interactions of some sort, e.g. a density-density interaction between “spins” at site i and j. More in general, this term describes how the fluctuations of 𝜑 (the variance) at site i are correlated to those at site j. In order to decouple this term we introduce an additional parameter that plays also the role of the order parameter in statistical mechanics. You may think about this as a change of variable in the integral or a generalized Hubbard-Stratonovich transformation in condensed matter theory. The idea is to use the delta function to enforce the scalar “constraint”:

Before jumping into the calculation, let us understand what this parameter means. Certainly, it redefines a quadratic variable as a linear one. Its meaning however, is to measure the fluctuations of 𝜑 at site i; clearly, this is not a simple change of variable! Order parameters are central objects in statistical mechanics and quantum field theory, as they are used to study transitions across different phases of the system.

This definitely looks better than our initial expression! In the second line of Eq.(23) we have used the Fourier representation of the Dirac-delta and introduced in this way the scalar Lagrange multiplier ξ [6]. This looks like a neat trick, but it is an incredibly useful and far reaching way of enforcing constraints in statistical mechanics and quantum field theory, where in the latter the delta becomes a functional that can be used, e.g. to regularize Gauge theories [7]! Before proceeding, it is convenient to redefine the Lagrange multiplier as follows: η = 2 i ξ/N and perform the Gaussian integral over 𝜑:

In case you wonder, the log η term comes from re-exponentiating the result of the Gaussian integral over 𝜑. We are interested in solving these two integrals in the limit of large N, i.e. we are looking for a continuous approximation to the eigenvalues density. In this limit, the evaluation of the two integrals becomes particularly simple, as we can use the steepest descent method [8]. If you are familiar with the concept of mean-field theory in physics, the steepest descent gives you exactly this result (for the moment just keep this in mind, I will come back on this in another post). The idea is to evaluate the integral in the stationary points of ℒ(η, q):

This gives a quadratic equation for q and therefore two stationary points:

As it is often the case in physics, only one of the two solutions makes sense; in this case we will select the solution giving a finite result. We can now use q* to evaluate the result of the integral and finally the trace of the resolvent in Eq.(15):

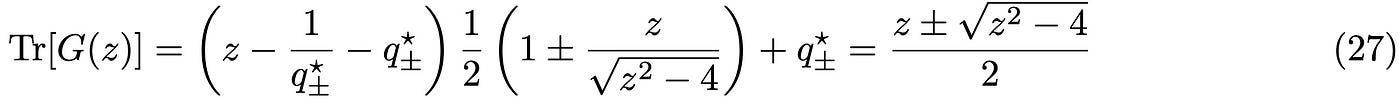
Note that the factor of N in the definition of the trace of the resolvent cancels out with our solution and we obtain a finite and N independent (remember this is a continuous approximation) result. In order to obtain the eigenvalue density, we need to perform first the analytic continuation z → λ + i ε, take the Imaginary part and then the limit ε → 0^(+). Note that the order of these operations is important! The tricky part is the imaginary part appearing in the square root; rather than having isolated poles, the square root has a branch-cut in the complex plane. A neat and simple way to take care of this problem without using advanced complex analysis is given in Ref. [3] by means of the following identity:

where I have defined:

Using this result back in the definition of the eigenvalue density, and taking the ε → 0^(+) limit, we obtain:

From a direst inspection you can see that if |λ| > 2 the spectrum is zero (this is a real function!), while is it finite for |λ|<2. As the spectrum is defined as a positive quantity, the sign of the solution should be chosen as + for positive λ and - otherwise. We finally obtain the celebrated Wigner semicircle law:

So much sweat for such a little formula :) In the next section I will plot the above expression against an explicit numerical evaluation.

Numerical experiments

To conclude, we check results against a direct numerical evaluation. Details can be found in this Github repository, here I will go through the main steps only.

At the time Wigner solved this problem, it was probably prohibitive to check results numerically if not via lengthy processes on some gym-room size computer. Nowadays you can evaluate explicitly these expressions on your laptop and check they agree with the analytical results.

One of the problem you face when running simulations is the finite size of the system. Remember that Eq.(31) has been obtained in the limit of large N. But how large is large? How big our simulation needs to be in order to agree with the analytical formula? To answer this question, let us write a function to perform the all evaluation:

The pseudo code is as follows:

1. Generate an N×N matrix instance X by sampling from the normal distribution with mean zero and variance σ = 1/√N.
2. Create a symmetric version of the matrix using: Xs = (X+X^T)/√2.
3. Get the eigenvalues using numpy.eigvalsh(Xs) note that this is a numerically optimized method to obtain eigenvalues of symmetric matrices.
4. Repeat n_samples times in order to sample different realizations of X.

For a small 10 ×10 matrix you will find something line this:

You can see two things here: one is that the tails of the numerical distrbution exceeds the domain [-2,2] of the bulk semicircle. And two is that the bins do not agree too well with the analytical expression. We can reperat the evaluation for N=500:

You can see that the results gets definitely better. We can evaluate the error between the analytical and numerical values as a function of the matrix size. Here I compute the Root Mean Square Root error (RMSE):

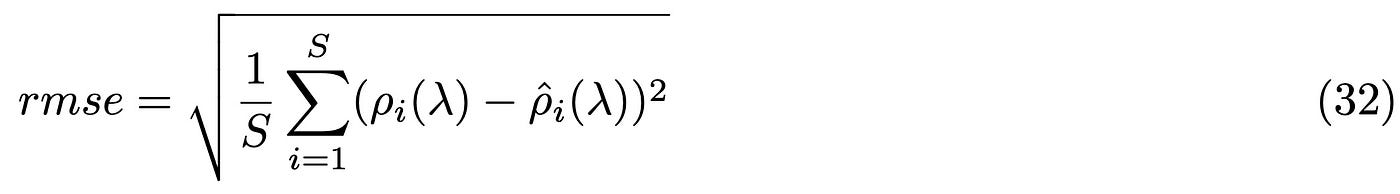
In the above equation, the first eigenvalue density is the one evaluated numerically, while the second is the expression we have evaluated analytically, while S is the number of samples. In the plot below I separate the tails from the bulk error:

You can see how the error goes down to ~ 0 (you can add more points to get a better result here) as the matrix size increases, providing in this way a nice numerical validation of our calculation above.

Closing remarks

In this article I presented a simple step-by-step introduction to Random Matrix theory, and in particular the Gaussian Orthogonal Ensemble. The calculation I presented is not the standard one you will find in books, the reason being that some of the steps I performed, e.g. the annealing average, are difficult to justify in this way. I will present a more standard derivation based on the so called “Coulomb gas analogy” in a follow up article. Another standard way of evaluating the quenched average is using Replicas [9], the introduction and justification of which needs a space of its own.

Hope you enjoyed this first look at random matrices and please leave comments and questions in the comments.

References

[1] E. Wigner, Characteristic vectors of bordered matrices with infinite dimensions, Annals of Mathematics. 62 (3): 548–564 (1955).

[2] F.M. Dyson, The threefold way. Algebraic structure of symmetry groups and ensembles in quantum mechanics, Journal of Mathematical Physics. 3 (6) (1962).

[3] G. Livan, M. Novaes, P. Vivo, Introduction to Random Matrices Theory and Practice, arXiv:1712.07903v1 (2017).

[4] M. Stone, P. Goldbart, Mathematics for physics, Cambridge University Press (2010).

[5] If you have encountered the Dirac function before, you know that this is really a distribution; otherwise I suggest to read this medium post.

[6] In case you are not familiar with the use of Lagrange multipliers for evaluating optima of a constraint system, have a look at this medium post.

[7] In the context of Gauge theories, this is known as the Fadeev-Popov method, and the lagrange multiplier fields as ghosts.

[8] If you are not familiar with this method, have a look here; for integrals defined in the real space, this method is known as Laplace’s method, while it goes under different names for integrals in complex space, e.g. saddle point, stationary-phase etc.

[9] M. Mezard, G. Parisi and M. A. Virasoro, Spin Glass Theory and Beyond, World Scientific, Singapore (1987).

Additional References

The standard book for Random Matrix theory is the one by Mehta:

• M.L. Mehta, Random matrices (Academic press, 1967)

I found this book difficult to follow for an entry level approach, but it contains a lot of advanced material. A more friendly introduction is provided in Ref.[1]. Another good introduction, with some interesting analysis of the underlying geometry of RMT is provided in:

• Yan V. Fyodorov, Introduction to the Random Matrix Theory: Gaussian Unitary Ensemble and Beyond, arXiv:0412017v2

Finally, for the mathematically inclined reader, I recommend Terence Tao’s lecture notes:

• Terence Tao, Topics in random matrix theory