Geometrical Beauty: The Properties of the Tautochrone Curve

The discovery of the form of the tautochrone, “the curve for which the time taken by an object sliding (without friction) in a uniform gravitational field to its lowest point is independent of its starting point,” was made in 1659 by the Dutch physicist, mathematician, astronomer, and inventor Christiaan Huygens. Huygens is widely regarded as one of the greatest scientists in history.

The Cycloid

His geometrical proof that the curve described above is an inverted cycloid (see the definition below) was published in his book Horologium Oscillatorium: Sive de Motu Pendulorum ad Horologia Aptato Demonstrationes Geometricae (“The Pendulum Clock: or geometrical demonstrations concerning the motion of pendula as applied to clocks”) published in 1673. The Horologium Oscillatorium isconsidered one of the three greatest works on mechanics in the 17th century, together with Galileo Galilei’s Discourses and Mathematical Demonstrations Relating to Two New Sciences (1638) and Isaac Newton’s Philosophiæ Naturalis Principia Mathematica (1687).

The cycloid is by definition, the curve traced by a point on a circle as it rolls along a line. It is the red curve shown in Figure 2.

Interestingly, this property of the cycloid was mentioned in Herman Melville’s book “Moby Dick” (1851) in the following passage: “[The try-pot] is also a place for profound mathematical meditation. It was in the left-hand try-pot of the Pequod, with the soapstone diligently circling round me, that I was first indirectly struck by the remarkable fact, that in geometry all bodies gliding along a cycloid, my soapstone, for example, will descend from any point in precisely the same time.”

Calculating the Time

We will now use basic calculus techniques to prove that the tautochrone curve is an inverted catenary. After Huygens’s proof, the conjecture was demonstrated by many other prominent mathematicians (including, among others, Lagrange and Niels Henrik Abel) using different techniques. This section will be based on Simmons.

Suppose the bead is released from rest. The law of conservation of energy gives us (the variable y is shown in see Fig. 5):

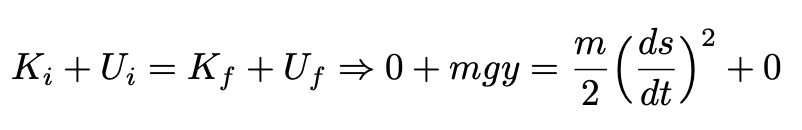
K and T are respectively the kinetic and potential energies of the bead (at the origin O and then at some non-specified y). As will be shown shortly, the beads released at O, A, and C (Fig.5) will arrive at B simultaneously.

Using the infinitesimal version of Pythagoras theorem,

and isolating the time variable, the right-hand side of Eq. 1 becomes:

where τ was chosen to represent the time the bead takes to go from O to (x,y).

Substituting Eq. 4 below (the parametric representation of a cycloid)

in Eq. 3 and then canceling the (1-cos θ) factor, a trivial integration gives us:

Now, we need to prove that τ is independent of θ. In order to do that we use the following equation from basic kinematics:

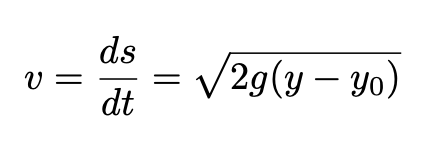
and change θ for (θ-θ₀). The interval τ becomes:

Now making the substitution

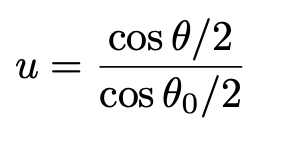
we obtain the integral of the inverse of the sine function which is trivial.

Our final result is then:

We, therefore confirm, as expected, that the time it takes for the bead to slide down a cycloidal wire is constant and does not depend on its initial position (see Fig. 6).

Thanks for reading, and see you soon! As always, constructive criticism and feedback are always welcome!

My Linkedin, personal website www.marcotavora.me, and Github have some other interesting content about math and physics and other topics such as machine learning, deep learning, finance, and much more! Check them out!