How e can rise from combinatorics

The constant e has a significant role across mathematics from growth problems to compound interest and even eigenvalues problems.
e has many representations, some of the most well known are

If the above formulation seems unfamiliar or daunting to you, don’t get discouraged since it’s not gonna be relevant for this article. In this article, I will discuss a totally different approach to how we can get an approximation of e by solving a simple and intuitive combinatorics problem.

We’ll start with a lighter version of the problem we are going to solve.

The Gaming Problem

You and your 3 friends have gathered for an evening of games on your favorite console. After playing for a while, your food delivery arrives and you all leave your controller randomly on the table. When coming back to play, nobody remembers which controller was his so everybody just picks one randomly, what are the chances that no one have picked the controller he played before?

To solve this question, first let’s assume that you and your friends have generic names like A, B, C, D for example and each controller has a number 1, 2, 3, 4.
Now we will have to calculate two things:

• How many permutations there are?
• How many permutations represent that nobody picked his controller?

There are 24 permutations in total:

Note that the permutations ‘ABCD’ for example denotes that person A got controller 1, B got controller 2, C got 3 and D got 4.

Following this symbolics, which permutations represent that nobody picked his controller?

Assuming that before you left your controllers on the table the permutation that represented the mapping between you and the controllers was ‘ABCD’, the permutations that represent that no one picked his original controller are

Now we can answer our question. Since there are 9 derangements out of 24 permutations we can say that the probability for a derangement is 9/24.

By now, you might still not have a clue about how all of it is related to e; try and calculate 24/9 this time and think what am I about to write next.

This time let’s leave our favorite console aside and answer the following question:

The Postman Problem

Say a postman has n letters and every one of these letters is addressed to a different person. Assuming that our postman is a bit clumsy and he delivers the letters randomly, what are the chances for derangement? or in other words, what are the chances that no one will get a letter which is addressed to them?

This time, we need to solve this question for every integer n so we can’t just write down all the possible permutations as we did before — and that’s where the inclusion-exclusion principle comes in handy.

Let’s start off by defining

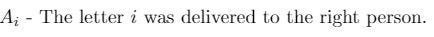
Then what we actually wanna know is the size of the following set

Using De Morgan’s law we can state that

Now the only thing I am gonna assume is that you know what is the inclusion-exclusion principle.
If you aren’t familiar with this principle you can find an explanation here (reading the first paragraph would suffice).

The statement of this principle is the following

I know it might seem a bit overwhelming at first but it’s a piece of cake, maintain your focus for a little longer and we’ll do this together.

Let’s go through one element at a time, starting with

There are n sets in this summation, and all of them have the same size — can be inferred from symmetry.
Ai resembles that the letter i was delivered to the right person, so how many permutations can we create if that’s the case?
We have n-1 letters to deliver and every order of these letters is valid so we can state that

Just as a quick reminder

Moving on to the next element, we will now calculate

Let’s take for example A1 and A2 and calculate the size of their intersection.
A1 means that letter 1 was delivered to the right person and A2 means the same for letter 2, meaning that there are n-2 letters left to deliver and every order of them is valid, then the size of the intersection is (n-2)!.
Then we can state that

Let’s now generalize this calculation and state that

Then we will substitute this in the principle’s general form

We are almost at the end, a few more mathematical simplifications will get us

What we got is “The number of permutations which are derangement with n letters”.
Since we want to know what is the probability of derangement, we will simply divide this result by n! (The total amount of permutations).

The last summation might be a bit familiar, it’s the sum expansion of e^x with x = -1

Then, we can finally state that for n that approaches infinity

Conclusion

Starting off with an intuitive combinatorial problem that seems completely unrelated to e, we managed to give rise to one of the most significant constants in mathematics