In this article, I will consider the problem of finding the shape of the free surface of the water inside a half-full bucket rotating with constant angular speed. Since I will work with systems moving with speeds much smaller than the speed of light, relativistic effects can be safely neglected. The derivation will be based on the Newtonian laws of motion, first enunciated in Newton’s magnum opus, the Principia.

The Principia was first published in 1687, followed by two expanded editions in 1713 and 1726. An American edition appeared in 1846. Page 83 contains the statement of “Newton’s Laws of Motion,” as shown below.

This article is based on Knudsen and Hjorth, which I will henceforth call KH.

Kinematics in Accelerated Reference Frames

What are the equations of motion of a body, expressed in terms of coordinates in the reference frame S, moving arbitrarily with respect to the inertial reference frame I? 
Our first goal will be to find Newton’s second law expressed in the moving frame S. Note that any motion of S can be obtained by a combination of a translation of the origin of I and a rotation of S around an axis crossing its origin.

We first call R the position of a body of mass m with respect to I and r the position of the body with respect to S. To find Newton’s second law of motion in S coordinates we first need to obtain the relation between the acceleration in Iand S.

The velocity and acceleration vectors of m measured in the inertial coordinate frame are:

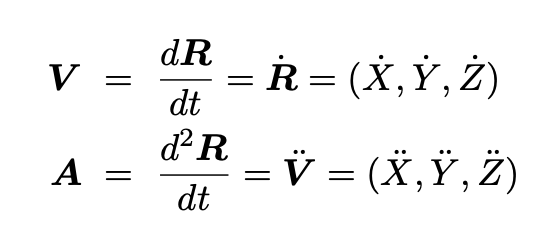
The velocity and acceleration vectors of m measured in the moving coordinate frame are:

Note that, since we are using Newton’s mechanics, the measure of time does not change from I to S.

As shown in Fig. 2, the position of the body in I can be written as:

Differentiating Eq. 3 twice we obtain, after some algebra, the following expression:

In this equation, a is the acceleration of the body with respect to S, the three terms on the right-hand side are, respectively:

• The relative acceleration between I and S.
• The acceleration of the body relative to the inertial frame I if the body is at rest at an instantaneous position (x, y, z) in S (this is the so-called comovingacceleration).
• The Coriolis acceleration.

The three components of a have the following form:

We can re-write the second and third lines of Eq. 5 using ω and dω/dt where ω is the angular velocity of the frame S:

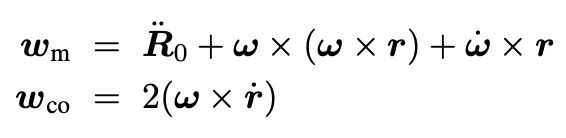
The second term (with an extra minus sign) in the comoving acceleration (the first line of Eq. 6) can be written as:

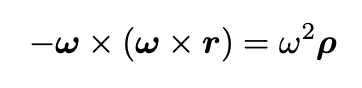
Dynamics in Accelerated Reference Frames

We will now express Newton’s second law as seen by an observer in the reference frame S. Following KH, we assume that the force acting on the body is the same in both reference frames. Hence:

which gives us Newton’s second law in S:

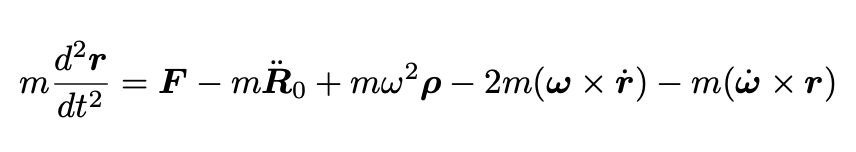
For Newton’s second law to be valid in S, we interpret the last four terms on the right-hand side of Eq. 8 as fictitious forces.

The Rotating Bucket

We now consider a bucket half full of water rotating with angular velocity ω about its symmetry axis. To find the shape of the surface of the water we proceed as follows.

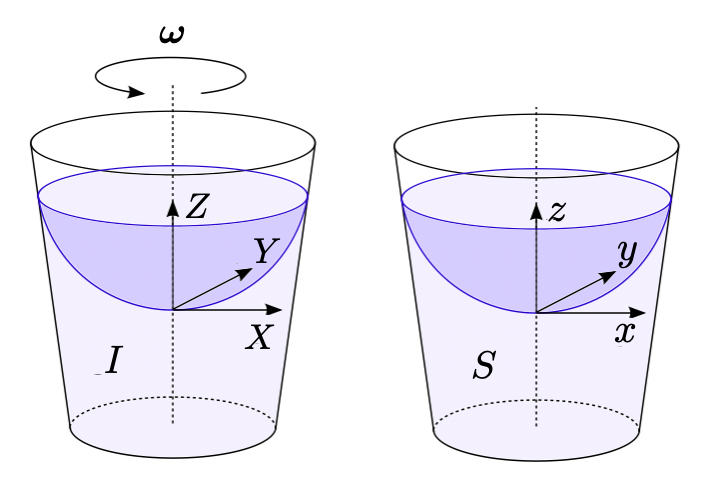
In the non-inertial reference frame S that also rotates with angular velocity ω, the bucket is at rest. After some time the water will come to rest with respect to the bucket.

Consider a water volume element, with mass m. The forces acting on it are:

• The gravitational force
• The centrifugal force
• The force originating from the pressure gradient

Since the mass is at rest in the rotating coordinate system S, the sum of these forces must be zero in S:

The double product in the second term can be rewritten as:

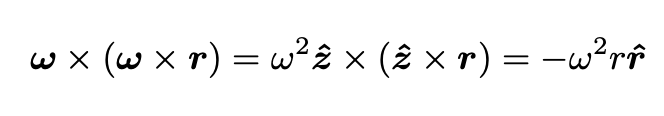
The components of the equilibrium equation are, therefore:

After integration, we obtain:

For a surface with constant pressure, Eq. 11 gives us:

We conclude that the shape of the water in the bucket is a paraboloid.

Thanks for reading, and see you soon! As always, constructive criticism and feedback are always welcome!

My Linkedin, personal website www.marcotavora.me, and Github have some other interesting content about physics and math and other subjects such as machine learning, deep learning, finance, and much more! Check them out!