Understanding Pierre de Fermat’s observation about prime numbers

If p is a prime and a is any integer not divisible by p, then p divides aᵖ⁻¹ - 1.

This property of numbers discovered by Pierre de Fermat in 1640 essentially says the following: Take any prime p and any number a not divisible by that prime. Say, p = 7 and a = 20. By Fermat’s little theorem, we then find that:

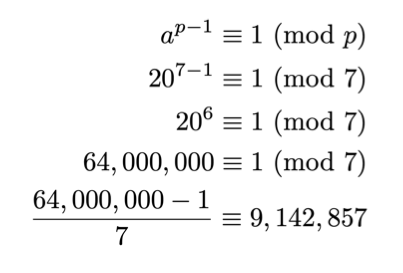
Now, we don’t care much about the actual number that results from this calculation. Rather, we care about the fact that without having to do the calculation at all, the theorem tells us that a whole number, an integer, has to result from it.

Introduction

Among Pierre de Fermat’s many correspondences with mathematicians around the world in the 1600s, the most consequential for number theory would be that which he shared with French mint official Bernard Frénicle de Bessy (1605–1675). As the story goes, de Bessy was renowned in France for his gift for calculating large numbers:

"On hearing that Fermat had proposed the problem of finding cubes that when increased by their proper divisors become squares, as is the case with 7³ + (1 + 7 + 7²) = 20², [De Bessy] immediately gave four different solutions, and supplied six more the next day."Excerpt, Elementary Number Theory (Burton, 2011)

De Bessy himself would later be best remembered for his publication Des quarrez ou tables magiques (“Finding the square equivalent of magic tables”), a treatise on magic squares published after his death in 1693, in which he provides all 880 different magic squares of order 4. A magic square is an n × n grid filled with distinct positive integers such that each cell contains a different integer and the sum of the integers in each row, column and diagonal is the same.

Although in no way Fermat’s equal as a mathematician, as a number theorist no contemporary could challenge Fermat like De Bessy (Burton, 2011). The correspondence between the two in the mid-1600s would result in some of the most striking discoveries in number theory, including the cube property of the number 1729 (now known as the Hardy-Ramanujan number, or taxicab number, for Srinivasa Ramanujan’s 1919 comment to G.H. Hardy that the latter’s taxicab number was “a very interesting number, […] the smallest number expressible as the sum of two cubes in two different ways”).

The most striking result of the correspondence between the two was however Fermat’s following statement in a letter dated October 18th, 1640:

Correspondence from Fermat to De Bessy (1640)
Tout nombre premier mesure infailliblement une des puissances – 1 de quelque progression que ce soit, et l'exposant de la dite puissance est sous-multiple du nombre premier donné – 1 ; et, après qu'on a trouvé la première puissance qui satisfait à la question, toutes celles dont les exposants sont multiples de l'exposant de la première satisfont tout de même à la question.

Essentially stating that “every prime number p divides necessarily one of the powers minus one of any geometric progression”. The result has since become known as Fermat’s Little Theorem:

Fermat's Little Theorem (1640)
If p is a prime and a is any integer not divisible by p, then p divides aᵖ⁻¹ - 1.

Fermat added “de quoi je vous envoierois la démonstration, si je n’appréhendois d’être trop long”, claiming, as he famously also did with his proposition of Fermat’s Last Theorem, that he would have sent De Bessy a proof of his claim “if I did not fear its being too long”.

Proofs

Nearly one hundred years later Euler would be the first to provide a proof to Fermat’s little theorem, in a 1736 paper entitled Theorematum Quorundam ad Numeros Primos Spectantium Demonstratio (“A proof of certain theorems regarding prime numbers”) in the Proceedings of the St. Petersburg Academy. However, it was later discovered that Leibniz had found virtually the same proof in an unpublished manuscript sometime before 1683, but that there is no way for Euler to have known about it (Burton, 2011).

Today, numerous proofs of the theorem are known. The proofs generally rely on two simplifications: First, the assumption that a is in the range 0 ≤ a ≤ p − 1. Second, that it is sufficient to prove that Fermat’s little theorem holds for values of a in the range 1 ≤ a ≤ p − 1.

Proof using the binomial theorem

Euler’s first proof (rediscovered after Leibniz) is a very simple application of the multinomial theorem, which describes how to expand a power of a sum in terms of powers of the terms in that sum:

The summation is taken over all sequences of nonnegative integer indices k₁ through kₐ so that the sum of all kᵢ is n. If we express a as a sum of 1s raised to the power of p (1 + 1 + 1+ … 1ₐ)ᵖ, we obtain:

If p is prime and kⱼ is not equal to p for any j, we have:

If p is prime and kⱼ is equal to p for some j, we have:

Since there are exactly a elements such that kⱼ = p, the theorem follows.

Proof as a corollary of Euler’s Theorem

Another proof of the theorem appears as a consequence of that fact that Euler’s theorem is a generalization of Fermat’s little theorem. It states that for any modulus n and integer a coprime to n (the only positive integer that divides both is 1), one has:

where φ(n) is Euler’s totient function, which counts the integers from 1 to n that are coprime to n. If n is a prime number, Fermat’s little theorem appears, as φ(n) = n − 1. A proof of the theorem hence follows from the proof of Euler’s theorem, which is typically done using group theory.

Proof using modular arithmetic

The following proof, using modular arithmetic, was originally discovered by James Ivory in 1806, before being rediscovered by Dirichlet in 1828.

Proof of Fermat's Little Theorem (Burton, 2011)
We begin by considering the first p - 1 positive multiples of a; that is, the integers a, 2a, 3a, ..., (p - 1)a. None of these numbers are congruent modulo p to any other, nor is any congruent to zero. Indeed if it happened thatr × a ≡ s × a (mod p), 1 ≤ r < s ≤ p - 1then, cancelling a on both sides would give r ≡ s (mod p), which is impossible because r and s are both between 1 and p - 1. Therefor, the previous set of integers must be congruent modulo p to 1, 2, ... , p - 1. Multiplying these congruences together, one finds thata × 2a × 3a × ... × (p - 1) × a ≡ 1 × 2 × 3 × ... × (p - 1)(mod p)meaningaᵖ⁻¹ × (p - 1)! ≡ (p - 1)!(mod p).Cancelling (p - 1)! from both sides of this expression, we obtainaᵖ⁻¹ ≡ 1 (mod p), which stated differently equals aᵖ⁻¹ - 1, Fermat's Little Theorem.

Proof using group theory

To prove Fermat’s little theorem using group theory, recognize that the set G = {1, 2, …, p − 1} with the operation of multiplication forms a group. Of the four group axioms, the only that requires effort to verity is the fourth, namely that the elements in G are invertible.

If we assume that every element in G is invertible, assume that a is in the range 1 ≤ a ≤ p − 1, that is, assume a is an element of G. Let k be the order of a, i.e. the smallest positive integer such that aᵏ ≡ 1 (mod p) is true. Then the numbers 1, a, a², …, aᵏ⁻¹ reduced modulo p, form a subgroup of G whose order is k. Therefor, by Lagrange’s theorem, k divides the order of G, which is p − 1. So p − 1 = km for some positive integer m, and:

To prove that every element b of G coprime to p is invertible, this identity can help us as follows. Because b and p are coprime, Bézout’s identity assures that there are integers c and d such that bc + pd = 1. Modulo p, this implies that c is an inverse for b, because bc ≡ 1 (mod p). Because b is invertible, so is every other element in G, and so G must be a group.

Several other proofs are available on Wikipedia.

Application: Primality test

Fermat’s little theorem would become the basis for the Fermat primality test, a probabilistic method of determining whether a number is a probable prime. If we for instance want to find out whether n = 19 is prime, randomly pick 1 < a < 19, say a = 2. Calculate n − 1 = 18, and its factors: 9, 6. We check by calculating 2¹⁸ ≡ 1 (mod 19), 2⁹ ≡ 18 (mod 19) and 2⁶ ≡ 7 (mod 19) and find that 19 must be prime.