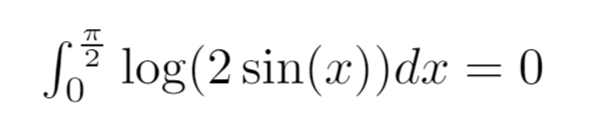
Let’s discover the ingenious, yet simple, solution to Euler’s Log-Sine integral

Tactics

First we give a label to the value of our integral, I.

Our approach will be to prove that I satisfies the equation I = 2I. This of course implies that I = 0 after subtracting I from each side.

To do this, we will need to find a clever way of representing I. The key insights will use the behaviour of sin(x), cos(x) and log(x) cleverly.

Below we outline some of the key properties of sin(x), cos(x) and log(x), so feel free to skip if you are already familiar with these or come back as needed.

Tactics: Properties of sin(x) and cos(x)

In this question, we express sin(x) and cos(x) using radians. Radians is a measure similar to degrees, but we have 2 pi radians in a circle. So 90 degrees = 360/4 is equivalent to pi/2 = 2*pi/4.

Recall that, for any number u, we have the following identity: [u is a slightly odd choice of variable name, but we use it later so it is good to get familiarity]

The graph will probably be enough to convince you of this. You can also draw a right angled triangle, as in the diagram below, to prove this.

The other important trig identity, the double angle formula is:

sin(2x) = 2cos(x)sin(x)

Tactics: symmetries of sin(x)

The next property we note is the how sin(x) is symmetric.

A consequence of this symmetry is that

This becomes apparent when you look at the graph of log(sin(x)).

Tactics: logarithms

One key property about the logarithm function is that

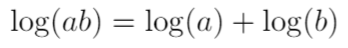
This is going to be very helpful, because it can be combined with the double angle formula:

Solving the Euler Log-Sine Integral

We now use a substitution

This gives a new integral in terms of (pi/2 — u). Next we use what we learned about the relationship between sin and cos:

So far, so good. But we want to evaluate I + I.

The difficulty here is that one integral is in terms of u and the other is in terms of x. The next manipulation may feel a bit uncomfortable, but the key thing to realise is that x and u are ‘dummy variables’. They represent something, in this case an area under a graph*, and so it doesn’t matter which variable name you use. So we change the du and the u to a dx and an x.

Optional note on variable switching. The key distinction to make here is that the value of an integral depends on the range we integrate over and the function. When we used the substitution pi/2 - u = x, the variable u wasn't the important part, what we were really doing was showing an equivalence between integrating the function sin(x) over a certain part of the x axis, and integrating the function sin(pi/2 - x). The u just helped us keep track of how the 'dx' needs to be scaled to keep the two integrals equivalent.

*side note: if you learn a more formal approach to calculus,as you would in a mathematics degree, the mathematical object is technically a limit of a sum. But for our purposes, the analogy with area under a graph captures the relevant information.

We now use our log rules:

We are nearly there! We do one more substitution

But, if you recall from the tactics section, sin(v) is symmetrical about pi/2. That meant that the following holds:

Cancelling the 2 divided by 2, this finally yields:

The only difference with our original expression is a different ‘dummy variable’. Like before, we can change v back to x and dv back to dx:

And we are done! Euler’s Log-Sine Integral is conquered!!

Let me know your comments, requests, thoughts and anything else below! I originally saw this integral in the simply wonderful book ‘Inside Interesting Integrals’ by Paul Nahin. It’s a really fun book I worked through last year, and I can thoroughly recommend it! You can follow me on twitter where I am ethan_the_mathmo for random math related thoughts and updates.