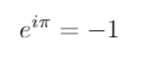
Here we investigate and understand the brilliant formula which unlocks the power of complex numbers.

First Impressions

In some sense, it is obvious why it is famous. Like, what! e raised to the square root of -1 multiplied by pi gives -1. How!??!! I remember being astounded that this was the case.

Yet this turns out to almost be a definition of complex numbers, the idea that we can write:

It extends the definition of e to make sense for complex numbers while still making sense with the definition of e for real numbers. This will all make a lot of sense later, but is mind-boggling at first!

First, let’s really understand the right hand side of the equation, which ties in beautifully with elementary geometry.

Visualising Complex Numbers

As a first pass, we can view complex numbers as a point on the 2D plane, described by a radius, and by their angle, or defined by their x coordinate, and y coordinate. The Y-axis corresponds to the ‘imaginary axis’, and the ‘X-axis corresponds to the ‘real axis’. So the points (2,3) corresponds to 2+3i, where i is the square root of -1.

Adding two complex numbers corresponds to just adding their real and imaginary parts. So, for example, (2+3i) + (1+5i) = (3+8i)

Multiplication can be visualised in an interesting way: it corresponds to a rotation and a change in radius. Here, the square root of negative 1 makes perfect sense, as we have extended the definition of multiplication! The point i has angle 90 degrees, and length 1. So, when we multiply a point z by i, we rotate it by 90 degrees, and scale the radius by 1. Of course, scaling a radius by 1 leaves it the same. If we were to multiply z by 2i, then it would be rotated by 90 degrees, and stretched outwards by a factor of 2.

Now we do something a little cheeky. Let’s use the rules for e defined for real numbers on complex numbers too, and see how pretty things turn out! Let’s multiply two numbers together. However, we do something a little… weird. We write our complex number in the form below. (This will make more sense later!!)

We first show these on the complex plane. z_1 is the blue line, with a larger angle and radius, and z_2 is the red line, with the smaller angle and radius.

Now we multiply them together, both showing what is happening visually and algebraically.

Visually when we ‘multiply’ the red and blue lines (or ‘vectors’), we get the purple line.

In complex multiplication, we sum the angles and multiply the radii. The purple line’s angle is the sum of the red line’s angle and the blue line’s angle. The purple line’s length is the product of the red line’s length and the blue line’s length.

Now let’s see visually what happens to the purple line when we rotate the red line. The diagram below shows that its length remains the same, but the purple lines rotates by the same amount as the red line rotates!

Now, let’s formalise this with some algebra

In the above, we see we have two e’s multiplied together. Now we do something a little cheeky. We know that for real numbers that:

So we try our luck and use the same rule — which we haven’t formally justified! — for complex numbers.

So overall we get that:

So algebraically we get what we saw visually! To work out the product of two complex numbers, we sum their angles and multiply their radii.

e, sin, cos, and magic

Now let’s examine how we were writing complex numbers.

We could express it either in terms of a real part and a complex part, or we could express it in terms of a radius and an angle.

How can we relate those two?

We start with writing z = x + iy

Now, look at these two representations.

The picture on the left is writing our complex number as a sum of a real part and an imaginary part. The picture on the right converts this into writing these components in terms of cos and sin, using the normal definition from trigonometry.

Okay, this seems neat. And now comes the magic.

This is Euler’s genius. He extended the definition of e to work naturally with the operations defined on complex numbers. (Quite how brilliant his idea was will become clear if you do the optional section on power series!)

The most famous line in mathematics

Now, we take a look at perhaps the most famous line in all of mathematics.

Let’s unpack that using our new tools:

The formula highlights the beauty of Euler’s link between e and complex numbers, but in reality it isn’t that complicated to understand once we understand the definitions and notations. All we are doing is converting a number from its representation in terms of a radius and angle, to its representation as a real part + an imaginary part.

The story doesn’t end here. The formula hints at how magical the world of complex numbers will be. However, it would take 19th century mathematicians, especially Cauchy and Riemann, to unlock the secrets of calculus in the complex numbers.

Power Series — and extending the definition of ‘e’ (optional, but strongly recommended for the curious!)

Power series give a nice way to extend the definition of e, sin, and cos from their definition as a function from real numbers to real numbers, to their definition on the complex plane.

This shows that Euler’s definition really does mesh wonderfully with the definitions for real numbers.

e^x, sin(x), and cos(x) can all be defined as a power series.

This means that for every point x, the value of each of these functions can be evaluate by the infinite sums above. The ‘…’ means that the pattern continues indefinitely. I will only write the first few terms and then write the ‘…’ to avoid the screen being filled with an infinite number of terms from a power series!

Now, recall that i² = -1, is how we started looking at complex numbers. So why don’t we try the following

We need to simplify all the powers of i.

This pattern then repeats. E.g. i⁷ = i⁴i³ = 1(-i) = -i

So we simplify:

Ok! This seems promising. Now we separate real and imaginary parts.

Oh wow. This is very promising. Recall the power series definition of sin and cos? If I write a few more terms, and you remind yourself of the power series I wrote at the beginning of this section:

I’ll give you one last chance to spot it! ……(!!)

Amazing!

So it turns out, with our definition of i, and with our power series definition of cos and sin and e , the formula makes perfect sense. The geometric definition of multiplication of complex numbers not only looks cool but amazingly ties the value of e to cos and sin.

Epilogue

Who would have thought it! The functions created by the Greeks to describe coordinates on circles (cos and sin) have a mystical link with the function which differentiates to itself, e, once we expand numbers to include the square root of negative 1.

It’s a wonderful world.

Please leave your comments and corrections below! I try to read and respond to all of them, and adjust articles if people spot mistakes. If you are a twitter person, I occasionally post updates and problems I am working on there, where I am ethan_the_mathmo. Thanks for reading :)