Computer-Aided Engineering (CAE) is getting more and more important in modern engineering. FEM-programs, simulation tools and huge libraries are offered to the engineer who has to decide what suits his problem best he’s facing. But to make a good decision you have to know at least the basic principles of the algorithms used in the respective tool. Some of the following characteristics of a tool/algorithm might be useful to weigh up:

• accuracy
• computational demand
• flexibility

In a lot of cases, the engineer has to know the tradeoffs of the algorithm. One of the most common tradeoffs is accuracy vs. computational demand. So to evaluate the tool/algorithm you need a deeper understanding of the things happening in the background of the CAE-program. I’m going to present three algorithms from three different fields of engineering.

1. Jacobi Method -> FEM
2. Heun’s Method -> System Simulation
3. Gradient Descent -> Optimization

Jacobi Method¹

The Jacobi Method is used to solve systems of linear equations. Unlike the Gaussian Elimination Method, the Jacobi Method is iterative. Therefore the calculation itself performed on every iteration is rather simple. Another advantage is the fact that you can use parallel computing while implementing the algorithm.

Especially in FEM the Jacobi Method (or related algorithms) come into place to solve huge matrices. Figure 1 shows how the iterative representation of the Jacobi Method is derived based on the simple formulation of a system of linear equations (1).

What’s special about the Jacobi Method is the fact that matrix A is split into 3 matrices, which is called Splitting in mathematics (sometimes I can’t believe the overwhelming creativity of mathematicians). Matrix A is split into a Lower, an Upper and a Diagonal Matrix. The advantage gets clear when looking at (6). The inverse of a Diagonal Matrix is quite simple to calculate.

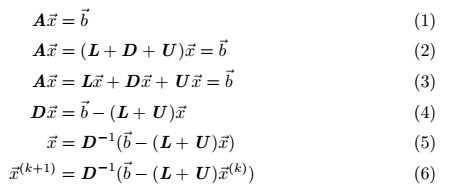
Figure 2 shows the same as (6) but this time representing it for a single element of our solution vector x.

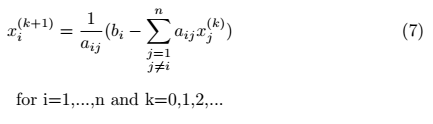
Figure 3 shows the Jacobi Method in action. I had to perform a FEM Analysis on this bridge construction in my FEM Lab last semester. Splitting Methods like the Jacobi, Gauß Seidel or Successive Over-Relaxation Method make this possible. But different methods can lead to different results. So you have to understand each method to optimize accuracy / computational demand.

Heun’s Method

Heun’s Method is used for numerical integration. Therefore it can be used to solve Ordinary Differential Equations (ODEs) which is a common practice in simulation tools like MATLAB Simulink. Whenever you model a System and express it via an ODE you can either solve it analytically or use numerical integration. Heun’s Method uses both, explicit and implicit, Euler Methods. Through a Predictor-Corrector Principle Heun’s Method is an explicit method. I won’t go much into detail here because I already wrote a story explaining the mathematics behind Euler Methods and Heun’s Method in more detail. I will link all my stories with regards to this in the Author’s note.

The given MATLAB Code below can be used to implement Heun’s Method for first-order linear ODEs. To use it, you have to define the derivative of the ODE and have to pass it to the algorithm (in this case the handle “yDot” which can be defined using @ in MATLAB). The output is the resulting answer of the system given by two vectors T and Y. The main part of the algorithm is just line 9 and 10. The relevant parameter is tStep defining the size of the increment in each iteration.

function [T, Y] = heun(yDot, tStep, tBeg, tEnd, y0) Y(1) = y0;
c = 1;

for i = tBeg : tStep : tEnd

T(c) = i;
Ypred = Y(c) + tStep*yDot(Y(c));
Y(c+1) = Y(c) + 0.5*tStep*(yDot(Y(c))+yDot(Ypred));
c = c + 1;

end

end

Figure 4 shows a solution to a more complex ODE higher order. This was created for a simulation project in university where we modeled and simulated an active suspension of a quarter-vehicle to optimize the dynamics of a Formula Student Race Car.

The System is stimulated via a Fourier Series that emulates the ground. The upper coordinate system compares the controlled and uncontrolled case. When the controller is on, the suspension is active and the hydraulic actuator works in series with the spring-damper-unit. When the controller is off, the actuator is completely stiff and acts as a rigid connector so the spring-damper-unit acts on its own.

The lower coordinate system compares Heun’s Method against the Runge Kutta Solver used in MATLAB Simulink as a standard (ode23 for you curious folks). However, Heun’s Method is a Runge Kutta Method. The solver used standardly by Simulink is just of a higher order. Runge Kutta Methods are a class of one-step procedures used for numerical integration. This should show you how different solvers can affect the result. It is always useful to do a quick study on how the solver affects the result to optimize accuracy / computational demand.

Gradient Descent²

Gradient Descent is an optimization algorithm for general optimization problems. You want to find the global minimum of a function with the input W. The input is a set of parameters that needs to be optimized to reach that minimum. This algorithm is commonly used in supervised Machine Learning especially in Neural Networks. The Loss L or Cost J respectively is just the difference between the prediction of the NN and the corresponding label in this case.

Figure 5 shows the update-rules for GD without (8) and with (9) a momentum term. The idea is to approach the minimum by subtracting the gradient of L(W) from W. Alpha is just a scaling factor defining how big the step is. If we approach the global minimum more and more it is obvious that the gradient approaches 0 and therefore the update of our new set of Parameter W_n+1 will be very small. At the global minimum, there will be no change at all.

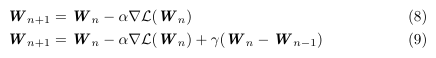
Figure 6 visualizes the idea of GD. When reaching the global minimum the gradient is 0 and no further change of W is the consequence. It’s that simple.

However, what if we have a function with lots of local minima? Then we can add the momentum term mentioned earlier. To avoid sticking in local minima, when the subtrahend is close to 0, an additional term is added to increase the change of W. This additional term called momentum is just the difference between the current set of parameters and the one before that. And again, Gamma is just for scaling purposes. To optimize convergence and accuracy it is important to understand the impacts of Alpha and Gamma. Also, GD is just one out of many different gradient-based optimization algorithms. Again, to optimize accuracy / computational demand a basic understanding of the algorithm is necessary.

Summary

In this part of engineering fundamentals I covered three different algorithms from three different fields of engineering:

1. Jacobi Method -> FEM
2. Heun’s Method -> System Simulation
3. Gradient Descent -> Optimization

The given examples should demonstrate why it is important to have a basic understanding of certain algorithms as an engineer and how this can affect your work. I hope I could motivate you to dive deeper into a topic even if it looks complicated at first sight.

Author’s note

Thank you for reading this far! If you have any thoughts, annotations, or ideas about this story feel free to leave a comment. If you are interested in the mathematical background of Heun’s Method or how to model systems like the active suspension have a look at my other stories and parts of engineering fundamentals.

References

1. Stürzekarn, M. (2005). Proseminar Numerik: Jacobi- und Hauß-Seidel-Verfahren, Jacobi-Relaxationsverfahren. (Summer Semester 2005). Hamburg: University of Hamburg
2. MATLAB-Documentation. (2021). Options for training deep learning neural network. [Online]. retrieved on 22th of February 2021 from https://www.mathworks.com/help/deeplearning/ref/trainingoptions.html