Do Masses of Fundamental Particles Follow Benford’s Law?

Humans like looking for patterns, be it shapes in the clouds or relationships among numbers. We are probably evolved to do so for survival, and just can’t help. In science, pattern recognition helps researcher to tell the shape of galaxiesor to identify the decay of short-lived fundamental particles such as top quarks. Especially in physics, scientists have been scratching their heads for years trying to come up with an explanation of the apparently random distribution of the mass of fundamental particles or at least those that belong to the theory of the Standard Model of Particle Physics. Is there an underlying mechanism that determines their value? Or, more disturbingly, do we live in a Universe where electrons, quarks and bosons simply happen to have masses that allow life-as-we-know-it to thrive? Are there other “sterile” Universes out there where these masses are different? To tell these ideas apart, a surprising property of random numbers called Benford’s Law may come to the rescue. But before we get into that, what is exactly the issue with particles’ mass?

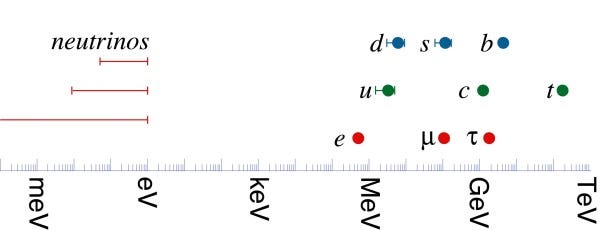
In the past 150 years or so, scientists have identified a number of objects (most of then extremely short-lived) that appear to be made of nothing else, which as usually referred to as fundamental particles. Three of them (electrons, up and down quarks) belong to a class called fermions and constitute ordinary matter. They appear to us most normally in the form of atoms. Beside matter, also forces (at least three of them) can be interpreted as large-scale phenomena due to the exchange of mediators, or more properly of bosons. The most familiar of them is called photon and is the particle light is made of. Finally, there is some sort of universal “liquid” called the Higgs field that permeates space. The interaction between all particles and the Higgs field determines the weight (one should better say the mass) of all elementary particles. Some of these masses turn out to be zero. Others are so diverse that they span several order of magnitudes in a unit called electronvolt (eV), roughly from 0,001 of the extremely lightweight neutrinos to 173 billions of the disturbingly heavy top quark. If you line up the masses of the particles on a scale, you would not be able to notice any specific pattern. They seem just completely random. This seemed outrageous to many physicists, who wouldn’t be satisfied until a proper explanation of how and why these numbers are what they are comes about.

Not that we lack explanations, some being more whimsical than others (my favourite being the Veltman’s hypothesis, i.e. that the sum of the squares of the masses of all fermions is equal to the sum of the squares of the masses of all bosons. Neat and likely completely wrong). The problem, in fact, is to determine a sort of litmus test to find the correct one or at least weed out most of them. However, one can ask a simpler question: are the masses random? Is there a test we can apply that helps us to determine whether God plays dice, or if there is an underlying mechanism we are not yet aware of? Here’s where Benford’s Law may come helpful.

When we study the physical world, we always seek an explanation for the things that happen (a supernova exploded because the star burned up all the hydrogen, antibiotics work because they kill bacteria), but when it comes to mathematics, things become much less obvious. Why is the ratio between the circumference and the diameter equal to 3.1415… ? Why does the limit of (1 + 1/n)^n as napproaches infinity becomes closer and closer to 2.71828… ? Some of these relationships seem to be simply ingrained in tables of numbers, and so is one that is truly remarkable. As the story goes, astronomer Simon Newcomb noticed that in books containing tables of logarithms, the earlier pages (that started with 1) were much more worn than the other pages. This led to the observation that in a set of randomly picked numbers spanning several orders of magnitude (10s, 100s, 1000s, etc.), about 33% of these numbers start with 1, 17.6% start with 2, 12.5% start with 3 and so on and so forth. The relationship was re-discovered and formalized later on by the physicist Frank Benford, who found it in disparate datasets including the area or US states, the length of rivers, and physical constants.

Albeit mysterious, an explanation for its existence is in fact relatively simple. If one considers numbers between 10 and 99, the fraction of numbers starting with a given digit (i.e. 1, 2, 3…) is equal. Moving to next order of magnitude (i.e. 100 to 999) the same is true, but there are 10 times more numbers between 100 and 199 than between 10 and 19. Going on, this relationship can be concisely expressed as a logarithm:

But then, what happens when the numbers we picked are not random? The answer is simple: they do not follow Benford’s Law. For example, phone numbers have fixed length and are not random. The last digit of rounded numbers is not random either and violates Benford’s Law, too. Sequential numbers (e.g. invoice identifiers) are not random either. Over the course of several years, Benford’s Law has become a tool to detect commercial and tax frauds exactly because numbers that have been fiddled with are not random.

So, the million dollar question is: does the mass distribution of fundamental particles follow Benford’s Law? If not, is that an indication that they are notrandom?

Luckily, that’s very easy to check. For those who are more inclined towards computer programming, I prepared a Google Colab notebook (follow this link) to explore this application of Benford’s Law. Particle properties are tabulated in a document called The Particle Data Group Handbook, but they are also accessible from the python library PyPI.

To test the randomness hypothesis, we create a list of masses and from them we calculate the frequency of the first digits (the frequency is the count of occurrences divided by the total number of elements, and is thus a fraction between 0 and 1).

MeV = 1.
GeV = 1000.M_quarks = [173*GeV, 4.18*GeV, 1.275*GeV, 95*MeV, 2.01*MeV, 4.7*MeV]
M_bosons = [125*GeV, 91.2*GeV, 80.4*GeV]
M_leptons = [1.78*GeV, 105.7 * MeV, 0.511*MeV]M_fundamentals = M_quarks + M_leptons + M_bosons

At this point, we can easily compare what we have obtained for the fundamental particles to the expected frequencies that come from Benford’s Law. It doesn’t take much to notice that the agreement is very poor, although qualitatively there are more particles whose mass starts with a 1 than any other number. Notably, there are no known particles whose mass begins with 3, 5 or 7.

So what does this all mean? We haven’t performed a truly statistical test to reject our randomness hypothesis (this is more the subject of a research paper than a post on a blog), but in my opinion we can give a couple of interpretations that are not too far fetched:

1. The masses of fundamental particles are not truly random, but there is an underlying mechanism we have not yet figured out;
2. We have not discovered all the fundamental particles. The missing ones would “fill the blanks”. This may be a hint of where physics beyond our knowledge may be found (e.g. in a mass range around 3, 5 or 7 TeV);
3. There simply too few fundamental particles, so whatever the result, we don’t have enough statistical power to draw any conclusion;
4. A combination of the above.

Only time and more data will tell! However, concerning the third point, we can do better. In fact, quarks are not found in nature all alone, but always appear as in doublets (mesons), triplets (baryons), or more “exotic” multiplets (tetra- and penta-quarks), which are collectively called hadrons. As mentioned above, the properties of these particles as they appear in the PDG handbook can be used in computer codes such as python scripts. In the case of hadrons:

!pip install particle

from matplotlib import pyplot as plt
from particle import Particle

M_hadrons = [p.mass for p in Particle.findall(lambda p: p.pdgid.is_hadron, particle=True) if p.mass is not None]

plt.hist(M_hadrons, bins=40)

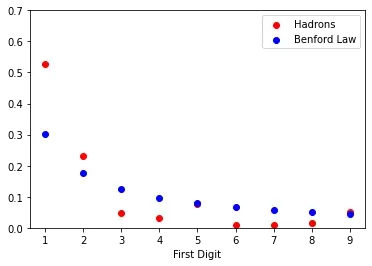
If we count the number of hadrons whose mass starts with 1, 2, 3, …,9, and calculate the frequency, we can compare this distribution to Benford’s Law.

Also in this case, the distribution agrees with Benford’s Law only from a qualitative perspective, i.e. there are more hadrons whose mass starts with 1, fewer whose mass starts with 2, and so on, but some digits are just missing as e.g. no particle whose mass in the order of 8 GeV exists (or has yet to be discovered).

To conclude, Benford’s Law is a relatively little known property of random numbers that has been under the spotlight recently, mostly to detect frauds. A very entertaining episode of the Netflix show Connected (I highly recommend to watch all the episodes) is dedicated exactly to this fascinating topic. We don’t know yet if Benford’s Law holds some clues to a deeper realm of reality, but I believe it’s an intriguing possibility that should be explored more thoroughly.