The Fibonacci Sequence is one of the cornerstones of the math world. Fibonacci initially came up with the sequence in order to model the population of rabbits. In reality, rabbits do not breed this way, but Fibonacci still struck gold. This sequence has so many beautiful mathematical features it has its very own journal dedicated to it — Link.

Before we move to Binet’s formula — let us take a look at the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144…

We notice that each term is a sum of the two before it, so we can define the Fibonacci sequence recursively:

The limitations of this formula is that to know what the 8th Fibonacci number is, you need to figure out what the 7th and 6th Fibonacci number, which requires the 5th and 4th Fibonacci number, and on and on, until you reach 0 and 1. So, Jacques Philippe Marie Binet set out with the goal to come up with a formula, for which you could plug in 8 and get the 8th Fibonacci number without knowing the numbers before it.

Intuition

My goal for this article is to explain how anyone of us could come up with this logically. So, let us start by trying to classify this sequence. The two most common sequences are — Arithmetic and Geometric.

Now, we can immediately disqualify this as an Arithmetic series because the difference between adjacent terms are strictly increasing. Now, to test to see if the sequence is geometric, we have to divide subsequent terms, to see if there is a common ratio. Let us take a look at a table of ratios-

Although the ratios of subsequent Fibonacci terms are not equal, but as n keeps on increasing, the ratio seems to converge to 1.618033988….

“Modified” Geometrical Sequence

At this point, we know it isn’t a conventional geometric sequence, but the further on we go into the sequence, the more geometrical it gets. For now, let us treat it like a geometric sequence and set up an equation to solve for the common ratio. That allows us to come up with the definition F(n)=kⁿ. Armed with this knowledge, turn the recursive definition into a polynomial equation. We start off with

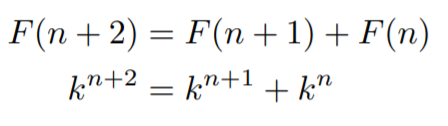
Since k≠0, we can divide both sides by kⁿ.

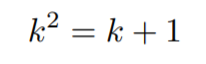
This quadratic is known as a characteristic equation, and is used in a variety of math topics like differential equations. This equation can finally be solved using the quadratic formula and we get:

Taking a Closer Look

The existence of two roots provides a valid reason for why there is no common ratio between the first few terms. So, we end up with the equation:

Where A and B are constants.

If we plug in two different values of n = 0 and n =1, and solve for A and B, we get:

Voila! We have finally arrived at Binet’s Equation for Fibonacci numbers.

Gut Check

Let us split this equation into multiple parts.

G(n) is the main driving force behind the equation. E(n) cleans up G(n) and provides an integer output. Let us take a look at some examples:

Let us plug in some value to see how this equation works.

From this we can see that G(n) provides an approximate value within 1 of the actual answer, and E(n) acts like a nearest integer function, which gets rid of the fractional part of G(n).

If I was to sum up Binet’s Formula, I would describe it as the taming of an everlasting recursion.

I will be writing more about how this relates to the golden ratio and more neat formulas related to the Fibonacci sequence. For now, goodbye.

Update:

I have written two more articles regarding the Fibonacci sequence, check them out if you want:

How Fibonacci Can Help Convert Miles and Kilometers

Why does 1/89 represent the Fibonacci Sequence