Public-key cryptosystems like RSA have become indispensable in the digital age. From helping to secure e-commerce, to ensuring private communication on messaging apps, they constitute critical internet infrastructure.

RSA’s power relies on the difficulty of factoring large integers. Other public-key cryptosystems depend on related challenges, like the discrete logarithm problem in the case of the Diffie-Hellman key exchange, to ensure their security. Despite their seeming impenetrability, RSA and many of its fellow public-key cryptosystems are facing a looming threat: quantum computers.

In the 1990’s, mathematician Peter Shor developed what is now known as Shor’s algorithm. Shor’s algorithm is designed to run on quantum computers, and is capable of factoring integers much more efficiently than any known algorithm that runs on classical computers. It can also be used to break cryptosystems that rely on the discrete logarithm problem (for those familiar with abstract algebra, this is because both integer factorization and the discrete logarithm problem are special cases of the hidden subgroup problem for abelian groups).

Significant efforts to build a quantum computer that can successfully and consistently run Shor’s algorithm on large integers are being made by researchers around the world. Although we currently have quantum computers consisting of 50–100 qubits, their quantum gates are still plagued by noise. These noisy intermediate-scale quantum computers (NISQ), do have some uses, but it will likely be many years until we have fully fault-tolerant quantum technology. A few skeptics even believe that it is impossible to build a fully fault-tolerant quantum computer at all.

So depending on when (or whether) a fully fault-tolerant quantum computer is built, the development of new classical algorithms for integer factorization could have a significant impact on the world of cryptography. We will thus survey some of the important existing classical factorization algorithms, and then examine how they might be improved to match the potential of Shor’s algorithm.

Factoring with Fermat

The first algorithm we discuss, Fermat’s factorization algorithm, is not used to factor the sorts of numbers the RSA cryptosystem relies on, but it does provide a basis on which we can construct more complicated methods that we can use to factor RSA numbers. Named after French mathematician and lawyer Pierre de Fermat, Fermat’s algorithm depends on the fact that we can represent odd numbers as the difference of two squares, i.e. N=a²-b²=(a+b)(a-b), where N, a, and b are integers and N is odd. This equality is true for all odd integers since if Ncan be factored as N=xy for two integers x and y, then

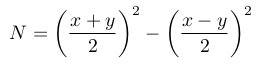
where x and y must be odd because N is odd.

The algorithm involves first computing ⌈√N⌉, and then plugging this value into a in the equation a²-N=b². If b² is a perfect square then we are done. If not, then we add one to the value we plugged into a and check if b² is a perfect square again. We continue this process until we find integer values of a and b that satisfy our equation, and then use those values to find the factors of N (since N=(a+b)(a-b)).

This algorithm is thus quite simple and is often not that useful. In fact, it is in many cases less efficient at factoring than naive trial division. But as we will see, we can use Fermat’s approach to develop much more powerful methods.

The Quadratic Sieve

Invented in 1981 by mathematician Carl Pomerance, the quadratic sieve is currently the fastest algorithm for factoring most integers with fewer than 100 decimal digits. Although the RSA numbers used in practice are almost always more than 100 decimal digits long, understanding the quadratic sieve is an important step on our journey to learning about even stronger algorithms.

Let’s now walk through the quadratic sieve algorithm. As we discuss each step, we will also demonstrate it with an example.

The first step in the algorithm is to choose a smoothness bound. We call a number B-smooth if all of its prime factors are less than or equal to B. The prime-counting function π(x) is relevant to the task of choosing a smoothness bound B, since it gives the number of primes less than or equal to the real number x.

In Fermat’s algorithm we plugged ⌈√N⌉ into the variable a in the equation a²-N=b², and then checked if b² was a perfect square. We modify this approach for the quadratic sieve algorithm by trying to find two integers a and b(a) where b is a function of a, such that all of the prime factors of the least absolute remainder of b≡(⌈√N⌉+a)² (mod N) are less than or equal to B. The set of prime factors is known as the factor base. The value of b(a) is thus B-smooth. When b(a) is B-smooth, the pair {⌈√N⌉+a, b(a)} is known as a relation.

The second step in the quadratic sieve algorithm is to plug small integer values into a in the equation

Since b(a) will start off relatively small, it has a decent chance of being B-smooth, as is required.

The number we will factor as our example will be 217621. This number is smaller than the integers the quadratic sieve would usually be used to factor in real applications, but it is convenient for the purpose of demonstration. Thus

We use Euler’s Criterion to find primes such that 217621 is a quadratic residue, or congruent to a square, modulo these primes. These primes make up our factor base, which we haven chosen to contain 13 primes: 2, 3, 5, 13, 17, 23, 29, 31, 43, 59, 61, 71, 73. It is possible we could need to expand this base at some point if it is difficult to find relations.

We choose to pass 3500 values through our sieve. In order to do this, we take values of a, contained in the matrix A, from 0 to 3499 and plug them into the function b(a), to get the values contained in the matrix B below.

We now execute the sieve for which the algorithm is named. First, we need to solve the equation b(a) = (467+a)²-217621 ≡ 0 (mod p) for each prime p in our factor base.

We used the Tonelli-Shanks algorithm to find the square roots modulo each prime.

The values of a modulo p that we found tell us which values of b(a) we can divide by p. For example, for p=5 starting with a=4 and then for every fifth value of aafter that, b(a) is divisible by 5 (b(a) is also divisible by 5 starting at a=2 and for every fifth value after that). Thus we divide all b(a) by the primes from our factor base by which they are divisible. We then look for the smooth values of b(a) whose locations in B now contain ones. In our example, the following values in Acorrespond to values in B that have been fully factored: [1, 41, 123, 327, 377, 617, 721, 1871, 2973, 3173]. Below are the smooth values in B and their factorizations.

1403=23*61
40443=3*13*17*61
130479=3*23*31*61
412815=3*5*13*29*73
494715=3*5*13*43*59
957435=3*5*29*31*71
1193723=17*23*43*71
5248623=3*23*29*43*61
11615979=3*29*31*59*73
13031979=3*17*59*61*71

We are looking for a product of some subset of these values which is equal to a perfect square congruent to (⌈√N⌉+a)² (mod N). We can find this product by creating a matrix where each row contains the exponent of a smooth number modulo two. We then solve for the left nullspace L in the equation below to get a number whose factorization contains only even exponents, and is thus a square.

So the subset of equations we use to get a square is the following:

40443=3*13*17*61
130479=3*23*31*61
494715=3*5*13*43*59
957435=3*5*29*31*71
5248623=3*23*29*43*61 
13031979=3*17*59*61*71.

The product of these values gives us b².

b²=40443*130479*494715*957435*5248623*13031979
b²=3⁶*61⁴*(5*13*17*23*29*31*43*59*71)²
b²=27²*3721²*4115557006795²
b²=413477665801673265²

We now find s²=(467+a)² by computing the product of each (467+a)² corresponding to the values used to compute b² above.

(508*590*844*1084*2338*3640)²=2333637221852518400²

So we can write the number we want to factor as the difference of two squares, as we did in Fermat’s Factorization method earlier.

s² - b² ≡ 0 (mod N)

2333637221852518400² - 413477665801673265² ≡ 0 (mod 217621)

Finally we can factor the difference of squares and find the greatest common divisor of one of these factors and N. This will either give us a trivial factorization of N (i.e. N=1*N), in which case we should try a different combination of values from B, or we will get a nontrivial factorization of N and we will be finished.

GCD((2333637221852518400 - 413477665801673265), 217621)=269

Therefore 217621=269*809, and we are done. Now we are ready to explore an even stronger algorithm than the quadratic sieve: the general number field sieve.

The General Number Field Sieve

The most powerful classical integer factorization algorithm we have today is known as the general number field sieve (GNFS). It’s cousin, the special number field sieve, was introduced by the British mathematician John Pollard in 1988, and was expanded to the GNFS by multiple researchers in the following years. The GNFS is usually the fastest algorithm for factoring numbers with greater than 100 decimal digits, and as of the writing of this article, the largest number it has factored is RSA-250, an integer with 250 decimal digits.

The superior performance of the GNFS is mainly due to its ability to find smooth numbers more efficiently than other methods. The GNFS finds smooth numbers that are subexponential in the size of N, whereas algorithms like the quadratic sieve find smooth numbers that are exponential in the size of N.

The key to finding these smaller smooth numbers relies on algebraic number fields. An algebraic number field is a finite extension of the field of rational numbers. To better understand this definition, let’s first define an algebraic number. An algebraic number is a complex number that is the root of a nonzero polynomial equation in one variable, where the coefficients are rational numbers. If an algebraic number is the root of nonzero polynomials only of degree n or higher, then it is called an algebraic number of degree n.

An algebraic number field can thus be described as all of the complex numbers produced by plugging algebraic numbers of degree n, into a nonzero polynomial in one variable and of degree n. So if α is an algebraic number of degree n, then polynomials of the following form give us an algebraic number field generated by α:

An algebraic number field is both a field and a vector space. Since the algebraic numbers α that we plug into the above expression are roots of nonzero polynomials of degree n, and thus satisfy the equation

we can write any power of α greater than or equal to n in terms of a linear combination of powers of α less than or equal to n, (a power greater than n might arise if we multiply elements of the algebraic number field together).

Given this information about algebraic number fields, we can now construct the GNFS algorithm. The algorithm begins by choosing two polynomials with each meeting four requirements:

1. They have coefficients in ℤ.
2. They are irreducible (not factorable into smaller non-constant polynomials) over ℚ.
3. They share some root r when taken modulo N
4. They both have degrees that are small

Once we have chosen two polynomials p(x) and q(x), of degrees a and brespectively, we attempt to find pairs of integers c and d such that the integers uand v below are both smooth relative to a factor base that we choose.

The usual approach to finding satisfactory c and d is to use a technique called lattice sieving. The original lattice sieving technique as developed by Pollard can be found here, and a faster version due to Franke and Kleinjung can be found here.

We then proceed to look for products of u and v such that they are simultaneously squares (this should remind you of the process we used in the quadratic sieve to find squares congruent modulo N). In most real-world applications where robust parallel computing resources are available, the algorithm used to find the nullspace is Thomé’s version of the Block Wiedemann algorithm, rather than Gaussian elimination.

Our products of u and v cannot just be squares though. We are working in a number field where they must also be field norms of squares. For the rings ℤ[y] and ℤ[z], where y and z are roots of p(x) and q(x) respectively, we have that u and v are field norms of c-yd and c-zd. Thus the products of u and v that are squares are also field norms of the products of c-yd and c-zd.

We now construct a difference of squares (as we did in the previous two methods) which will hopefully yield a nontrivial factorization of N. Both y and zcan be mapped to r by homomorphisms from ℤ[y] and ℤ[z] to ℤ/Nℤ. These maps give us integer representations in ℤ/Nℤ of the product of all the factors of the form c-rd (mod N) and their square roots (it is unlikely that the square roots of the products of u and v in the rings ℤ[y] and ℤ[z] will be rational, let alone integers). Thus our homomorphisms from ℤ[y] and ℤ[z] to ℤ/Nℤ give us integers s and t such that s²-t²≡ 0 (mod N). As we did in the quadratic sieve, we can take the greatest common divisor of s-t and N to possibly produce a nontrivial factor of N, thus concluding the GNFS algorithm.

The most obvious path to a faster classical factorization algorithm lies in optimizing GNFS. The process of choosing polynomials for GNFS is likely the step most amenable to improvement. Kleinjung’s method for polynomial selection seems to be the best approach we know of at the present, but it could certainly give way to more effective techniques.

Another approach to achieving more powerful classical factorization methods would be to develop a distinct successor to the GNFS, much as the GNFS succeeded the quadratic sieve. The development of the GNFS relied on the contributions of many mathematicians over multiple years. It took inspiration from the algorithms that came before it, and an assist from the world of algebraic number fields to factor larger numbers than had been previously practical to tackle. A new algorithm, whether inspired by the GNFS or not, would likely require a significant leap in our understanding of the fundamentals of integer factorization. Beliefs in whether any such classical algorithm could compete with a future implementation of Shor’s Algorithm will likely determine the amount of effort the mathematical community invests in studying new classical approaches. Thus as quantum computing technology evolves in the coming years, we will see how new hardware influences the development of new theory.