Convert Numbers Between Numeral Systems Using Logarithms

What one would do to find the representation of a number written in one base to some another would probably be to take a look at the Euclidean algorithm: Dividing the number by a new base, writing down the integer part, then divide it again, and again, until it will not reach 0. The order formed from the remainders represents the same number but written in this new base.

As an example, the algorithm applied to:

looks like this:

By writing down the remainders, we get the same number but in the binary system, that is:

What is the problem?

Having so many successive 0s that cannot be skipped. The algorithm flows from start to end without any breaking points. That is where logarithms come in handy because they could wipe out these places from the calculation.

What is the solution?

As we all know, if the result and the base of some exponential function are well-known, then logarithms are used to find this exponent, to find the power.

We also know that each numeral system in modern mathematic is positional. The number 1027 written in the 10-base system means just that:

Now let us think about how we could write the same number but with logarithms. Looking at the formula above, we notice that the base is known, it is 10, and the result is also known, it is 1027. Thus:

By using the logarithms table or just with any calculator, we get that b is 3.0115704436. Of course, it means that if we would raise 10 to this power, we would get 1027 — that is clear. Yet, we could get the same number with a little different approach. The power could be divided into two parts: integer and decimal. We take the integer one, which is 3, and calculate 10 to this exponent. What do we get? We get 1000. This gives us information that digit at the position of 10³ will be non-zero, and, in fact, it will be equal to the integer part of the following fraction:

and the remainder,

we use in the next step in the same manner as 1027 was processed in this one:

Notice that we computed digits at 3rd and 1st positions. We did not calculate the one at 10² since there is only 0. It was omitted from the calculation.

The next step is:

There is nothing left: the algorithm ends.

Now, what converting is all about?

Simply instead of using 10 as the base, we want it to be something else: 2, 3, 4, or so. How could we do this? The solution comes from the properties of logarithms: its base could be changed without changing the result. But before getting into the how at once and risking losing the ground, we will go to it step by step.

We know what logarithms are, it has been talked already. Knowing what base and result are, we could compute the power. Well, are the following equations the same?

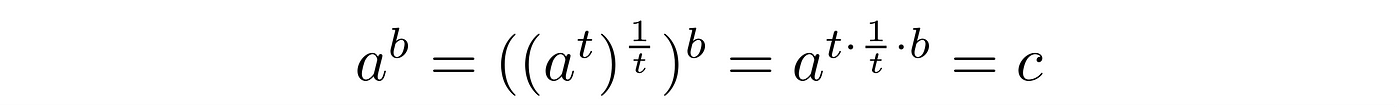
Yes. Though, the product of multiplication t times the fraction of 1 by t is 1. It does not change the exponent.

However, we do not want just to arise it like that. We want to use it for changing our base from a to a’. So we ask ourselves, “To what power do we have to raise a to get a’?” And what mathematic answers for such a question? Exactly, logarithms!

At this point, our equation looks like this:

There is no unknown left. We know what b is:

and what the fraction is:

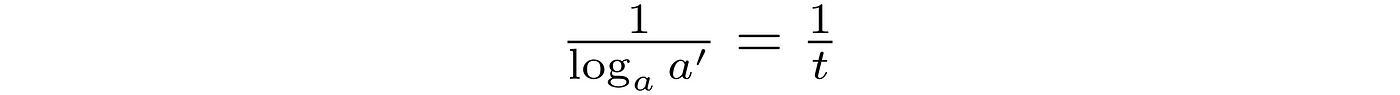
Then we could present the formula for calculating the same c but with another base. That is:

Examples

Let us convert our 1027 from the-10 base system into the binary one. We know how it looks by now, so it would be easier to follow. Where do we start? We need to calculate t to get a’, which is 2 (binary system.)

We could find the fraction immediately knowing what t is:

We know all the constants, thus the algorithm could be started.

First iteration:

Undoubtedly, we are working with the binary system, so any integer part will be 1, always. But we are going to calculate everything each time for getting better feelings.

Second iteration:

Look at how all 0s disappeared; it is so beautiful.

Third iteration:

Thus we know everything: 1s are at 10th, 1st, and 0th positions. All others have 0s. Let’s check this in the same way as we checked it after applying the Euclidean algorithm. Using the same table:

Maybe one more with some huge number, say 94842243, that we would like to convert into the 3-base numeral system let us go. Again, we start by computing tto get a’.

and the fraction:

Now iterations, and there are a few. When we break through calculations, we will check if the result is right. So, thus they are:

And a verification test,

gives the identical number.