Calculus and the Legend of the Founding of Carthage

The ancient Romans had a story about the foundation of the ancient city of Carthage. According to Virgil’s epic poem the Aeneid, Dido, the queen of the Phoenician city of Tyre, was forced to flee with her life when her brother usurped the throne and murdered her husband, the king. She eventually arrived in Libya, where she bargained with the king of the local tribes to be given as much land as could be enclosed by the hide of an ox. This may sound like a bad deal, but Dido was clever: She cut the hide into very thin strips, tied them together into a rope, and looped it around a plot of land by the shoreline in such a way as to maximize the area of her claim. To this day, the problem of finding a curve with fixed endpoints and fixed length that encloses the maximum area between the curve and the line segment between the two endpoints is known as the Dido problem.

The Roman poet Virgil wrote the Aeneid some time between 29 BCE and 19 BCE, a little over a century after Zenodorus published a treatise thought to have been titled On Isoperimetric Figures, which sadly is now lost to history and its content is known only through references to the work by other authors in Antiquity. The most important proof said to have been contained in this treatise was the proof that the area of a circle exceeds the area of any regular polygon with the same perimeter. Since this proof only pertains to regular polygons, it is not a full solution to the Dido problem, but if Virgil was aware of this treatise then it would have motivated the correct conclusion. Although it would take another 1900 years for the full proof to appear, Virgil was correct that Dido should have chosen an arc of a circle as the boundary for her new city.

By the time Virgil wrote the Aeneid it was widely understood by the ancients that the solution to the isoperimetric problem is a circular arc, so why did a full proof not appear until the 19th century? The answer is that the proof requires the calculus of variations, the study of the optimization of functionals, which are objects like definite integrals that take functions and return numbers. (See my article on the impossibility of trisecting the angle for another ancient problem that remained unsolved until the 19th century.) This article will show how to use the calculus of variations to solve Dido’s problem.

Let the x-axis represent the shoreline and suppose that the curve intersects the x-axis at x=0 and x=a, for some fixed a. In general, the curve cannot be represented as a function of x because it will violate the vertical line test:

For the sake of simplicity, let’s ignore this and assume that we’ve chosen the length of the shoreline segment in advance to be long enough for us to assume that we don’t have to consider curves that will violate the vertical line test, so that we can represent the curve by a function y(x). If we don’t do this then the strategy of the solution will be the same, except instead of a single function y(x) we would have to parameterize the curve by r(t)=(x(t),y(t)) and then maximize the area integral for the two functions x(t) and y(t).

Now we can set up Dido’s problem as a constrained optimization problem. We seek to find y(x) such that A[y], the area under the curve of y(x), has maximum value. This area can be written as a definite integral:

We are also subject to the constraint that the length L[y] of the curve is fixed, and this length can also be represented by a definite integral:

This problem can be solved by the method of Lagrange undetermined multipliers. We can insert an undetermined constant λ into the problem and use this to replace the constrained optimization of A[y] with an unconstrained optimization of a new functional I[y]:

By analogy with the problem of optimizing ordinary functions, the functional I[y] will take a maximum or minimum value when infinitesimally small variations δy in the input function y do not change the value of I[y], that is, when δI=I[y+δy]-I[y]=0. The variation δy is also a function of x, and we assume that its derivative δy′ exists and is also very small, and that y+δy and y′+δy′ agree with yand y′ at x=0 and x=a, that is δy(0)=δy(a)=0 and δy′(0)=δy′(a)=0. Note that δI is not really a derivative because the variation δy is a function so there’s no such thing as a limit as δy goes to zero. The δ notation can be thought of as a shorthand for a process of introducing a parameter that changes y into y+δy and then differentiating the integral with respect to that parameter.

Now we expand δI:

This seems bad, but let’s keep pushing forward and expand (y′+δy′)²:

This approximation is valid because δy′ is infinitesimally small, so (δy′)² is negligible. When x is very small, the binomial approximation says that for any power a, (1+x)ᵃ≅1+ax. Therefore:

This further simplifies δI:

Now let’s do integration by parts on the second term in the integrand:

Since δy(0)=δy(a)=0, the first term on the right hand side vanishes and we can write δI as:

For this to be zero for any arbitrary choice of δy, the term in parentheses must be identically zero, and this gives us a differential equation for y(x):

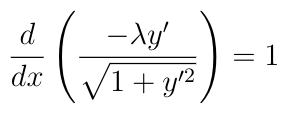
Now rearrange and solve the equation.

This equation describes a circle, and it is intuitively clear from the geometry of the problem that this should be a maximum of the area functional and not a minimum, so we have shown that the curve that solves Dido’s problem is a circular arc.

Conclusion

There are many interesting variations on the classic Dido problem that one can come up with. For example, if the ground is assumed to have varying altitude then we would have to optimize a three-dimensional curve instead of a plane curve, or if the goal was to maximize the integral of a position-dependent quantity like land value given that waterfront property is worth more than landlocked property, rather than just area. Dido-type problems are great for introducing calculus of variations because they all involve integrals of the following form:

The semicolon indicates that y and y′ depend on x, and f may or may not have an explicit dependence on x. In this integral, f is a function of y(x), y′(x), and x which takes y and y′ as input variables. Functionals of this type are extremely important in applied math, especially in physics where they motivate the Lagrangian formalism.

Set f equal to the integrand of I[y]:

Then observe that we can write δI as:

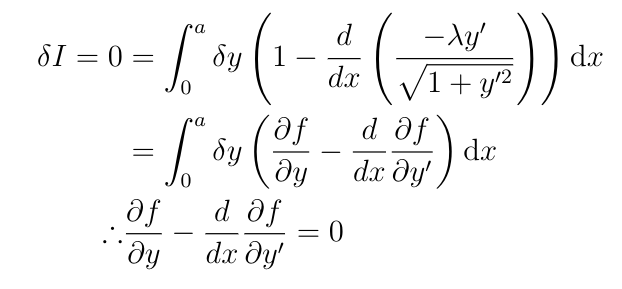
This is called the Euler-Lagrange equation, and it is one of the most important equations in both calculus of variations and advanced physics. Most introductory treatments derive the Euler-Lagrange equation first and then use it to solve the Dido problem, but I deliberately held off on deriving it here because the δ notation is very powerful and important to understand and because the Euler-Lagrange equation is so important that it deserves its own article, one which will be coming out in the near future.