The Mexican-born Israeli-American theoretical physicist J. Bekenstein was the first one to suggest that black holes, a region of spacetime where gravity is so strong that not even light can escape from it, should have a well-defined entropy. According to Bekenstein, one can define black-hole entropy as follows:

“Black hole entropy is the amount of entropy that must be assigned to a black hole in order for it to comply with the laws of thermodynamics as they are interpreted by observers external to that black hole. “

— Jacob Bekenstein

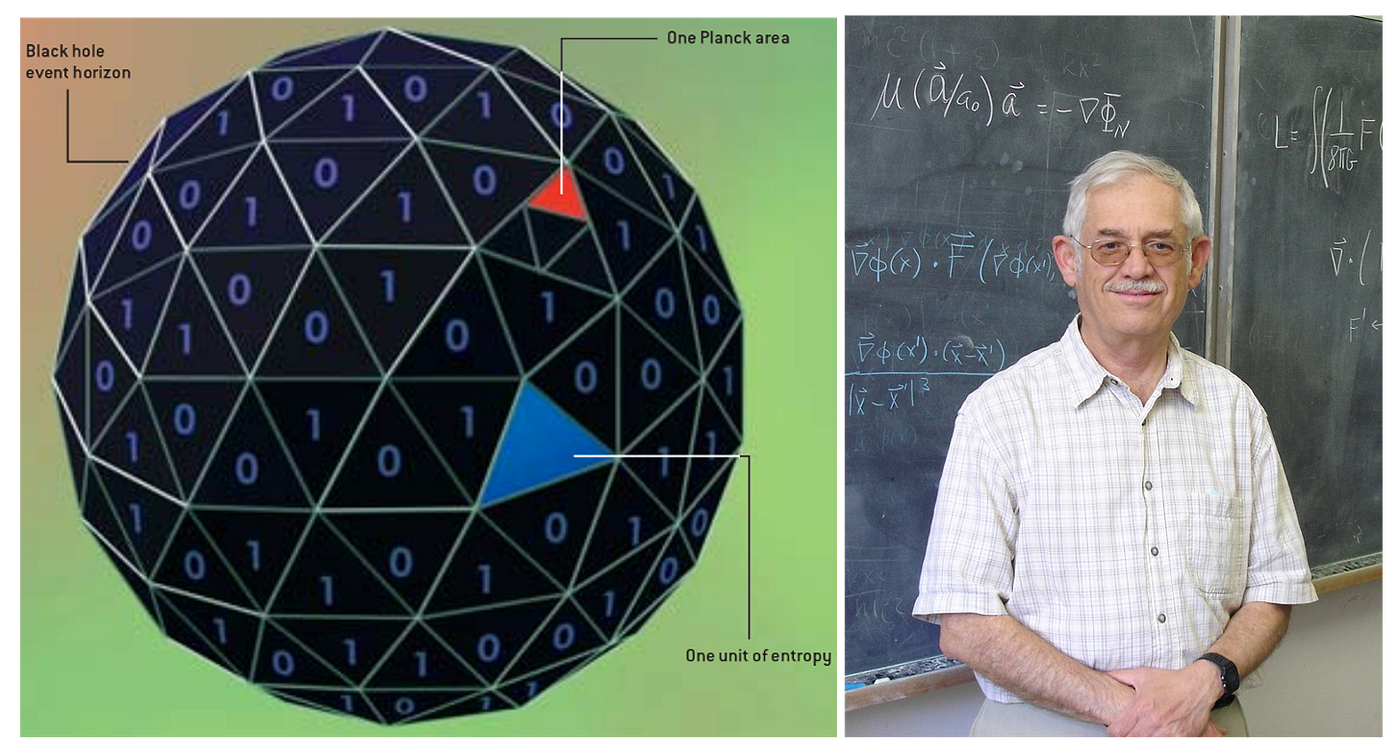
Why Black Holes Have Entropy?

In an article by Bekenstein, he provided three possible ways to justify the existence of black hole entropy:

• The matter and radiation that collapse to form a black hole are hidden to exterior observers. Hence, such observers cannot provide a thermodynamic description of the black hole’s collapse that is based on the entropy of the collapsed matter and radiation since those are not observable. A way to explain the thermodynamics would be to associate entropy to the black hole.

• Only three numbers are needed to parametrize a stationary (not to be confused with static) black hole: its mass M, charge Q, and angular momentum J (see the no-hair theorem). Since there are several possible formation scenarios for a black hole with a specific choice of these three parameters, there must be several possible internal states associated with it. We know that thermodynamic entropy quantifies the many microstates compatible with a given macrostate (characterized by quantities such as temperature T, pressure P, and volume V). In the case of the black hole, the macrostate is characterized by the tuple (M, Q, J). Quoting Bekenstein, “Thermodynamic entropy quantifies […] multiplicity. Thus by analogy, one needs to associate entropy with a black hole”.

• The black hole hides information. All information black holes provide are (M, Q, J), and it blocks all signals that enter it. Since we know from basic statistical mechanics that entropy measures missing information, this suggests that black holes have entropy.

The Black Hole Formula for the Entropy

It is reasonable to suppose that the entropy of a black hole should depend only on one or more of the three observable quantities, M, Q and J. According to the area theorem, the area of the event horizon of a black hole cannot decrease. This reminds us of the behavior of the ordinary thermodynamic entropy of closed systems. Therefore, it makes sense to suppose that the entropy of the black hole is a monotonic increasing function of the area of the event horizon.

Now, one can show (to be discussed later) that a black hole that obeys “a version” of the first law of thermodynamics possesses an entropy that is proportional to the area of the event horizon. More specifically, if the area of the event horizon is given by A, the black hole entropy is

where we used natural units (physical constants set to 1).

Types of Black Hole

There are four main types of black holes:

• Schwarzschild black holes which have mass M, charge Q=0 and angular momentum J=0.
• Kerr and Kerr-Newman black holes which have mass M, charge Q (the Kerrblack hole has Q=0, but the Kerr-Newman black hole is charged), and angular momentum J.
• Reissner–Nordström black holes which have mass M, charge Q, and angular momentum J=0.

In the following, I will briefly describe Schwarzschild black holes and Kerr-Newman black holes. The former is the simplest type of black hole and the latter is the most general. For a more detailed description see Carroll.

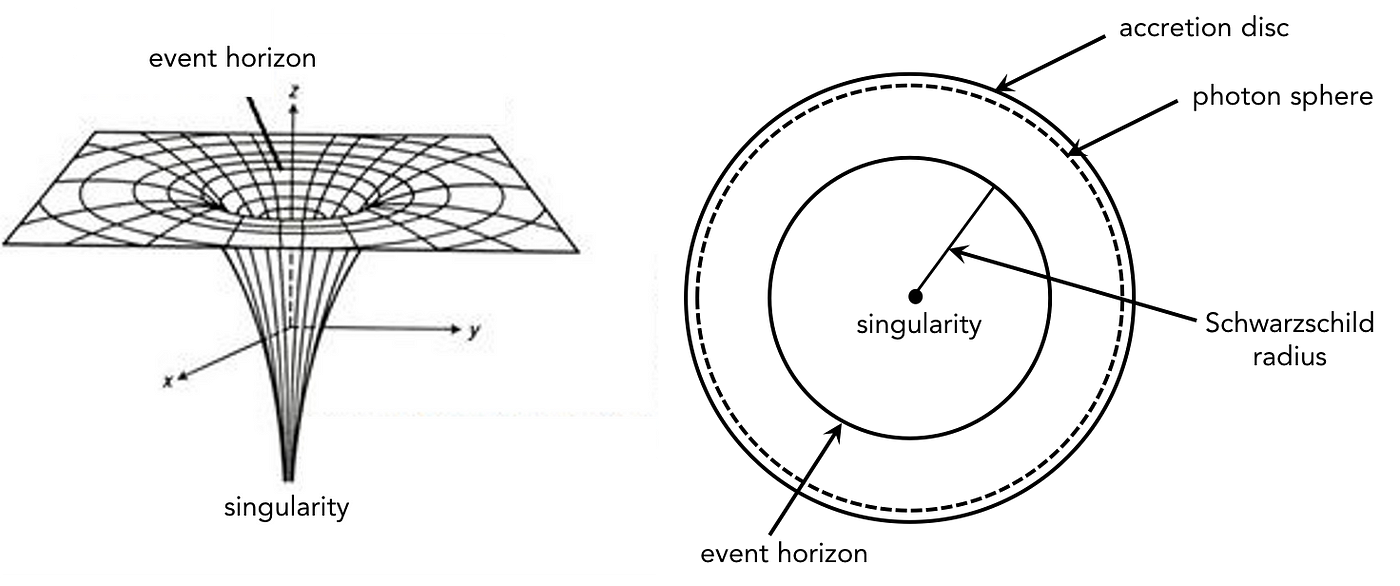
The Schwarzschild Black Hole

The Schwarzschild black hole is stationary and spherically symmetric with only one parameter, its mass M. The Schwarzschild line element in spherical coordinates reads:

Changing from spherical to a new set of coordinates called Eddington–Finkelstein coordinates, one finds that r = 2M is not a real spacetime singularity. The only singularity of the Schwarzschild black hole is at the center r=0. The radius of the event horizon is r = 2M and its surface area and corresponding entropy are given by:

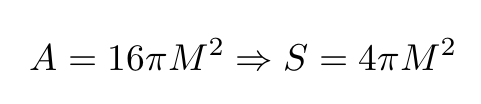
Kerr-Newman Black Hole

The Kerr-Newman black hole is the most general type of stationary asymptotically flat black hole. Note that stationary and static are different concepts. The Kerr-Newman black hole is spinning (hence it is not static) but it always spins in the same way, and is, therefore, stationary. The Kerr-Newman black hole has three parameters, namely, M, interpreted as the mass of the black hole (as seen by an observer at infinity), charge Q, and J, interpreted as its angular momentum (it is axisymmetric). It is a generalization of the Kerr black hole which has Q=0. In contrast to the Schwarzschild black hole, the horizon of the Kerr-Newman black hole is not spherical.

In the Boyer-Lindquist coordinates (t,r,θ,ϕ) the line element reads:

where:

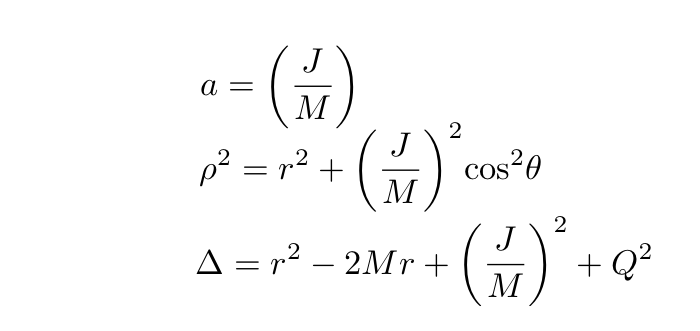
where θ is the polar angle in spherical coordinates. We also need to know the electromagnetic field tensor for the solution of the Einstein field equations to be obtained. In the Boyer-Lindquist form, the electromagnetic field tensor reads:

The equations of motion of a test particle with charge per mass q orbiting around the Kerr–Newman black hole are given by:

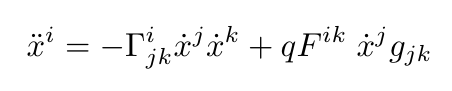
Note that the equation of motion depends on the Christoffel symbols Γ. The animation below illustrates the motion of the test particle.

The area of the event horizon of the Kerr-Newman black hole is given by:

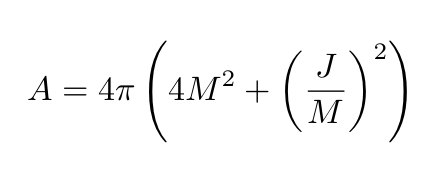
We note here that though the horizon of the Kerr–Newman black hole is not spherical anymore, in the Boyer-Lindquist coordinates it still lies at a fixed radial coordinate allowing Eq. 8 to be calculated in a simple way (see Bekenstein).

Important Surfaces of the Kerr–Newman Black Hole
As shown in Fig.8, the Kerr–Newman metric has the following important surfaces:

• The inner and outer event horizons:

• The inner and outer ergosphere:

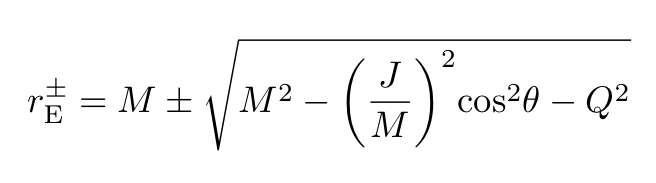
where θ is the polar angle in spherical coordinates.

The Laws of Black Hole Thermodynamics

I will first consider the first, second and third laws of black hole thermodynamics and then examine the zeroth law.

The First Law of Thermodynamics

When a thermodynamic system at temperature T is near its equilibrium and changes its state, the following relation holds between the corresponding increments of energy E and entropy S:

If the system is under rotation with angular frequency Ω and it is charged up to an electric potential Φ, its angular momentum and charge will vary. The first law Eq. 9 will then become:

Black holes admit a relation analogous to Eq. 12. To explain it I will consider only the Kerr-Newman black hole type since, as mentioned before, it is the most general (asymptotically flat) type of stationary black hole.

Now consider Eq. 8 for the area of the Kerr-Newman black hole horizon, calculate dA and multiply it by the parameter Θ below. We obtain the following relation between the dM, dJ and dQ:

where:

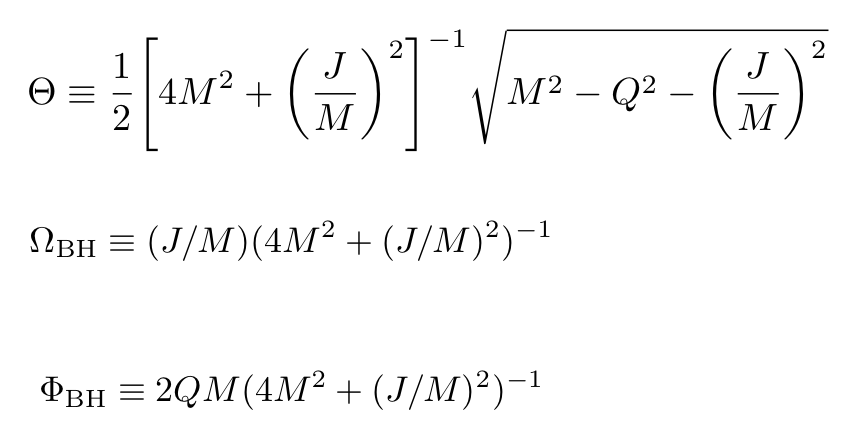
The quantities above:

are respectively:

• The angular rotation frequency of the black hole (any test body dropped into the black hole close to the horizon, ends up circumnavigating it at this frequency).
• The black hole’s electric potential (the line integral of the black hole’s electric field from ∞ to the horizon).

Since the first term of the right-hand side of Eq. 13 is the energy of the black hole, Eq. 13 is very similar to the first law of ordinary thermodynamics. For Eq. 13 to be the first law of black hole thermodynamics the entropy must be a univariate function of the area of the event horizon which would imply that:

Now, if we choose the entropy of the black hole to be Eq. 1, we find the following expression for the temperature of the black hole:

For Q=J=0 this becomes:

But in 1974, it was shown that a black hole spontaneously emits thermal radiation precisely with this temperature, the so-called Hawking temperature.

Though in Hawking’s original paper, Eq. 18 was obtained, the temperature in the presence of charge Q and angular momentum J was later shown to be equal to Eq. 17.

The Generalized Second Law of Black Hole Thermodynamics

According to standard thermodynamics, the second law demands that the entropy of a closed system must never decrease:

Since conventional systems that fall into a black hole become unobservable, so does their entropy. A more useful law is then obtained if one generalizes the second law of thermodynamics as follows:

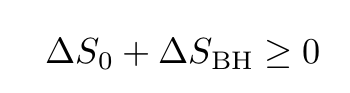
Hence, according to the generalized second law (GSL), the variation of the standard entropy S₀ outside the black hole summed with the variation of the total entropy of the black hole must never be negative. When the entropy of matter enters the black hole, the GSL demands that the increase in the entropy of the black hole must more than compensate for the decrease of the entropy from sight.

While the black hole is emitting radiation, there is a decrease in the black hole’s area, which violates the area theorem we discussed previously. Such violation happens because the energy condition assumed by the theorem fails due to the presence of the quantum fluctuations which themselves produce the radiation. The generalized second law predicts that the entropy of the outgoing radiation shall more than compensate for the black hole entropy drop.

The Third Law of Black Hole Thermodynamics

The third law of standard of thermodynamics can be stated in two ways:

• Unattainability statement: For a system to be taken to T=0 an infinite number of steps is needed.
• The Nernst-Simon statement: At T=0 the entropy of a system can either go to zero or become independent of the intensive thermodynamic properties such as pressure, magnetic field or the electric potential.

From our previous equations for the Kerr-Newman black hole, we find that if the black hole temperature given by Eq. 17 vanishes, two things can happen:

• The black hole Nernst-Simon third law statement. More specifically, at zero temperature the black hole entropy is not zero and, instead, depends on the ratio J/M, which is related to the black hole’s angular velocity, an intensive parameter.
• Second, there exists some indication that black holes satisfy the unattainability statement. As found by Thorne (1973), in an astrophysical scenario, the spinning process of an uncharged black hole gets delayed at J/M≈0.998M, before the vanishing of the extremality condition is satisfied.

The Zeroth Law of Thermodynamics

According to the zeroth law of thermodynamics, if two systems are in thermal equilibrium with a third system, then they are in thermal equilibrium with each other. Systems in thermal equilibrium have a constant temperature.

Since it can be shown that the surface gravity κ (which equals the acceleration due to gravity close to the horizon times the redshift factor) is constant on the horizon of a stationary black hole it is reasonable to associate it with the temperature T for a normal system.

What Is the Origin of the Black Hole Entropy?

This question still has no definite answer. However, since ordinary entropy is a measure of the multiplicity of microstates corresponding to a single macrostate, such as in Boltzmann formula

one is led to wonder what is the meaning of the black hole microstate. Here is a shortlist of some possible interpretations of black hole entropy (for more details see Bekenstein):

• The black hole entropy counts how many internal states of matter and energy there are (see this article).
• For a black hole formed by collapse, there is entanglement between the quantum field degrees of freedom external and internal to the horizon. For external observers, the degrees of freedom internal to the horizon are (naturally) not accessible. Hence, in a meaningful state, internal degrees of freedom are traced out.
• The black hole entropy counts horizon gravitational states. The microstates we are looking for are therefore the states of the gravitational degrees of freedom that reside on the horizon of the black hole.

My Github and personal website www.marcotavora.me have some other interesting material both about physics and other topics such as physics, data science, and mathematics. Check them out!