Beyond Infinity

In part one we introduced holomorphic and meromorphic functions along with their interesting properties. In this part, we shall continue down this road, but with a focus on yet another amazing fact about holomorphic functions.

Before stating these famous results let’s get a feeling for different representations of functions.

Let’s define the function g as the following

It is clear that |z| < 1 because otherwise the series diverges i.e. becomes infinite.

If we consider g as a complex function of a complex variable, its domain is the unit disk i.e. the disk centered at 0 in the complex plane with radius 1. This is called the radius of convergence of the power series.

That’s all fine but it turns out that we can represent this function in another way on this disk, namely

It can be easily proved that on the unit disk the two functions coincide. But clearly, they are not equal as functions because their domains differ. However, as we will soon see, there is a sense in which these two functions are merely two representations of the same function.

We will get back to this in a bit. For now, it will be beneficial to keep this example in the back of your mind as we proceed.

The first step towards this is an amazing fact of holomorphic functions.

The Identity Theorem

The identity theorem for holomorphic functions states the following:

Given two holomorphic functions f and g on a domain D, if f = g on some A ⊆ D where A has an accumulation point, then f = g on D.

This means that a holomorphic function is completely determined by its values on a single open neighborhood in D.

In layman’s terms, this says that if two holomorphic functions are equal on a disk (no matter how small) then they are equal everywhere.

Everywhere of course meaning “whenever it makes sense”.

So somehow the strict requirements that a function needs to pass in order for it to be holomorphic puts such structure on the function that all of its information is contained in its image of the smallest area imaginable. Local information is somehow also global information for holomorphic functions!

Analytic Continuation

Suppose f is a holomorphic function defined on a non-empty open subset U of the complex plane ℂ. If V is a larger open subset of ℂ containing U, and F is a holomorphic function defined on V such that

F(z)=f(z) for all z in U then F is called an analytic continuation of f.

Let’s again translate that in more understandable words:

If two holomorphic functions f and F are equal on some domain U and F is holomorphic on a larger domain containing U, then F is called an analytic continuation of f.

Now, here’s the kicker:

The identity theorem implies that analytic continuation is unique in the sense that if there was another holomorphic function G defined on V such that G(z)=f(z) for all z in U then F=G.

This is a remarkable result. It means that there is only one way of extending an analytic function (if the extension needs to be analytic as well, that is).

If we think about our example above with g being the geometric series from above and g* being the closed-form expression equal to g on the unit disk, we can now confidently say that g* is the unique holomorphic extension of g on the domain ℂ\{1}.

Mathematicians tend to think about an analytic continuation as the same function as the one it is extending but with different possible representations on smaller domains.

Applications of Analytic Continuation

This is all fine, but what can we use it for?

I think one of the best examples of how useful this is, is the work on the Riemann Zeta Function.

We start by defining the function as

Note that the real part of s needs to be greater than 1 since otherwise, the series would diverge.

It turns out that this function has another expression on the same domain in terms of a product over all the prime numbers called an Euler product.

This is an amazing piece of mathematics found by the great Leonhard Euler and what it is really saying is that there is some information about the prime numbers hidden in the zeta function.

The fact that the two expressions of the zeta function are equal means loosely that there is some bridge between the additive and multiplicative world. As it turns out, the real dictionary between them lies beyond the domain Re(s) > 1 and therefore we need analytic continuation.

In fact, the information we need from the zeta function in order to extract information about the distribution of the prime numbers turns out to be how a subset of its zeros are distributed. This subset is the set of zeros that lie in the so-called critical strip 0 < Re(s) < 1.

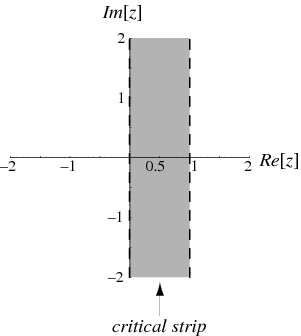
Note that a zero of a function f is a number r such that f(r) = 0.

Riemann conjectured that all these zeros lie symmetrically in the strip on the vertical line Re(s) = 1/2. This is called The Riemann Hypothesis and is one of the biggest unsolved mysteries in mathematics.

But back to the main topic. The information lies outside the region of convergence. Now, how do we analytically continue the Riemann zeta function?

There are several ways of doing this, actually. I will give you two quite interesting ways here.

The first way is to note that if we take the zeta function as defined by the infinite series above and then subtract the “even” terms two times, then we get the alternating zeta function, but this is also a product where the zeta function itself is a factor. That is

Rearranging and simplifying this equation a bit yields:

And since it can be shown that the eta function (i.e. alternating zeta function) converges for Re(s) > 0, this is in fact an analytic continuation of the Riemann zeta function.

Note that the set of zeros of the eta function includes all the zeros of the zeta function because of the product rule a ⋅ b = 0 ⇒ a = 0 v b = 0.

Another amazing way of analytically continue this function is through a functional equation first discovered by Riemann himself.

This is in my opinion one of the most beautiful relations in all of mathematics.

the second to last factor in the right-hand side above is called the gamma function and is a very well-studied function. It is a generalization of the factorial to complex numbers.

We clearly see that the zeta function must have zeros at the negative even integers because of the sine term that vanishes there.

This gives an analytic continuation to the whole complex plane except for s=1. Still, the functional equation is valid as an equation of meromorphic functions on all of ℂ.

Evaluating Infinite Quantities

This topic has been creating quite a stir in the mathematical community as some physicists have claimed that one can simply do some unjustified manipulations and set the infinite divergent series like 1 + 2 + 3 + 4 + … equal to -1/12 for example. This is of course nonsense (and they know it).

That being said, there are some spooky things going on in this direction that I don’t think we fully understand yet. Physicists call it zeta regularization, renormalization techniques, and other fancy names, but there are still some questions that we need to come to grips with that we haven’t explained.

Let me try to elaborate through an example.

It turns out that if you try to make a vacuum then no matter how good a job you do, particles (known as virtual particles) will pop in and out of existence all over the place all the time. We are now in the realm of quantum mechanics, so hold on to your hats and socks.

This phenomenon of virtual particles is called quantum fluctuations and it all has to do with fields. Not mathematical fields but quantum fields. A field is a property of space where each point has a value. For example, if we consider temperature to be continuous, then that would be like a field because then each point has a value associated with it namely its temperature, but as we all know, since the temperature has something to do with the kinetic energy of particles, it is not exactly continuous. However, in physics, we work with fields, such as the electromagnetic field or the gravitational field which are true fields.

The fields mentioned above are force fields but actually, particles of matter also have fields associated with them. The electron has the electron field, the up quark has the up quark fields, and so on. This is because all particles (in this theory) are really excitations in their underlying field so for example, the photon is an excitation in the electromagnetic field.

This theory is called Quantum Field Theory and it is very interesting from a mathematical point of view because of perturbation theories, path integrals, symmetry groups, and operators involved.

All fields — in particular electromagnetic fields — have fluctuations. In other words, at any given moment their actual value varies around a constant, mean value. Even a perfect vacuum at absolute zero has fluctuating fields known as “vacuum fluctuations”.

If we trap the particles between two non-charged, conductive metal plates then as we cut the space into parts, we put a restriction on the particles that would appear in between the plates. As a consequence, there will be emitted a force on the plates because there would be lower total energy between the plates than outside them, and in order to calculate the total force emitted from these energies, we end up with an expression in which one of the factors is the infinite divergent series

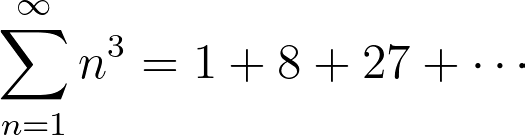
This looks like someone has tried to evaluate ζ(-3) by using the infinite series definition which was only allowed for Re(s) > 1, remember?

Where does this come from? It seems their calculation blows up when trying to evaluate this. Well, in a high-level view, what is happening is that when two metal plates come very close (a few nanometers) to each other, then the number of possible virtual particles that can pop in and out of existence between the plates is limited by their wavelength since it cannot exceed that of the distance between the plates. However, on the outside, the particles don’t have this limitation, and a lot more possibilities occur. This creates a force from pure quantum mechanical properties of space on the plates, pushing them against each other.

This phenomenon is known as the Casimir effect.

In the theoretical calculation of this energy that leads to an attractive force, we end up having to sum over all possible energies of these standing waves or modes (the particle’s energies if you wish). Depending on the dimension, we get a divergent series of the same type as above because all the standing wave’s wavelength can be written as multiples of the same constant and in our case n³ for each natural number n. The constant multiplied by the terms n³ has itself both Planck’s constant and π as factors but that is not critically important to understand for this article to be meaningful.

This energy seems to be infinite in these calculations, but of course, physicists knew that it wasn’t. If you take a look at the series above and you have to give it a finite value, then a good guess would be the analytically continued Riemann zeta function evaluated at -3.

After all, if you put -3 into the series definition of the Riemann zeta function, then you get the infinite series that we need to “evaluate”.

Let’s use the functional equation to evaluate ζ(-3). We need to calculate the following:

• We know from Euler that ζ(4) = π⁴/90
• Of course, 1/2³ = 1/8
• Γ(4) = 3! = 6
• sin(-3π/2) = 1

When we plug the above in the formula, we get

ζ(-3) = 6 ⋅ π⁴/ 8⋅90⋅ π⁴ = 1 /120.

Note! This is not the value of the above series. This is the value of the (analytically continued) Riemann zeta function at the point -3. The series (of all the natural cubes) diverges and the series expression of zeta is not defined at -3.

But the amazing thing is that when physicists substitute the infinite beast with the number 1/120 in their formula, then lo and behold, when they actually do the experiment in the lab, they measure the exact amount of force that was predicted by analytic continuation! It works!

What is going on here? Did nature just swallow an infinite chunk of energy for free?

Well, waves and energies can annihilate other waves and energies and it just so turns out that when all the dummy energies have been canceled, then the true regularized value remains.

But it is still interesting that it seems like nature really agrees with the value we get from analytic continuation. Because make no mistake, this is a natural phenomenon — a quantum property of space stemming from the true nature of particles and fields.

The following is a quote from one of my favorite mathematicians commenting on this kind of calculation.

It is like surgically removing an infinite value that covers the true value. Like a piece of gold inside an infinite amount of dirt. And I am suprised that every time we encounter such a series in mathematics or in physics, we get the right result by replacing it by precisely its finite regularised value. In physics these kinds of calculations are done all the time. This is properly the best kept secret in quantum physics.

~ Edward Frenkel