Becoming a master at physics requires a lot of work, but learning the techniques and guidelines in this article is taking the first step.

People often talk about physics as if it were merely a set of facts and equations: F=ma, energy can neither be created nor destroyed, E = mc², stars are giant balls of hydrogen fusing into helium and heavier elements, etc. These facts and equations can either form the base of our understanding or result from our understanding, but to do physics is to connect the two. In other words, learning physics requires learning techniques and guidelines alongside facts and equations.

I won’t be able to go through every single technique and guideline used in every single problem, but I do want to cover some of the most common techniques and guidelines used in physics.

Use an Explicit Equation if You Can

Except in the specific case where you are asked to derive an equation, you can use the given equations to solve a decent number of problems using some plug and chug and basic algebra. As long as you know all but one value in the equation, you can get that one value.

Example: Celestial Mechanics

How long would it take Earth to go around the sun if the mass of the sun were one one-hundredth of what it currently is and Earth’s orbit was unchanged?

Kepler’s third law relates the mass of the sun, the radius/semi-major axis of the orbit, and the period of the orbit, so we can get the period by solving Kepler’s third law for T and plugging in the values we already know.

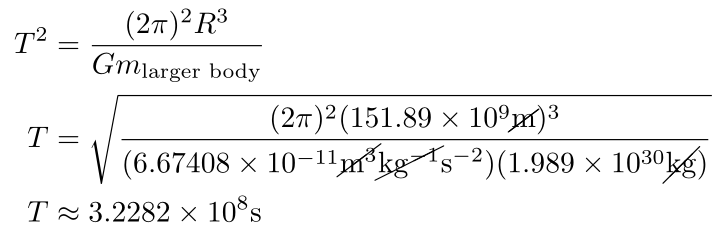
An Advanced Trick

Whenever you have a physics problem that changes a few values (in this case, the mass of the sun) in a formula, try to express your answer in terms of the values before the change. For this problem, we don’t have to look up any of these physical constants in the problem and we don’t even need a calculator.

Note that the blue-green expressions are the same, so we can substitute it back in without having to know anything except that the Earth takes a year to go around the sun. You could get a similar result by dividing the period for the earth by the new period and canceling out terms.

Extension of This Principle

I’ve only discussed the case where you have a singular equation with one unknown, but if you have n equations, you can have n unknown values. We’ll go through specific examples later.

Move Forward on Any Front, No Matter How Small

If you ever find yourself in a situation where you don’t know how to get from the information given in the problem to what the problem asks of you, take the information you have and do something with it, even if you don’t know how it could help you. Physics often requires you to take what you know, find an equation that can get you some more information, and then repeat the process until you have enough information to answer the question. When following this technique, remember to look at all the information you have even if you’ve used it before.

Example: Kinematics

How long does a runway need to be for an airplane with mass m moving with a constant net force F to reach a velocity vf from rest?

The phrase “How long does a runway need to be” means you’re looking for a distance. You know the mass, the force, the initial velocity (0 m/s since you’re at rest), and the final velocity. Because you’re trying to use an explicit equation if possible, you look for any equation on your equation sheet, but you don’t find any. Remembering that you’re trying to get whatever information you can, you instead look for equations where you know all but one variable. You’ll find the classic F = ma, and realize that you know F and m, so now you have a, the acceleration. Now, you look for equations where you know all but one variable, and you find that one of the kinematic equations has a, s(distance/displacement), vi (initial velocity), and vf (final velocity):

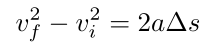
Realizing you know everything except for the distance, you can solve for the distance and answer the problem.

With More Experience

As you get more experienced, you’ll remember patterns like “using F = ma and then using a kinematic equation to get velocity, time, or distance” and you won’t have to look through all the equations on the equation sheet to find the relevant equation. With all the time you’ve saved, you can work on other problems.

I’ll give you methods that work in the examples for later sections, but I only figured them out because I kept following this guideline, making mistakes, and learning from them. There are only so many ways to make a mistake solving a problem. So long as you keep trying and you try to not make mistakes you’ve already made, you’ll run out of mistakes to make.

Look at Each Dimension Individually

In Cartesian coordinates (i.e. the standard (x, y, z) coordinate system) each dimension is orthogonal, meaning you can look at each dimension individually. In practical terms, you can create a system of equations with one equation per dimension. You can use this technique on any quantity that can be expressed as a vector, including velocity, momentum, forces, angular momentum, and torque.

Extensions of this Technique

In higher level physics, you’ll see a few other extensions of this technique: the use of symmetry to reduce the number of equations you have to consider, the separation of variables technique, and the eigenfunction expansion technique (you can treat each eigenfunction as if it were a separate dimension). Since I don’t want to duplicate work and the separation of variables technique leads directly into an eigenfunction expansion, I’ll only do an example of the symmetry technique.

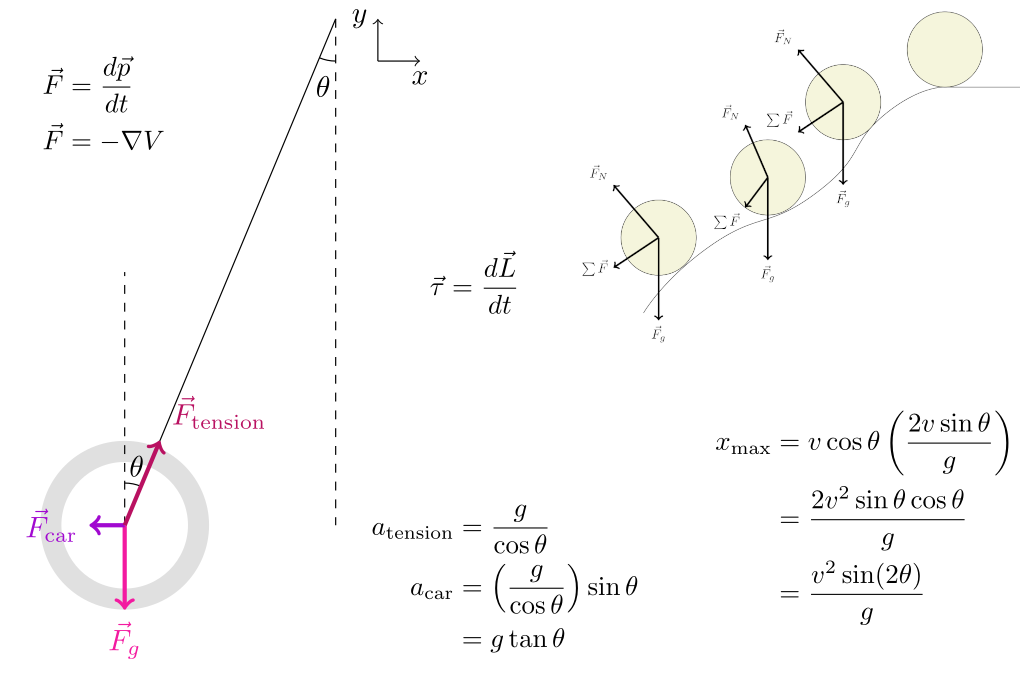
Example: Ballistics

Ignoring air resistance and assuming the curvature of the Earth is negligible, what is the maximum ground range of a cannon with muzzle velocity v?

We can consider the x and y dimensions individually and use kinematic equations to solve for an answer. We’ll have to split the velocity into its x and y components using sine and cosine. Note that since we have a system of two equations, we can have two unknowns, as I said earlier in the Explicit Equation section. Unfortunately, we seem to have three unknowns since we don’t know θ, the angle the cannon is fired at, but we can get another equation since we’re trying to maximize the range. We’ll get the range in terms of a single unknown, then we’ll take the derivative of the range with respect to that unknown, set it to zero, solve for the unknown in the new equation, and then pick the solution that gets us the maximum value.

In this case, we know

• the initial position: (0, 0)
• the initial velocity vector (in terms of other variables): (v cos θ, v sin θ)
• the acceleration vector (gravity pulling it down): (0, -g)

We also know the final y position since the range refers to how far it goes before it hits the ground, which happens when y is zero again.

Two kinematic equations relate initial velocity an initial acceleration to a position, and each has a different unknown. If we use the one that has the final velocity as an unknown (the one we used earlier), we end up with

in the x direction and

in the y direction, where we took the negative solution since the cannonball is moving down when it hits the ground. This kinematic equation didn’t get us a distance because we couldn’t use information from one equation to solve the other and vice versa. If we instead use the kinematic equation that has time as an unknown

we end up with

which means we can get an answer by solving for t in terms of θ or vice versa. Looking at the y equation yields

where we chose the nonzero solution of t since the cannonball is at (0, 0) at t = 0. Since we have t in terms of θ, we can plug it back into the equation for the range, which gets us

Now, the only unknown is θ, so we want to find the angle that maximizes the distance fired, which we do by using the process described earlier in this section (or use the fact that the max of sin θ is 1 and skip this part).

You can solve this equation in multiple ways, but I’m going to do it the pure math way (which will become more useful in later math and physics though it’s overkill for this problem). I’m also going to use radians because math and physics are generally easier with radians.

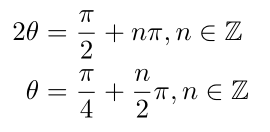
The first equation comes from the fact that cos(θ) has a zero at 1/2 π (90 degrees) and repeats every integer multiple of π (180 degrees), which is what the right-hand side of the first equation means (1/2 π plus some integer multiple of π). From there, I divide both sides by 2 and end up with the possible values of θ. Since θ has to be in the range 0 (firing straight forward) to 1/2 π (firing straight up), the only θ that maximizes the distance the cannonball travels is 1/4 π (45 degrees).

Plugging everything in gets us the final answer:

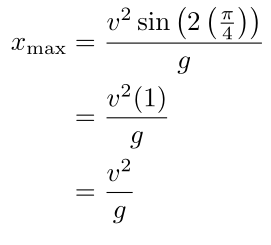
Example: Balanced Forces

A car moves forward with a constant acceleration. Inside that car, a ring of mass m at equilibrium hangs from a taut string at an angle θ difference from hanging straight down, as shown in the diagram. Determine the acceleration of the car.

There are three forces on the ring:

• acceleration of the car
• gravity
• tension from the string

Since we’re dealing with forces on an object with a known net acceleration (i.e. 0 since it’s in equilibrium) and we know the directions of all the forces, we can draw a free body diagram.

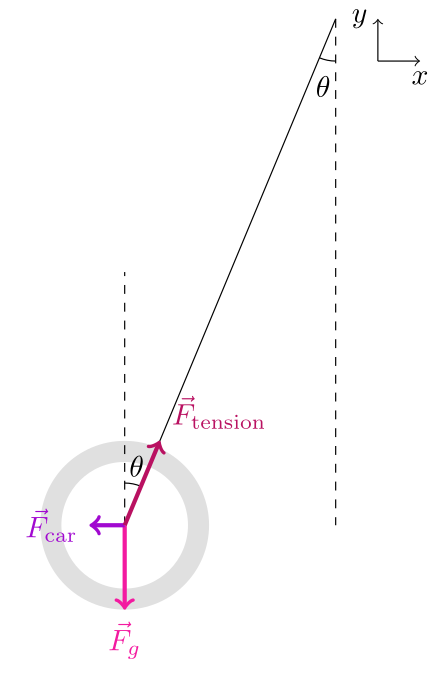
Note that the force from the car is entirely in the x direction, the force from gravity is entirely in the y direction, and the force from tension has both x and ycomponents. As in the previous problem, we can break the tension force into its x and y components using sine and cosine. Note that since θ is relative to the positive y axis, we get the y component of the tension by multiplying by cos(θ), not sin(θ). Likewise, we have to multiply by sin(θ), to get the x component of the tension. By breaking this system into one equation per dimension, we end up with

You might be thinking that we’re stuck because we don’t know any of the forces right now besides gravity (it’s -mg). We can try a few things, but we can make the substitution F = ma, for all the forces, and since all forces are affecting the ring, we can do the following

After that, we solve for the acceleration of the car and end up with an expression in terms of the acceleration from the tension and θ.

We know θ, so we need another equation that relates the acceleration from the tension to something else we know. In this case, it’s θ and g. Plugging the expression for the acceleration from the back into the acceleration from the car gets us our final answer of g tan(θ) through the process below.

Notice that you didn’t need to use the mass of the ring even though it was given in the problem. In the real world, you’ll often have more information than you need, so you’ll need to figure out which information to use and which to ignore.

A Shortcut

Since the forces add up to zero, if you put the vectors end to end, they make a triangle with the tension force as the hypotenuse, the car force as the opposite side, and the force of gravity as the adjacent side, which means you can use the definition of tangent to get the answer. This shortcut is kind of rare to use, but it works here. If you’re confused about how to use this shortcut, don’t and use the procedure above.

Example: Symmetry in Electric Fields

What is the electric field a distance r away from an infinitely long line of charge (i.e. a wire) with uniform charge density λ and no current?

This problem will come up later in your study of physics and requires vector calculus to fully understand, but the general principle of symmetry still stands.

If you wanted, you could integrate over the entire wire and get an answer, but Gauss’s Law requires less work (I can look at this problem and tell you the answer is λ/(2πεr) because the math is pretty easy with Gauss’s Law, but I’m going to go through the entire process so you understand what’s happening behind the scenes). To use Gauss’s Law as efficiently as possible, however, we have to find a complete set of surfaces that we can use anywhere on the wire such that the electric field doesn’t vary in magnitude or direction relative to the surface. You might be thinking that we’d already have to know the electric field to find such a surface, but we can use the symmetry of the problem to figure out the surface. I’m going to set my coordinate system so the line of charge goes in the zdirection, which you can imagine going up and down. I’m also going to assume the charge is positive in all the diagrams (meaning the electric field points away), but if λ is negative, switch the direction of all the arrows in the diagram.

Since the line of charge is infinitely long, it shouldn’t matter what section of the wire we look at. Each point on the wire will have the same amount of charge the same distance away on either side.

This fact gives us two simplifications we can make:

• The wire has translational symmetry along its length, meaning the zcomponent of the wire doesn’t matter and we can select any section of the wire to draw our surface.

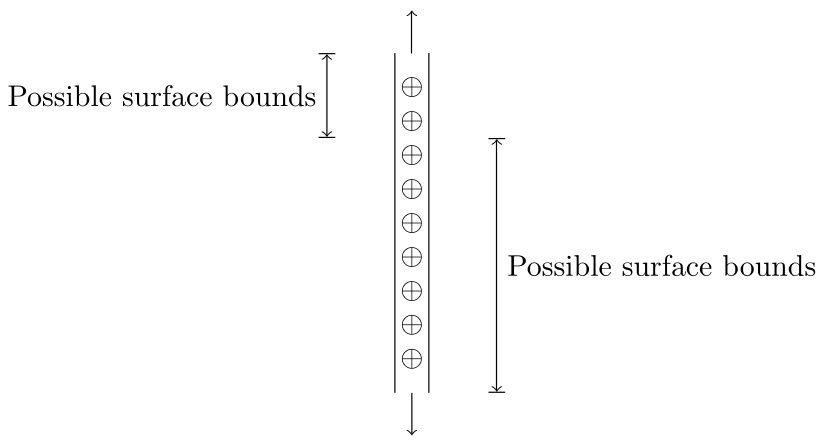
• The electric field has a zero z component since the charge distribution is symmetric in the z direction around each point.

We can also notice that rotating around the line of charge doesn’t change the distribution of charge, so we also have rotational symmetry, meaning the electric field can’t look like

where the red dot is the wire coming out of the screen. It also can’t look like

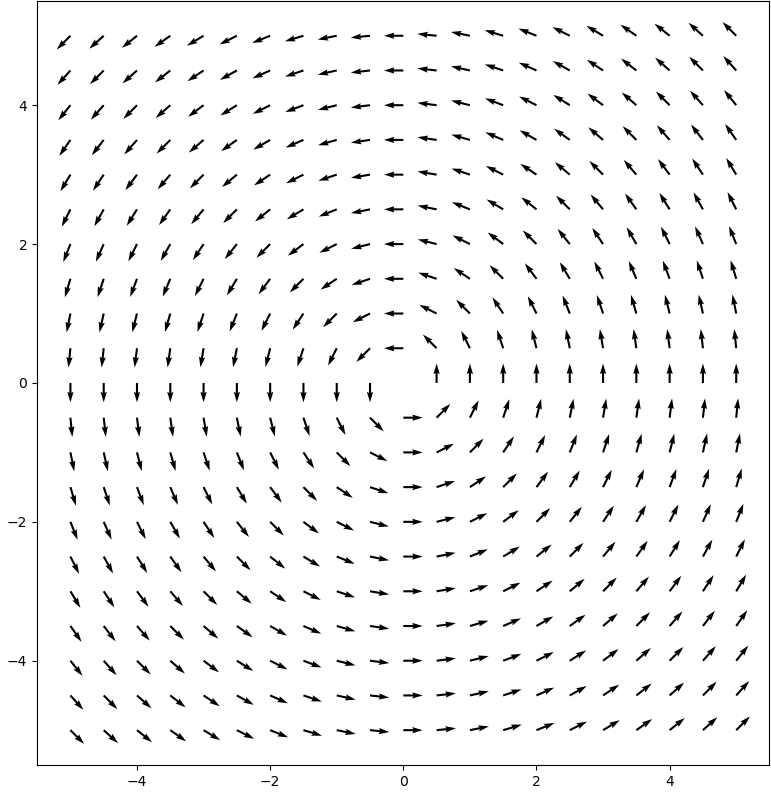
because the magnetic field is constant (specifically, 0) and the Maxwell-Faraday equation means it doesn’t have any curl. At this point, the electric field can only look like

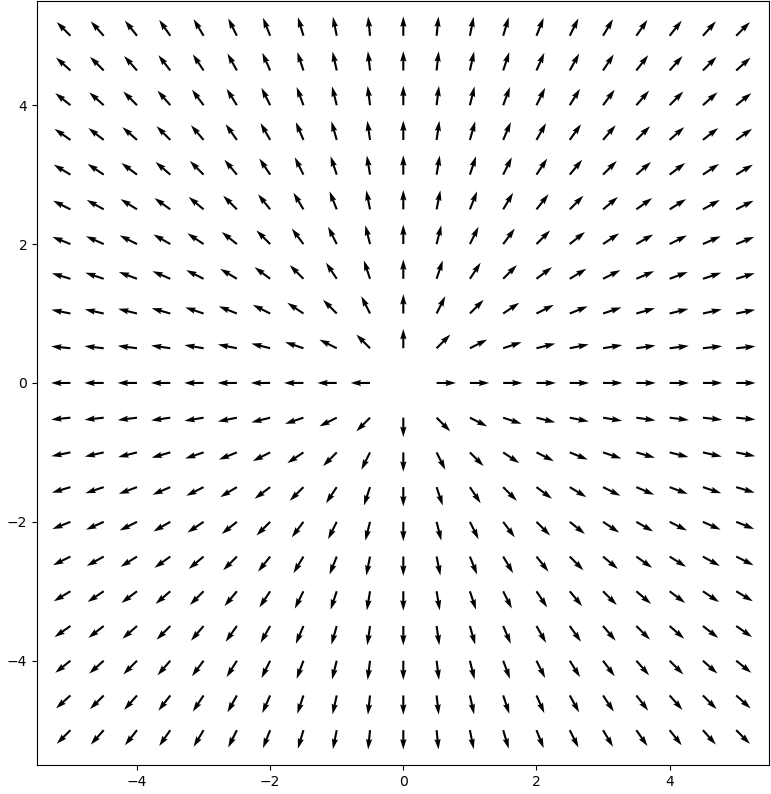
with the wire coming out of the screen. The length of the arrows will vary, but this is the correct direction.

At this point, we now know we’re looking for a surface you can rotate around the wire or slide down the wire, which means we can use a cylinder centered around the wire as our surface. Gauss’s Law for us in this case is therefore

The charge contained within a cylinder of length L is just Lλ, so there’s the right side of the equation solved. The total flux through the surface is the sum of the flux through both ends of the cylinder and the side of the cylinder (where you would put a label on a can). Plugging these in yields

Since the electric field is perpendicular to bases of the cylinder (use the surface normals for flux), they contribute zero flux.

Since the electric field points directly out of the side of the cylinder, the dot product in the integral just becomes a 2D integral, which is just the surface area of the side of a cylinder. At this point, we can get the answer with some algebra.

With experience, you’ll recognize the cylindrical symmetry, at which point you’ll be able to go from Gauss’s Law to the math with little effort.

Use Conserved Quantities

Although you can use forces and torques to figure out how anything in Classical Mechanics will move and therefore figure out other related quantities, doing so can be a pain. If you’re trying to find out how fast a ball rolling down a straightramp (without slipping and air resistance) is going at the bottom of the ramp, then you could use forces and torques even if they’re more work.

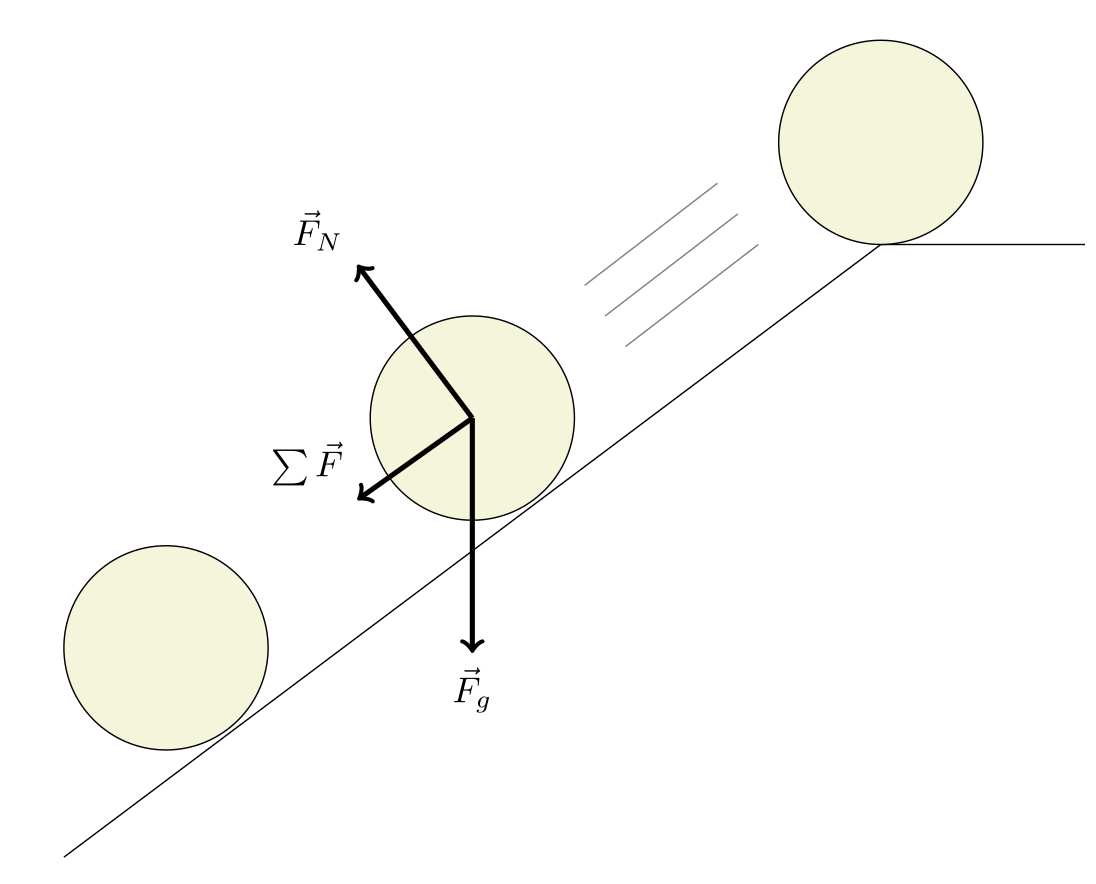
If you’re trying to find out how fast a ball rolling down a curved ramp (without slipping and air resistance) is going at the bottom of the ramp using forces and torques, you will have to do a path integral of the force, which changes depending on the position, so good luck.

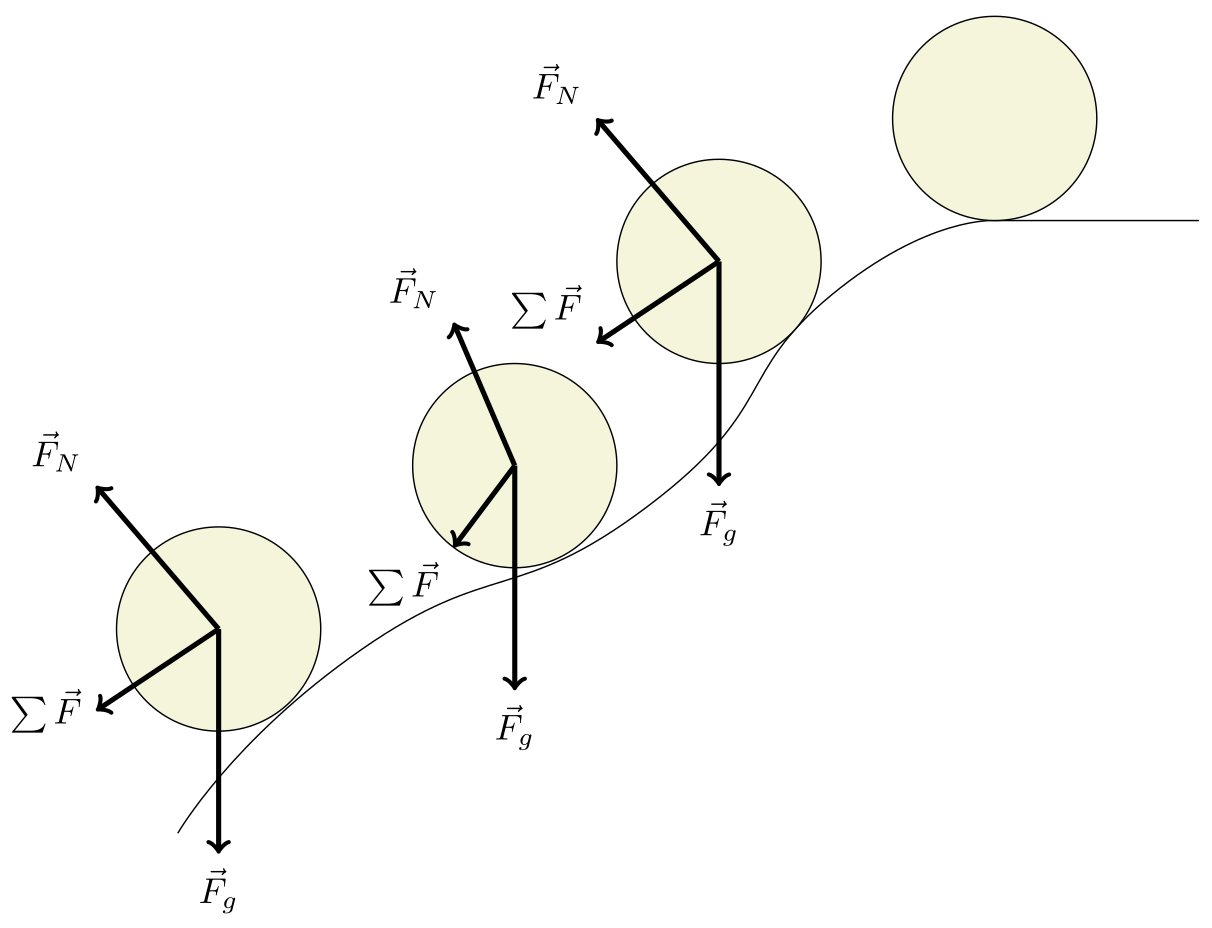
At best, even if you get a solution, you’ll have spent way more time on a problem than you needed to. Instead, looking for conserved quantities can get you an answer you can check quickly. The three most common conserved quantities in Physics I problems are

• Linear Momentum: No net external forces on the system means the total linear momentum is conserved.
• Total Mechanical Energy: No air resistance, slipping, friction, or damage to the objects in the system likely means the total mechanical energy of the system is conserved. In more technical terms, if all the forces at every point form a conservative vector field, then energy is conserved. If the problem specifies an elastic collision, then total mechanical energy is also conserved.
• Angular Momentum: Something will be rotating and there will be no net external torques.

If you can get either linear or angular momentum conserved, you get an equation for each relevant dimension. Likewise, if energy is conserved, you get one free equation, but that equation will often get you a lot more information for less effort.

Example: Momentum and Energy Conservation

An astronaut in space knocks a ball at position (-1, -3) into another ball of equal mass at position (0, 0), which then goes on to hit the wall at position (2, 3). Before the collision, the first ball moves at velocity vi. What are the velocities of both balls immediately after the collision? Assume no friction, no air resistance, no gravity, and no rotation.

Mechanical energy is conserved since the problem told us the collision was elastic, so that will get us an equation. We can also get some equations from momentum conservation since there are no external forces after the astronaut hits the first ball. We have three unknowns:

• v1, the velocity of the first ball
• v2, the velocity of the second ball
• the direction of the first ball after the collision

We know the direction the first ball went before the collision because it went from (-1, -3) to (0, 0). Similarly, we know the direction the second ball went because it went from (0, 0) to (2, 3). Next, we’ll normalize these vectors (dividing them by their length) so we end up with just the direction. We’ll put a ^ over these vectors so we’ll know they’re unit vectors.

We went through the same process for v2 as we did for vi. Now that we have the unit vectors, we can express the vectors as the product of a magnitude and a direction.

After this point, I’m going to keep everything in variables and I’m going to work with vectors because doing so will allow me to work on both the x and y dimensions at the same time because math is pretty useful. We’ll look at the momentum equation first.

Now that we have an explicit equation for the v1, we can then look at the total mechanical energy equation. Note that since v1 is a vector, we can dot it with itself to get its magnitude squared, which is what we’ll need for the kinetic energy equation.

Since the dot product between the hat vectors is a scalar (specifically the cosine of the angle between vi and v2), I’ll replace it with the symbol C to clean up the math.

Now, we plug it into the total mechanical energy equation and we should end up with something we can solve.

We reject the v2 = 0 solution because we know v2 is not zero, so we’re left with the other solution. We plug our result for v2 back into our equation for v1 and we’re done.

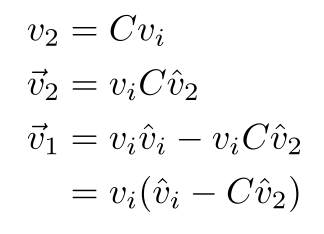
Example: Energy Conservation

A ball of mass m and radius R with a uniform density starts rolling down a ramp (not necessarily flat) with no air resistance, no slipping. The ball has an initial velocity vi before it reaches the ramp. The top of the ramp is h meters above the bottom of the ramp. How fast is the ball going when it reaches the bottom of the ramp?

Sometimes, these problems have way more information about the ramp, but you won’t even need everything that I have given you in this problem. Since there’s neither air resistance nor slipping, we can use energy conservation. We have gravitational potential energy, translational kinetic energy (mass and velocity), and rotational kinetic energy (inertia and angular velocity) at both the start of the ramp and the bottom of the ramp. For reasons too complicated to get into here, only differences in potential energy matter, meaning we can arbitrarily say the potential energy at the bottom is 0 to make our math easier.

Since it’s not slipping at any point, Rω = v at every point, meaning we have two more equations that relate the velocity and angular velocity: one at the start and one at the end. Lastly, we’ll need to know the moment of inertia for a sphere, which we can find either through direct integration or by looking it up.

Plugging everything into the energy equation yields

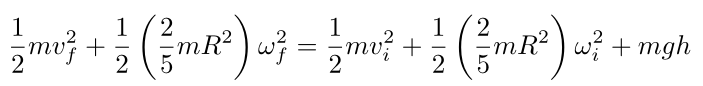
We can cancel out the mass everywhere since it’s part of each term.

We can also use the Rω = v substitution to reduce the number of variables to one unknown and three given variables. We can then solve for the final velocity. The entire process looks like

You might be a little weirded out because you might think that the final velocity should depend on mass or the radius of the object, but it doesn’t. Remember that there is no air resistance in our situation and the only energy being added to the sphere comes from gravity, which provides a constant acceleration to all objects regardless of mass. Likewise, the larger radius means a higher moment of inertia, but since there is no slipping, the angular velocity, velocity, and radius are constrained in such a way that the rotational kinetic energy is independent of the radius.

Finding a Generalization

If we let c be the ratio between the moment of inertia and the mass times the radius of rotation squared, we can come up with a general solution

If the object had no moment of inertia or was unable to rotate (say a box sliding down a surface without friction), we would end up with the standard kinematic equation

which should help you feel a little more confident about the solution.

Know Your Derivatives

This technique has a slightly incorrect name, as Know the Fundamental Relationships Between Various Quantities would be more precise, but most of these relationships are defined in terms of derivatives (or equivalently integrals), so I decided to emphasize that part. All five of the kinematics equations can be derived from the fact that velocity is the time derivative of position, acceleration is the time derivative of velocity, and the assumption of constant acceleration. Other important Physics I relationships are

• Force is the time derivative of momentum and the negative gradient (a generic spacial derivative that can be expressed in different coordinate systems and any number of dimensions) of potential energy.

• Torque is the time derivative of angular momentum.

• Work in a non-rotating system is the path integral of force with respect to position.

• Work in a rotating system is the path integral of torque with respect to angular position.

Don’t Plug Numbers in Until You Have to

Because I’ve been using this technique throughout all my examples, I won’t give an example of this guideline.

Keeping everything in variables has several benefits:

• You can kind of tell if an answer makes sense by changing the given values to their logical extremes. For example, if the force of gravity goes up as you move away from a mass, you probably made an error somewhere.
• It’s much harder to find which specific step led to an error in a series of arithmetic operations than it is to find an error in a series of algebraic operations.
• Variables will often cancel out leaving you with a simpler equation and less work to do.
• As we did in the An Advanced Trick section, both examples in the Look at Each Dimension Individually section, and the Energy Conservationexample, you can often find parts of the expression that you can convert into something you already know and reduce the amount of arithmetic you have to do.

You can generalize this principle to things like not expanding everything out until you have to, such as not breaking things into individual dimensions until you have your equations, not expanding factored polynomials, etc. You should also look for simplifications you can make in the math, whether by factoring out variables, making the variables dimensionless, introducing constants, etc.

Odds and Ends

These techniques or concepts are either too specific to get an entire section or don’t need a full explanation, so I’m going to list them off here.

• Tension is a transfer of force from one side of a rope/chain to the other, so you can add up all the forces on one side of the rope, get its magnitude, add up all the forces on the other side of the rope, get its magnitude, and then find the difference to find the net force.
• Waves, fluid flow/pressure, and oscillatory motion like pendula (neuter plurals end in ‘a’ in Latin), springs, and orbits at the Physics I level are described with algebraic equations, but they become differential equations in later classes. For now, stick with the algebra versions.
• Physics is mostly math with a few specific facts and equations as a base. Learning math will give you new methods, shortcuts, and a deeper understanding of physics. For basic physics (momentum, energy, forces, torques, etc.), I suggest learning some basic linear algebra (vectors, dot products, and cross products), trigonometry, and single variable calculus. For basic electromagnetism, I suggest learning multivariable calculus (usually Calculus III in the US). For anything after that, I suggest learning ordinary differential equations and partial differential equations.
• Be consistent. If you decide that the positive y axis will point down, then gravity will provide a positive acceleration. If you decide that W is the work done on a system, then U = Q+W. In general, once you decide the setup, you can do the math without thinking too hard and interpret the results based on your set up.

Angular Kinematics

Angular quantities were my least favorite parts of Physics I because their problems were linear problems with a few more steps or equations tacked on, so I’ve avoided using problems with angular quantities as examples to keep this article from being too long.

• All the angular kinematic quantities (angular distance, angular speed, and angular acceleration) are the normal linear quantities divided by r, or the distance away from the axis of rotation, and they have the same kinematic equations.
• Angular momentum, angular velocity, and torque are all vectors (pseudovectors are still elements of a vector space) whose direction is the axis of rotation, so you can do things like add them together and separate them into separate dimensions.
• In dealing with torque problems, if you don’t know the forces at a point, try finding the torque around that point since the unknown forces will contribute zero torque. For example, a ladder leaning against a wall will exert a force on the wall, but you probably won’t be able to figure out that force without solving the entire problem, so find the torque at the point where the ladder touches the wall.

Where to Go from Here

Figure out what works for you, what doesn’t work for you, what works for others, and the reasons behind all three. If something works for someone else but not you, see if it would be worth it to make it work for you and consider what you would have to do to make it work for you. For example, I tend to use more powerful math because doing so allows me to set up the problem and let the math do the work for me, and you might benefit from that approach.

Though I can give you what I know, the best techniques and guidelines are the ones you forge on your own through your mistakes, efforts, and achievements. If you want to do well in physics, take what I have given you and make it your own.

Afterthoughts

If you have learned or been learning physics, please leave any techniques and guidelines that worked for you in the comments below.

I’m considering making a series of articles with a similar format and style for other subjects, so if you liked this article, stay tuned.

Disclaimer

I wrote all the example problems based on the techniques and guidelines described. Some examples are based off well known problems, such as the range of a ballistic projectile and the object hanging from a string in an accelerating vehicle, or they are so simple that it is likely that someone else has written a similar problem, such the example given in the section Move Forward on Any Front, No Matter How Small.

I made all images using LaTeX, tikz, and GIMP.