An Unorthodox Lecture on Electric Currents

Most physics textbooks are similar. They differ (little) for the sequence and for the choice of the mathematical details with which topics are presented. Most authors and teachers do not even ask themselves why they illustrate topics that way. Apparently, there is only one way to introduce something.

I believe this is not true. At least, I find stimulating trying to find alternative ways to introduce something in a different way. It is a difficult task, of course, and that is, maybe, why it is rewarding.

Let me be clear: I am not stating that alternative ways of teaching something are better than traditional ones. They are just different. Someone may appreciate them, some other may not. Nevertheless, it is always good to have a choice.

What irritates me most, when I read a physics textbook, is when I read statements devoid of any experimental or theoretical justification. Often, physics laws, as well as definitions, are just given as obvious, straightforward or necessary. Seldom, they are accompanied by a “it can be shown that” introductory sentence whose meaning is, more or less, “you cannot understand why, but trust me”. I use this sentence too, in fact (recently, I used it in a story about numerical integration), however, I tend to use it to skip a formal demonstration, and I always try to justify the results using qualitative arguments. In any case, as a last resort (and, of course, in these cases, I am irritated with myself).

Among the most irritating definitions I find in almost any physics book, is that of electric current: a flow of electric charges in a conductor. Where this definition comes from? How do we know that actually a flow of particles carrying some electric charge is responsible for current? Why we define it as dq/dt, the amount of charge dq crossing a surface in a time dt?

There are, of course, good reasons to believe this. I will not summarise the story that led physicists to define such a quantity (also because, I must confess it, I do not know it very well, having found no rigorous reconstructions in the literature). I will try, instead, to find an alternative way to introduce the necessity of such a quantity, which also has the advantage of recalling another important topic (thermodynamics) that is usually left aside when we talk about electricity and magnetism, giving the (false) impression that it is completely unrelated to the others.

Let’s start with a simple experiment: connect the two plates of a charged capacitor or the two terminals of a battery using a conductor. The whole circuit heats up.

Thermodynamics tells us that the increase in temperature is connected to the increase in circuit’s internal energy by

dQ is the heat transferred to the circuit, which, in this case, is manifestly dQ=0: there are no heat sources in the vicinity of the circuit. As a result, the increase in internal energy must be ascribed to some work made by something outside or inside the circuit. A work dL is the (scalar) product of a force F times a displacement dx: in this case there is only one force that we can imagine is acting on the system. It is an electrical force, because it is only seen when the conductor is connected to a voltage source, thus it must be proportional to some charge q,and can thus be written as F=qE, where E has the dimensions of an electric field. dx is the displacement of the charge. The minus sign conventionally expresses the fact that the work is done on the system and we can, from now on, ignore it. What is important for us is, in fact, its magnitude. Thus, we can write

Power is defined as energy per unit time. The power needed to heat up the conductor is thus

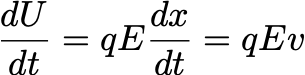
where v=dx/dt is the velocity of the charges. This suggests that charges move, with velocity v, inside the conductor. We can also write

where the line integral of E along the circuit is the voltage difference ΔV. We can thus call (define) the ratio dq/dt=I the current. It is defined such that the power is equal to IΔV. Its definition, thus, can be suggested by the above formula.

I find this introduction of this new quantity, the current, quite elegant, because it follows from first principles. It also makes it clear that the current flowing in a conductor is limited by the power involved.

At least part of my students finds it interesting: they know from high-school what a current is, but they never suspected that it was possible to apply the first principle of thermodynamics to electrical circuits. Such an introduction, thus, shed some light to this important physics law, and they start thinking at it as something that goes well beyond the physics of the gases and heat exchanges.