If you have ever taken an introductory calculus class, then at some point you were given a list of derivative rules and expected to memorize them. Today, I want to prove and show you an easier way to use the product rule and the quotient rule. Let us start with the product rule.

On a brief historical note, Gottfried Leibnitz, one of the founders of calculus, is credited with the invention of the product rule. He initially wrote down this formula using differentials, but for the sake of brevity, I will also be using prime notation, which was pioneered by Joseph Lagrange.

By all accounts, this version of the product rule works, but just because something works doesn’t mean there isn’t scope to improve.

Here is a quick proof of the product rule for the uninitiated. (If you are familiar with the proof, skip this section)

To evaluate this limit, we need to get creative and add by 0.

We can split this limit into two computable parts.

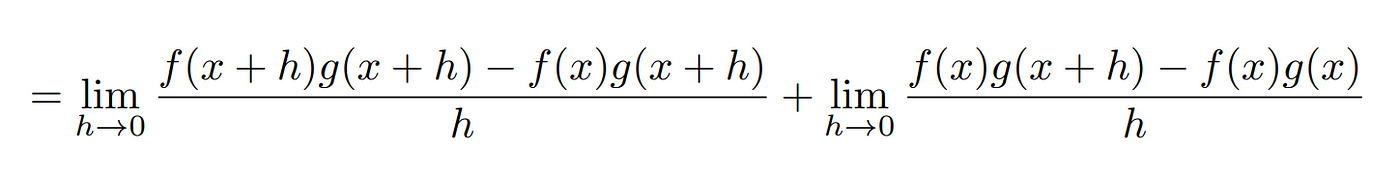
After this, we need to use the product rule of limits to simplify.

Now, we can pull f(x) outside the 2nd limit because f(x) does not depend on h, which is the variable being pushed to 0 by the limit.

This has led us to the standard product rule on formula charts.

An Easier Version

What if we divided the original function from the derivative. We get-

By simplifying, we end up with-

What intuition does this give us?

I believe this helps us divide a derivative into two essential parts: the magnitude and the “unit” change.

The magnitude or multiplier scales the “unit” change to match the value of the derivative for some x value.

The “unit” change can be thought of as a summation of ratios. I call it “unit” change because the rate of change of each function is scaled down by the magnitude of the original function.

Benefit #1: Versatility

A major benefit of this formula is its versatility. Let us try to derive the quotient rule using this formula. We can start of with y = f(x)/g(x). Taking the derivative, we get:

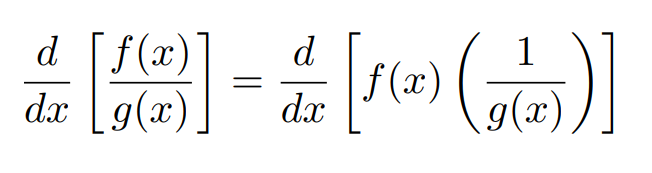
Now, using the new formula, we get:

Now, this expression is extremely unpleasant, so breaking this up into pieces would be beneficial. First, let us try simplifying the derivative of 1/g(x) using the chain rule:

Plugging this simplified derivative back into the original formula, we get:

Which simplifies to:

I find this version of the quotient rule helpful because it is the product rule with the sign flipped for the g’(x)/g(x) term because g(x) is in the denominator. This should intuitively make sense because if g(x) increases faster relative to f(x), the overall value of the derivative should decrease.

Benefit #2: Expandability

Another benefit of this formula is easier to expand when more than two functions being multiplied together. Let us take a look at how this plays out.

Similarly for the quotient rule:

Drawback: Continuity and Differentiability

Combining benefit #1 and benefit #2 can help simplify complex questions, but this comes at a cost. For example, let’s take the derivative of x³sin(x)/2ˣ.

Now, the expression might be the factored, but it is technically not equal to the actual derivative. This is because if our current dy/dx is undefined if evaluated x = 0, π, 2π, 3π, …, nπ, … . This is because we are dividing by x³ and sin(x), and we cannot evaluate dy/dx whenever x=0 or sin(x)=0.

Although not rigorous, to solve this issue, we could multiply inside the parenthesis by a factor of x*sin(x), which allows us to evaluate dy/dx at x=0, π, 2π, 3π, …, nπ, … . Hence, our final answer is-

Now, let’s try taking the derivative of y = tan(x)/(√x³).

To figure out if we have to expand this expression, we need to find the domain of the original function. Since sqrt(x³) is in the denominator, we know x >0. Also, tan(x) is undefined when cos(x)=0, so the domain of the function y is when x > 0 and x ≠ π/2, 3π/2, 5π/2, … (2n+1)π/2… .

These domain restrictions also apply to dy/dx, however, dy/dx has an extra sin(x) in the denominator, which adds more domain restrictions. Hence, we have to multiply tan(x) inside the parenthesis so dy/dx can be evaluated for all valid x-values.

The main takeaways from this article should be 3 formulas:

Conclusion

I found this trick interesting because it offers an elegant way to express derivatives that would otherwise be tedious to write down. Also, I believe this formula should become the new standard because it is easier to remember and more intuitive.

Thank you for taking the time to read my article. Please consider subscribing if you would like to read articles like this. For now, goodbye.