About Euler’s Identity

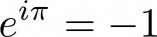
It is so famous and well-known, that I feel adding any praise to it would only decrease its value :) It is often cited as one of the most beautiful equations ever, by maths funs and others as well. But few people understand it. Be honest: do you really know what it means? In this article I’ll try to give my contribution to shed some light on it. It is a very good brain training.

Let’s write it down and taste it, wonder about how it feels like:

There is π, which reminds of circle, maybe some trigonometry (uff ;), then the mysterious i, the imaginary unit, which is not so “fictitious” (and does not equal √(-1), as you may know from my previous article “There is no such thing as √(-1)”. Then there is e, also a bit mysterious, what I remember to be connected with logarithms — those magic constructions which can transform multiplication into addition. Well, this comes in handy here: you remember, from a complex number definition/property: if (r; φ) and (s; θ) are 2 complex numbers in polar coordinates, their product multiplies their radius and adds the arguments:

(r; φ)·(s; θ) = (r·s; φ+θ)

Well, multiplying 2 exponentials does the same (with the arguments):

so this gives some hint on why exponentials and complex numbers are somehow connected. But the last formula is true for any a (real or complex), so what’s the involvement of e here? What is this e, after all?

Let’s see the following compound interest problem.

An account starts with $1.00 and pays 100 percent interest per year. If the interest is credited once, at the end of the year, the value of the account at year-end will be $2.00. What happens if the interest is computed and credited more frequently during the year?

Let’s say it is credited twice a year. We also assume that the interest rate is equally divided, so 50% per half year. For the first half year, we’ll get $1.50. For the second half year, we get 1.5 of the already credited amount, so 1.5·$1.50 = $1.00 × 1.5² = $2.25 at the end of the year. Compounding quarterly yields $1.00 × (1+1/4)⁴ = $2.441…, even more, although not very much. Compounding monthly yields $1.00 × (1 + 1/12)¹² = $2.613…, while if we calculate it daily, $1.00 × (1 + 1/365)³⁶⁵ = $2.7145…

You can see that the final amount steadily increases, but it has a limit, which is approximately 2.71828… This constant is called e, and we introduced it by one of its definitions:

Now, a question. What would be the credited amount after a continuous interest, if the account started to pay 200% interest per year, instead of 100%?

It is easy to see that it is going to $1.00 × (1 + 2/365)³⁶⁵, or in general to

But

By analogy, we can say that

what we extrapolate for any real x.

This exponential function, f(x) = eˣ has some very interesting properties. Let’s calculate its derivative.

The limit on the right of eˣ does not depend on x, and is a constant. To calculate it, we’ll resort to the binomial theorem:

The kth term of this sum is

where the expression on the right approaches 1 as n →∞. Therefore

This is the famous power (Taylor/Maclaurin) series for e. It converges for all real x. Back to our expression

We just proved that

so the eˣ exponential function is equal to its derivative. Splendid! That means that the slope of the function (its rate of change) at any given point is equal to the function value at that point.

Now if I tell you that this is the only one function with this property, you might appreciate even more the beauty of e.

Let’s see what it looks like to differentiate a more general exponential, say aˣ . If a > 0, we can find for sure a number b such as a = eᵇ . Then

Now we’ll use the power rule for differentiation:

We defined b with a = eᵇ, the exponent to which e must be raised, to produce a. This is called the logarithm of a, and because the base is e, the natural logarithm, denoted by ln(a). So we have

So in general the derivative of the exponential function at any point is proportional with the function value at that point, the factor being ln(a). This holds for all real and positive a: a > 0 (the logarithm is defined only for positive numbers), and real x. If a = e, then the factor vanishes, since ln(e) = 1. Now we can see that the number e is indeed privileged in calculus!

Let’s now move a bit from real calculus and consider the following function:

f(x) = cos(x) + i sin(x)

This function converts a real number, x, to a complex value, so it is a complex valued function of a real variable. Before going further, I’d like you be sure to understand this function. Question: where will the function values fit in the complex plane?

Depending on how complex numbers were introduced to you, you can arrive to the solution. The following figure shows the result.

The function values can be represented as points, all on the unit circle, having radius 1. P represents a typical point. Its projections on the axes are cos(x) and sin(x), respectively. And what is x? x is the angle formed with the real axis — in radians. x is the length of arc QP in the figure.

Now we’ll derivate function f(x). Yes, we can derivate complex valued functions, if they are well defined. In our case, this is easy:

f(x)’ = (cos x + i sin x)’ = (cos x)’ + i (sin x)’ = -sin x + i cos x

We used the differentiation rules for trigonometric functions. But

-sin x + i cos x = i (cos x + i sin x) = i f(x), since i² = -1. So

f(x)’ = i f(x)

Exercise. Show f(x)’ for a given x on the complex plane.

Now we’ll write

(we have already encountered this above), and taste a little bit these two formulas. What do they tell you?

Yes, the similarity is striking. If we substitute b = i and f(x) = eᵇˣ, then it looks like everybody will be happy and we proved a formula for f(x): f(x) = eᶦˣ . Hooray! So let’s do it. Or… maybe not?

No. I am sorry, but we cannot do that. Why? Because b, in the exponential derivative must be real. We cannot just take any formula, and substitute a variable with i, the imaginary unit. (If you catch yourself doing that on a large scale, watch out.) We do not have a definition for a complex exponential, i.e. a number raised to a complex or imaginary exponent. Yet…

But yes, we can do something. If we define

then

which behaves like the derivation of real exponentials. And we have, of course, the property of multiplication, which adds the arguments:

so everything fits perfectly. Any complex number can be written as z = a + ib, or

where r is the modulus, and φ the argument of z. So this is just another way to write the complex numbers (and do calculations with them). And one more thing:

I hope you enjoyed this journey. I know, you might feel a little bitter taste, because we have defined eᶦˣ, and not proved it, as you might have hoped for. But this is how math works: everything must be properly defined. That’s why it is called Euler’s formula, and not Euler’s theorem. Still, it is a very profound insight and definition. Euler was, with no doubt, a genius.