A Titan Among Men, Ron Graham

In this time of deep political, economic, and public health crisis, another terrible ill has recently befallen us: the death of a great and prolific mathematician, Ronald Graham (1935–2020).

We were blessed with his presence and genius from October 31, 1935 to July 6, 2020. While this is truly a sad moment for mathematics, I would like to honor his work and legacy with a reflection on his most notable achievements, and⁠—as someone who was helped to love mathematics by his work⁠ — this piece appreciating the beauty and poetry of mathematics itself, a beauty and poetry for which his work created new heights.

Graham was known best of all for one of these quite literal new heights: the eponymous Graham’s Number. Indeed, it is difficult to express with mere words the magnificence of it. In fact, I’m still such a novice to higher mathematics that I don’t fully understand the problem it was intended to solve, however, grasping the magnitude of the number itself helped me appreciate numbers in the same way that Georg Cantor’s work helped me to appreciate philosophy of mathematics and set theory as a philosophy undergrad. It is a token of extreme conceptual beauty.

Important also to Graham’s legacy was the popularization of the Erdős number, after the prolific mathematician Paul Erdős (1913–1996), which represents the lineage of mathematicians who have published in connection with him. Erdős published more work than any mathematician in history and often partnered with others, one of whom was Ronald Graham; Graham’s Erdős number is 1.

Graham also served as the president of mathematical organizations, namely the American Mathematical Society and the Mathematical Association of America, and was awarded the Steele Prize for Lifetime Achievement, the Pólya Prize, and the Euler Medal, as well as many other accolades. He taught at the California Institute for Telecommunications and Information Technology and the University of California, San Diego. He lived to 84, but his work will live forever. Thank you so much for your contribution and influence, Ron. It will not be forgotten.

We begin with nothing. A nothing of great significance, a nothing that is quite a something: 0. We all understand zero, particularly as the lack of quantity. It is the number of origin. An intuitive idea, but an extremely powerful one that undergirds all of mathematics.

It is not a far move from zero to imagine the presence of quantity: in the natural numbers, that being the number 1. Also a deceptively simple yet profound concept that yields infinity, used as a stepping stone to other numbers: given a number n, we can think of a function S such that S(n) = n + 1. When n is 1, S(n) is 2. When n is 2, S(n) is three. But within the basic operation of counting, we can eventually arrive at the beauty of limitlessness.

We all know how to count from here. We can count by 5s, 6s, 7s, 8s, 9s, 10s, etc. We can count to 84. We can count to 100. To 1000. These are all numbers we are familiar and comfortable with. We can keep adding 0s to the tail end of our numbers, creating ever-greater orders of magnitude.

We may even be comfortable with millions. Billions. Trillions. But somewhere in there, we have lost the sheer size of what these words mean. Most people don’t understand what a million is and what a billions is, or of course even what a trillion is. A simple comparison can put it into perspective.

You understand what a second is, what length of time that represents: a unit equivalent to 1000 milliseconds and 1/60 of a minute. But imagine now, how long is a million seconds? Or rather, if you made $1/second ($3600/hour), how long would it take you to become a millionaire?

The magnitude of a million, in seconds, is 11.57407 days or a little over a week and a half. Hold that thought in mind. I’ll get my next paycheck in about a week and a half.

Now I ask you, how long would it take you to become a billionaire? At a dollar per second?

Over 31.5 years. I myself have not lived to even feel a billion seconds (though I write this having just crested my 9000th day). Appreciate for a moment the size of a billion, measured in value over time, and feel the difference in just that order of magnitude. Where most people lose the intuitive grasp of growing numbers somewhere in the millions, this apt comparison can keep the grasp from floating away with a billion.

And now, even better: what about a trillionaire?

You would have had to start accumulating funds all the way back at the later cusp of the Pleistocene, long before human civilization had begun to manifest in Mesopotamia. Keep that token in mind as we climb this ladder. [insert sideways comment about trillion-dollar companies].

We can take a magnificent bound from here using exponents. A billion is 10⁹. A trillion is 10¹². Many of us will have heard of a googol: 10¹⁰⁰. That’s a 1 with 100 zeroes to the right of it. We have now effectively floated outside of our everyday comparisons. To appreciate the boggling vastness of a googol, consider that if the entire universe were filled with sand, the number of sand grains would still be less than a googol. And not only that, but you would need about 100,000 more equally-sized universes to fit a googol grains of sand.

But amazingly enough, we can venture outside the limits of our physical universe, and many of us will also have heard of a googolplex: that is, a 1 with a googol zeroes to the right of it, or 10 to the power of 10¹⁰⁰. The greater we go, the more difficult it is to find comparisons for perspective. But, thinking about the Hot Big Bang, we may ask the question: how long would it take for all of the heat energy in the universe to fizzle out and leave the entire expanding universe cold and dead in a Big Freeze? The answer is about 10 to the power of 10⁷⁵ years, notably less than a googolplex.

Enter Ronald Graham.

Graham’s number makes a googolplex look miniscule. Without the label itself that we use to refer to the number, it is physically impossible to imagine: your head would collapse into a black hole if you did.

Now if that’s the case, how in the hell did Graham come up with it? Let’s take a step away from numbers themselves to appreciate relationships between them: operations.

I said that with the number 1, you can reach infinity. You can use the successor function, which is appallingly simple. You’re just using addition, and you say, “Hey let’s start with some number, and since we already have 1, we’ll go with that. What do you get if you add this number to the one we have? Hm. We get 2.” Of course. But now you can repeat that as many times as you like, and reach any number in the natural counting numbers (including Graham’s number, by the way). Merely addition, ad infinitum.

But now let’s take 3, which is the number Graham used to get to his eponymous number. And let’s use addition. And let’s use the successor function, but change it a bit: S(n) = n + 3. So now we’re just counting by 3 instead of 1: 3, 6, 9, 12, 15, and so on. Notice an interesting thing about this: these are simply multiples of 3. So we could just as easily say that the number of times we perform this function is the same as multiplying 3 by that number. Hold that thought.

Let’s adjust the function a bit. Notice another interesting thing about certain numbers along the way, if you kept this function going: not only are they multiples of 3, but they are also 3 multiplied by itself some number of times. Zero times? Well, you’re still at 3 (3¹). Twice? Aha, 9 (3²). Thrice? 27 (3³). A new pattern emerges: exponentiation. Let’s use that to adjust this function, although we need a different notation to make it clear: a to the power of b, or a *a * … * a * a (b times). You get the idea.

Now here’s another idea, which you may have already noticed: what if you take the power of something which is already taken to the power of something else? Sound familiar? A googol maybe? A googolplex? Let’s play with that.

Start small. How about 3? Squared? Nine. Or, to the power of 3? Okay, 27. But now, 3⁹. 19683. Now 3²⁷: it’s already ridiculous, over seven trillion; that’s how fast it explodes. But if you’ve followed me this far, buckle your seatbelt because the launch just started and we’re going to the moon, baby! You may notice a new pattern here, like stacked exponentiation, where we take 3 to the power of 3 to the power of 3. That’s sometimes called a “power tower” (very charming, but slightly inaccurate; won’t discuss the nitty gritty here), but formally known as “tetration”.

This “stacking” is foundational to getting to Graham’s number. Since we’re about to make a googolplex look like a speck of dust, we’re gonna need some extra firepower, and that firepower is in the notation. If you notice, each time we see a new pattern emerge in the operations, we want a new notation to condense those operations to speed up the use; imagine trying to write 3²⁷ with only addition and 1. Good luck.

The pattern we want to be describing is how many times we’re doing this stacking. And then we’re gonna take that stacking and stack with that. So we have a “stacked stacking”. Then again, for a “stacked stacked stacking”. Then again, and again, and again… Bear with me.

The new notation we’re going to think about is called Knuth’s arrow notation: each arrow is a “stacking” level, so to speak. And while it might seem scary, it’s actually straightforward. It looks like this:

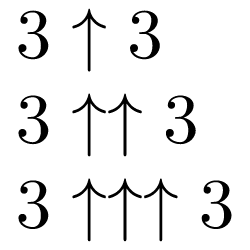
You can read them as “three arrow three”, “three arrow-arrow three” and “three arrow-arrow-arrow three” (or abbreviated: 3A3, 3AA3, 3AAA3). Start with the little guy, 3A3. He’s just 3³, or 27. His big brother, 3AA3, describes 3 to the power of3³, or 3²⁷. In general, 3AAn is stacked exponentiation (tetration) that is nexponents high.

Now, for Graham’s number, this is weaksauce. But for perspective, keep in mind that if you were making $1/second, it would take you from before human civilization to get to a trillion dollars. Now think about seven trillion. That’s a big boy. It gets better.

But first, it’ll help to give these numbers names. In the spirit of Atlas holding the world on his shoulders, let’s refer to them as the Titans. Fondly call 3A3 Oceanus. Oceanus stands on the shoulder of 3AA3, who we’ll call Tethys. This is where tetration stops, but the idea continues. We want to take that magnitude of Tethys (over 7 trillion) and build a tower as high as Tethys. This has a new term: “pentation”.

So, we repeat the process for 3AAA3, where 3AAA3 is 3 to the power of Tethys-many 3s. That means that 3AAA3 is a “power tower” of 3s that’s over 7 trillion high, and we’re gonna call this Hyperion. So Hyperion is 3 with the height of Tethys on its shoulders, which is 3 with the height of Oceanus on its shoulders. Grasp this: Hyperion is not 3 to the power of over 7 trillion. That would be much too small. Hyperion is 3 to the power of 3 to the power of 3 to the power of 3… over 7 trillion times. Your mind should be reeling, and if so, good.

Now, if you started at the top of Hyperion, and condensed each exponent down the line until you got to the bottom, you’d have an incomprehensibly large number. If you tried breaking our universe down into the smallest possible unit of volume, you would still not be able to fit this number of things into it. Crazy, right? What’s crazier is, that is still tiny compared to Graham’s number. In the words of Graham himself, “You ain’t seen nothin’ yet!”

Let’s say we now want to add a fourth arrow; this is known as “hexation”. Let’s give it a new name: Theia. Now Theia is going to be a pentation of Hyperion.

Let that sink in. This is staggering. Hyperion being a power tower over 7 trillion exponents high, whatever godly number that comes down to is the number of pentations you are doing here. And each pentation is another power tower. So you’re starting with one tower, and that number is how high the next tower is… which in turn is how high the next tower is… which, in turn, is how high the nexttower is, which you repeat over 7 trillion times. It’s towers all the way up!

If you thought that was impressive, it gets even bigger. What Graham did at this point was create a new notation that just obliterates everything so far. This almighty number we’ve called Theia? Graham says, let’s create a new number with Theia-many arrows. You saw how drastic an explosive change just adding one arrow is. Graham then adds this obscene number of arrows to the next level, called G-1.

Now we’re “almost” to the top! Conceptually, it’s relatively simple now: we’re just adding a lot of arrows. Graham does this 64 times. G-2 is two 3s with G-1 manyarrows between them. Then that gargantuan number is how many arrows are in G-3. And then G-4 has G-3 many arrows… and so on and so on, up to 64 levels! The final, ultimate Graham’s Number is G-64.

You can’t even truly wrap your mind around this. You just can’t. It’s a number so large that it simply exceeds the capture of the human intellect, outside of understanding the notation that created it. But understanding that notation, and seeing the enormity of this number, is truly humbling and stupefying. There is something powerful and beautiful about this idea.

You may wonder why Graham came up with this number. As I said, I don’t even fully understand the problem it was intended to solve, but it was essentially an upper bound on the number of dimensions that a “hypercube” could possibly be in where it avoided a certain combinatorial problem; some very abstruse higher mathematics quandary. But unlike other similarly large numbers, this one is not large for the sake of largeness, but to establish the boundaries of mathematical knowledge around a certain kind of question. That was Graham’s genius.

When I first discovered this number, I was absolutely astonished, and it helped push me from my lukewarmth about mathematics into a boiling fascination. It reignited the sense of awe that I had found in my advanced logic course during undergrad when I learned about Cantor’s Theorem.

I won’t go into Cantor’s Theorem here, except to say that infinity, of course, makes Graham’s number also look infinitesimally small… and Cantor’s Theorem makes infinity look infinitesimally small.

There may or may not be a Paradise after life, but we know there is Cantor’s Paradise in this life, and we sure as hell know Ronald Graham climbed into it.