As π goes, so goes a circle

π is ubiquitous both in mathematics and physics. Its appearance in some contexts are intuitive to grasp. Others require intellectual contortion, a mind-bending that defies all intuition. Wherever π appears, a circle is always hiding, to be discovered irrespective of one’s intuition! Let us get started slicing π, and explore a few astonishing cases.

The Circle

History informs us that π had an elevated, almost divine status in ancient times due to beauty of the circle, its symmetry to which this ratio owes its origin. Several ancient societies seem to have independently discovered it, and perfected its numerical accuracy for use in astronomy, architecture, religious rituals, and for deriving pure mathematical pleasure.

It is customary to think of π in the context of a circle. We learn in school that the ratio of the circumference (C, c) of a circle, is proportional to its diameter (D, d). No matter the size of the circle, this ratio (C/D = c/d) is constant. The constant of proportionality is labeled “π”. It is a beautiful transcendental number with a value 3.141592... Any number that can conceived is said to be found in the decimal expansion of π, including the digits in your birth day!

Dropping Needles

Suppose we drop a needle on the floor. Assume the floorboards are rectangular, equidistant strips as shown in the picture. What is the chance of it landing across a line (gap) separating any two strips?

Georges Louis Leclerc was an eighteenth-century naturalist, mathematician, and cosmologist. He inherited his family estate to become Comte de Buffon. He is said to have stated the problem in 1777.

It’s innocuously couched, asking for the odds of a needle intersecting with the gap in the floor strips. At first blush, its connection to π is not obvious. As we will see, it not only has an intimate connection to it, but by counting how often it intersects in repeated trials of dropping the needle, one can estimate the numerical value to which this ratio (i.e., probability of hits) converges. The circle around the needle in the picture is a dead giveaway!

The floor-strip-width (w) and needle-length (l) certainly factor in whether the needle intersects with the gaps or not. In order to appreciate the connection to π, one need only consider the simplest case (l < w). The translational and rotationaldegrees of freedom of needle allow it to fall, bounce, and rotate about an axis passing through its center of mass before it comes to rest on the floor.

The floor is the XY-plane, the Z-axis sticks straight upward from the floor and the dotted line circumscribing the needle in its resting position is shown. The geometry of the problem dictates that the circle, if and when it does, must intersect a floor strip exactly at two spots with certainty, with the gap between strips forming a chord of the circle.

Solution

The chance (or probability, P) of it intersecting the gap is given by P = 2l/wπ, the solution obtained in many elegant ways found in the literature¹. Assuming Ntrials (or a box of N needles) dropped randomly on the floor, k of which land across the gap, the probability is given by P ≈ k/N as N→∞ which implies π ≈ 2lN/wk. This approach is a nifty Monte Carlo simulation that can be used to calculate the value of π.

A Pool Table

The crisp clack of the cue ball’s collision with the rack as the balls scatter is a familiar sound in the game of Pool (or Billiards). What does the game of pool have in common with π? In 1990, Gregory Galperin came up with a novel way to find the value of π as he was preparing for a colloquium talk. Unlike Buffon’s which is probabilistic, his method is a deterministic one. Before we get to it, we need to understand idealized billiard ball collisions, the so-called Sinai’s Billiards problem.

Sinai Billiards

In 1963, Yakov Sinai, the distinguished mathematician, introduced an idealized physical system. A billiard ball bounces around elastically (i.e., no loss in momentum or energy) on the surface of an ideal square shaped pool table with a small modification — an introduction of an inner circular obstacle whose center coincides with the square’s center. The ball is free to bounce in the region between the outer square wall and the inner circular wall. The ball’s movement is ergodic — meaning, if we zoom into an arbitrary area (A) the amount of time (t) the ball spends as it zigzags across it, is proportional to its area (t ∝ A). This idealization is used in studying many dynamical systems, both regular and chaotic. Not to mention its connection to non-Euclidean geometries — spherical or hyperbolic.

Colliding Masses

Take two masses (m, M) whose ratio is an even power of 10, M= km, with k={10⁰, 10², 10⁴, 10⁶, …} and assume Sinai’s billiards idealization. m is resting on a smooth floor at a certain distance from a smooth wall. It is sandwiched between the wall and the other mass M, which is moving toward it with a constant velocity. Mcollides with m, which then collides with the wall, rebounds and after a series of collisions with each other and the wall, they both eventually move away from the wall, never to collide again.

If we count the total number of collisions (N), including with each other and the wall, we get N = {3, 31, 314, 3141, 31415,…} which are digits of π! specifically for the case when the ratio of the masses k={10⁰, 10², 10⁴, 10⁶, 10⁸, …}.

Just to give an idea of the scale, there are k=10²⁰⁰ atoms in the entire visible universe. One can’t imagine reaching a precision of 200 digits with this method. Given this nature of k, nobody is quick to suggest this experiment be conducted in reality. But, it’s hard not to be amazed that the number of collisions should track the digits of π, allowing us to rattle them off to arbitrary precision — and that fact is nothing short of astounding! Where is the circle in this problem?

For k = 10⁰= 1, and m = M, it is easy to check the collisions (N = 3).

1. Collision #1: M (going ←) collides with stationary m perfectly transferring all its momentum (because m = M), which brings M to rest and sends m towards (←) the wall.
2. Collision #2: m rebounds (← →) from the wall, still maintaining the same magnitude of velocity but reversed in direction, moving right towards M.
3. Collision #3: m collides with M and comes to rest transferring all its momentum to M, which then moves away from the wall ( →) forever. There are no more collisions thereafter.

For other values of this ratio, one can simulate the collisions and count it. For M = 10²m, N = 31 and for M = 10⁴m, N = 314 and so forth. Its easy to spot the pattern of digits of π showing up in the total number of collisions.

Symmetry

Symmetry and conservation laws are inextricably linked. The conservation of kinetic energy (K.E, which is also the total energy in this ideal situation) requires that K.E = mv²/2 + MV²/2 be constant throughout the ensuing elastic collisions. Similarly, conservation of linear momentum (p) requires that p = mv + MV to be constant. Even though the velocities are changing in the momentum transfer, these quantities (p, K.E) are fixed because of Sinai idealization and elastic nature of collisions. Careful inspection reveals K.E is the equation of a circle, with pairs of velocities (v,V) yielding a given K.E, all lying on the circle. p is an equation of a line with pairs of velocities (v, V) lying on a line. The points of intersection of K.E-circle with p-line is a solution to one collision. Many parallel p-lines slicing the circle into equal arcs are solutions to subsequent collisions.

By transforming the dynamics of collisions in an abstract space called the configuration space or the phase space using (x, y) = (v⎷m, V⎷M), the problem reduces to counting the parallel chords of p-lines intersecting the K.E-circle with the collisions represented by constrained jumps from one point of intersection to the next. This three-part-video captures the essence beautifully.

Solution

The expression for number of collisions is shown in the diagram below where the arctangent of the square root of the ratio of the masses is involved. In the limiting case where one of the masses is a power of 10, the arctangent of an angle (in radian measure) is equal to the angle itself. This problem illustrates the hidden circle (kinetic energy) that results in π showing up in the result. An alternate solution using Möbius transforms is also instructive.

Infinite Series

Mathematicians have been flirting with infinite series for many centuries. It has spawned several paradoxes of motion such as the Achilles and the tortoise and Dichotomy paradox. When it comes to π, the middle ages saw several independent discoveries of infinite series sums converging to π, with one of the earliest of attempts due to an Indian astronomer, Mādhava who founded the Kerala school of Astronomy in the fourteenth century. Others include Leibnizand Gregory in seventeenth century. How can an infinite series be linked to a circle?

Mādhava-Leibniz Series

This infinite sum shown in equation (1) is special because of a couple of reasons.

• Firstly, it dances indefinitely around π/4 on the number-line to which the sum eventually converges. Upon discovering it, Leibniz felt like he had unlocked the mystery of Nature, so much that he quit being a lawyer to pursue a career in mathematics. We can appreciate why the alternating addition and subtraction of a sequence of odd-integer reciprocals had a special place in Leibniz’s heart, even though it had been discovered two centuries earlier —precisely because of its beauty and simplicity.
• A second, more elegant reason one could argue, is it ties π to the distribution of Gaussian primes that are lattice points on a circle in the complex plane. A cursory glance at the series doesn’t reveal this connection. We have to uncover a symmetry lurking inside, which makes it worth exploring. Let’s explore the second equation above which captures the essence of this symmetry. Let’s go!

Lattice

In the diagram, a complex plane is placed over a grid of 1x1 unit squares, with a total of 11² = 121 gold dots forming a lattice, each lattice point representing an ordered pair of integers. For any lattice point, say (x,y) = (1,-3) we can represent it as a complex number B = 1–3i, where i² = -1 in the usual notation. This is a deliberate choice, as we will be drawing circles and vectors centered on the origin (0, 0)=0+0i.

How many lattice points does a circle of radius r contain?

The number (N) of lattice points contained by a circle of radius r is proportional circle’s area, roughly speaking. Because of our deliberate choice in constructing the grid using unit squares, there is one lattice point per unit area. We can arrange them so that they cover the circle, except it gets a bit tricky at the circle’s boundary, without perfect coverage.

The hope is, as we make the radius larger, the patch will cover the boundary without overshoot or falling short. In the limit as r gets sufficiently large, it converges to a true number of lattice points — and this is the number we are after! The area will approximately be πr², i.e., Nr²≈ πr². “Approximately” becomes “exactly” as the radius grows larger, as the percent error between estimated number N and π gets smaller. If we come up with an enumeration algorithm to count the number of lattice points, that would then give us π.

Integral Patterns

Do all circles sit on lattice points?

There are infinitely many circles with radii smaller than r that are concentric with r. Let’s call them rings. Not all rings intersect lattice points. Some are shown in the diagram.

• By construction, rings of non-integers, r²= {3.7, 4.2, 0.78, …∞) of which there are infinitely many, don’t intersect any lattice points and can be omitted from the count because they don’t count!
• Right triangles with hypotenuse = r²={2, 10, 17}={(1²+1²), (1²+3²), (1²+4²)}intersect lattice points and form Pythagorean triplets. Others, like the yellow,orange rings with r²={7, 21}, don’t intersect any lattice points.

Gaussian Primes

Every prime number of the form 4n + 1 is the sum of two integral squares in exactly one way.

All integers, if they are not prime, have unique prime factors. A theorem by Dirichlet’s states if (a,b) are positive integers with 1 as their greatest common divisor ⇒ GCD(a,b)=1, then there are infinitely many primes of the form an+b. There are infinitely many primes of the form 4n+1 and 4n+3. All primes are odd, except 2, the only even-prime.

Consider the red ring, r²=17, that intersects lattice points. 17 is a prime of type 4n+1 (n=4) expressible as sum of two squares. r²=17=(4²+1²)= (4²-i²)=(4+i) (4-i). We can form eight Pythagorean triplets {(4,i,r), (1,4i,r), (-1,4i,r), (-4,i,r), (-4,-i,r), (-1,-4i,r), (1,-4i,r), (4, -i, r)} shown as red dots. (4±i) are Gaussian prime factors because they can’t be factored further.

The yellow ring with r²=7, is a prime of type 4n+3 (n=1) cannot be a a hypotenuse of any right triangle with integer sides, and therefore, does not intersect any lattice points. What about r²=21, the orange ring? Though not obvious, neither of its two factors (21=7ᐧ3) are of type 4n+1. Neither ring intersect any lattice points!

Symmetry

What about other integers, say the orange ring with r²=15=2²+1²=3ᐧ5. We know 5 is a 4n+1-prime. Its Gaussian prime conjugates are (2+i)(2–i) — good so far. But the other factor viz. 3 is an odd-ball that breaks the symmetry! It cannot be factored into Gaussian primes and so it will not intersect any lattice points. If we restore symmetry by introducing a factor 3 to make r²=45 shown in lime-green, r² = 45=3²ᐧ5=6²+3²=(6+ 3i)(6–3i). This guarantees lattice points! r² containing odd powers of 4n+3-primes do not get us lattice points.

What about r² containing powers of 2? Yellow ring has r²=28=7ᐧ2². Since 2 = (1+i)(1-i), any power of 2 provides a pair of prime conjugates that doesn’t affect the lattice points, so we can ignore them from the count. Since 7 is a 4n+3-prime, r²=28 will not intersect with any lattice points.

Rotations

Let’s look the set 𝓡={i, i², i³, i⁴} = {i,-1,-i,1}. This is a special set that rotates a vector in the complex plane successively by 90°. To illustrate, let’s pick the green ring, r² = 45. The prime factors are 45=9ᐧ5=3²(2²+1²)=3(2+i)ᐧ3(2-i)=(6+3i)(6–3i).

Start with (6+3i). To move to the next lattice point we rotate it by π/2 = 90° to get i(6+3i)= (6i+3i²)=(6i-3). Repeating again, i(6i-3)=(-6+3i), another lattice point! Do it again, we get iᐧ(-6+3i)=(-6i-3), and finally the fourth time, we get iᐧ(-6i-3)=(6–3i) back where we started. Using a single Gaussian prime (6+3i), we obtained a total of four lattice points around the circle. We can do the same exercise for (6-3i) for the other four. Thus, the rotational symmetry means, we simply count the number of unique factors and multiply the result by 4 (for the four rotations).

Counting Rules

We see some promising hints of lattice-point-count. Let’s summarize them.

1. Integer Rule: If a ring has lattice points, r² must be an integer.
2. Odd-prime Rule: When r² is a 4n+1 type odd-prime (i.e., r²=17), we have lattice points. When its not (i.e., r²=7), there are zero lattice points. For any other integer (i.e., r²=10) if its prime factors (2,5) themselves can be factored into symmetric Gaussian prime conjugates, we find lattice points.
3. Powers of 2 Rule: r² containing powers of 2 do not modify the number of lattice points that the ring would otherwise have. r²={10,20,40,80…} all have identical number of lattice points as r²=5.
4. Multiple of 4 Rule: All circles that intersect have total counts that are multiples of 4 due to rotation (𝓡) of Gaussian primes on rings.

Armed with these rules, can we start counting? Here’s the pattern for the lattice count so far:

Enumeration Algorithm

To obtain the number of lattice points on or inside a ring of r²=N, we have the following algorithm.

1. Find the (unique) prime factors of N.
2. For each factor: if it’s a 4n+3 type prime with even exponent, it contributes once to the count; if it’s a 4n+1 type prime, the total contribution is equal to one more than it’s exponent; any powers of 2 (the only even prime) don’t affect the count.
3. Lastly, there is a factor of 4 (rotations)
4. Repeat steps 1, 2 and 3 for all integers ≤ N

Let’s use this algorithm to calculate the number of lattice points, let’s call it 𝓛(N) for N={45, 17640}

For N=45=3²ᐧ5

1. 3=4k+3, k=0 ⇒ looking at the exponent = 2 (even) — so we get 1contribution from it. 5=4k+1,k=1 ⇒ looking at the exponent = 1, contribution is one more than the exponent, so we get 2
2. Include factor of 4, so total lattice points for 𝓛(N)= 4ᐧ1ᐧ2=8 lattice points!

For N=17640=2³ᐧ3²ᐧ5ᐧ7²

1. 2³ has 1 contribution, 3² (4k+3 type with even exponent) has 1, 5 (4k+1) has (1+1), 7² (4k+3 with even exponent) has 1.
2. Including factor of 4, the total is 𝓛(N)=4ᐧ1ᐧ2ᐧ1=8 lattice points

What’s neat thing about this is 𝓛(5) = 𝓛(45) = 𝓛(17640), rest of the contributions are just multiplied by a series of ones!

Two more examples, for N={2925, 64350}, factors are {3² ᐧ 5² ᐧ 13, 2 ᐧ 3² ᐧ 5² ᐧ 11 ᐧ 13}and contributions are {4ᐧ1ᐧ (2+1)ᐧ(1+1), 4ᐧ1ᐧ1ᐧ(2+1)ᐧ1ᐧ1} and 𝓛(N) = {24, 12} lattice points.

Dirichlet Character

This is function “chi”, 𝜒(n) with the following properties

1. 𝜒(1)=1
2. There is a positive integer k such that 𝜒(n) = 𝜒(n+k) for all n
3. If GCD(n,k) > 1, 𝜒(n)=0 and if GCD(n,k)=1, 𝜒(n)≠0
4. 𝜒(mn) = 𝜒(m)ᐧ𝜒(n)

With this definition of of the 𝜒 function (called the Dirichlet Character), the following pattern emerges:

• 𝜒(1)=𝜒(5)=𝜒(9)=𝜒(13)=𝜒(17)=…=𝜒(4k+1)=1
• 𝜒(3)=𝜒(7)=𝜒(11)=𝜒(15)=𝜒(19)=…=𝜒(4k+3)=-1
• 𝜒(2)=𝜒(4)=𝜒(6)=𝜒(8)=𝜒(10)=…=𝜒(2k)=0

What’s the point of this function? It allows us to represent 𝓛(1), 𝓛(2) … etc. which are the counts we need to tally for approximating π.

Let’s consider the same example N=45=3²ᐧ5 ⇒ 𝓛(45) = 4 ᐧ 1 ᐧ (1+1). This can be expanded using 𝜒 and written as

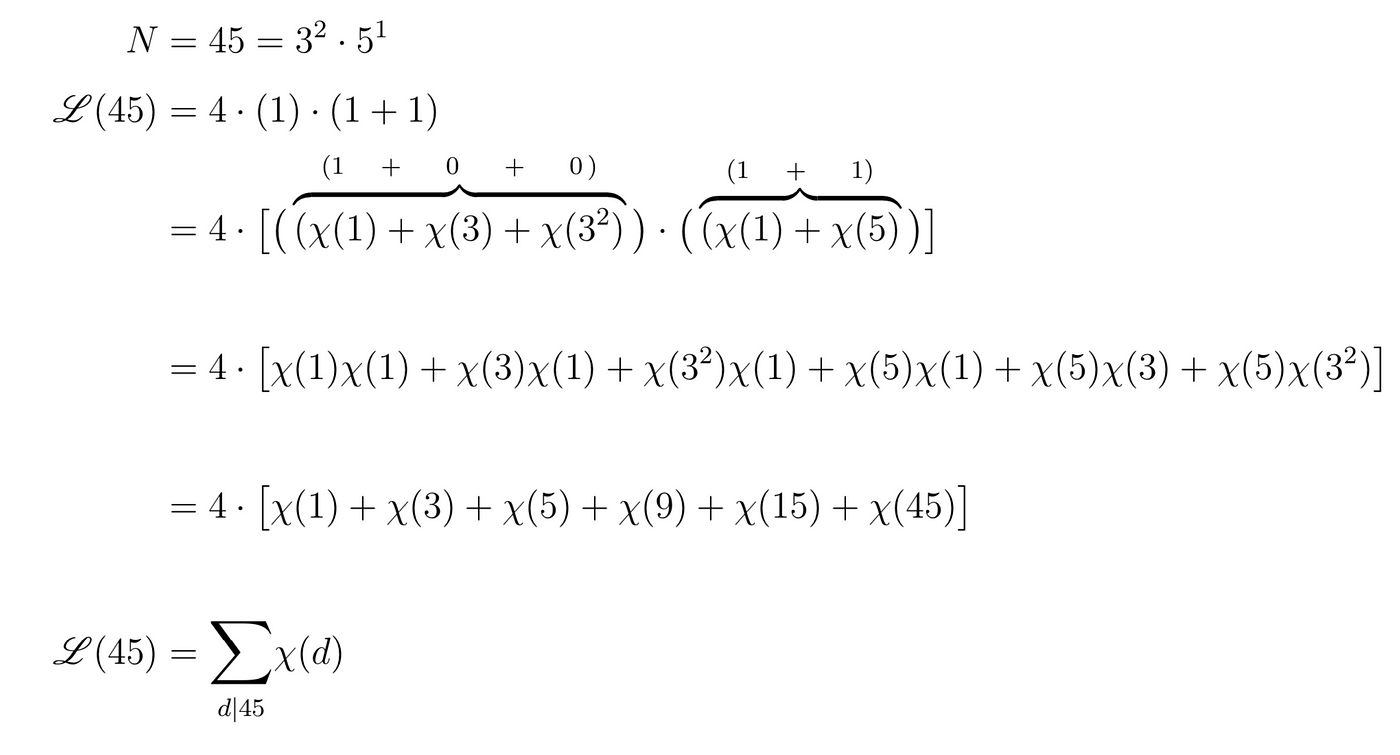
Notice how all divisors of 45 appear. This allows us to come up with a pattern of how many 𝜒(1), 𝜒(2), 𝜒(3) etc. are contained in a radius r²=N for any arbitrary N. All divisors of N appear in the count. Some numbers have a lot of factors, others like the primes have just two divisors etc. But all numbers have a divisor of 1, half of them have a divisor of 2, a third of them have divisor 3, a fourth of them 4, etc.

Solution

Putting it all together, we start making a list of number of lattice points for all integers {1,2,3,4,…10,11,…,∞} and tally {𝓛(1), 𝓛(2), 𝓛(3), …, 𝓛(10), 𝓛(11), …, ∞} as captured in this beautiful video that inspired me to write this article. We have to count all the divisors of {1, 2, 3, 4, …N}. And not forget the factor of 4 for rotations!

• For a given N, 100% of all integers in the set {1,2,…,N} are divisible by 1 so we include 1 with 𝜒(1).
• Next, about one-half (1/2) of all integers {1, 2,…N} are divisible by 2. So we associate a factor (1/2) with 𝜒(2)
• A third (1/3) of all integers {1, 2,…N} are divisible by 3. So we associate a factor (1/3) with 𝜒(3).

Then we tally over all of these sums to infinity to get the count of lattice points. This is shown below with the notation (d|n) implying all divisors (d) of n from 1 all the way up to and including n.

Beautiful π

There are many other examples where π appears including Fourier Analysis, Analytic Number Theory etc. for instance. Where it appears, we can be certain there is a hidden circle, or one in plain sight. One of the most beautiful equations in mathematics is the Euler’s Identity which has five ingredients (e,π,i,1,0) and two symbols/operations(+,=) connecting them and is one of the most remarkable appearance of π in mathematics.

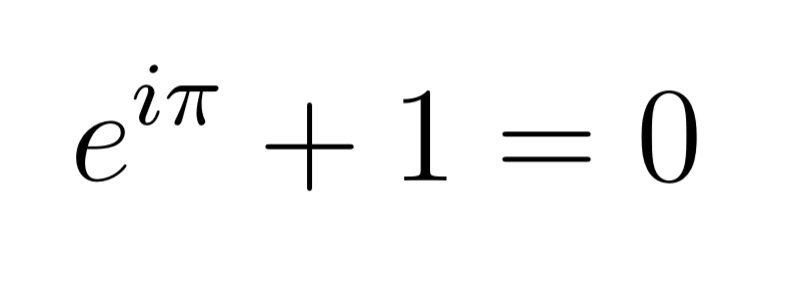
References

This article was inspired by many hours of research into π as I was coaching my teenager. Started off as a curious exercise in learning about the circle, and morphed into several small projects — including programming, simulation of π and representing it as a series. The videos of Mr. Grant Sanderson(3Blue1Brown) proved invaluable in our exploration. Thanks for reading!

1. Buffon’s needle problem: An exciting application of many mathematical concepts. Mathematics Teacher, 67 (2), 183–186, Schroeder, L. (1974).
2. Playing pool with π. The number π from a billiard point of view. Galperin, G.(2003)
3. The discovery of the series formula for 𝜋 by Leibniz, Gregory and Nilakantha, Math. Mag. 63 (1990), no. 5, 291–306. Ranjan Roy, MR 1081274
4. Why was this visual proof missed for 400 years? Fermat’s two square theorem, Mathologer, Jan 25, 2020