A Simple Proof of the Quadratic Formula Using Symmetry

Suppose you don’t remember the quadratic formula and you have to solve a quadratic equation of the form

The only thing you need to remember really is the reflectional symmetry of the parabola. The symmetry of the curve implies that the two real roots (if they are real) lie equidistant from the reflection line of the parabola.

In the above equation, we can divide through by a to get

Now, recall that the polynomial on the left-hand side can be factored into a product of two linear factors i.e.

From this, we easily deduce that

Now, what does it mean that the roots lie equidistant from some real number?

It means that there exist some numbers α and δ such that

Let’s substitute that in the above two equations. We get

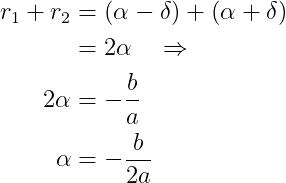
For the second root relation, we get

So we can write down our well-known formula:

We assumed that the roots of the polynomial i.e. the solutions to the quadratic equation were real but in fact, this symmetry argument also works for complex roots because in any polynomial with real coefficients, complex roots come in conjugate pairs, that is, if x+iy is a root then x-iy is also a root.

This means that complex roots are also equidistant from the same real number as when the roots were real but in the perpendicular direction, namely parallel to the imaginary axis, so our assumption about the symmetry of the roots still holds. The only difference is that when the discriminant b²-4ac is negative we get an i in front of the square root and we change the sign inside the root. The formula still holds!

Notice that the only thing you need to remember in order to derive this yourself is that the roots of a parabola (real or complex) can be written α + δ and α - δ. Once you have that, simply compare that to the coefficients using the factorization of the polynomial.

Try to derive it yourself as a small exercise. Once you’ve done that, you won’t forget it.

Also, note that any two real numbers can always be written in this way for some α and δ so if we were only after the real roots, the symmetry of the polynomial would be more of mnemonic than the reason behind this trick.

However, any two complex numbers cannot be written like that for α real and δ imaginary, but complex conjugates can, which of course, complex roots of parabolas always are, as explained above. So really, there is also complex symmetry.

By the way, the fact that complex roots of any real polynomial come in pairs immediately gives us the result that a polynomial with odd degree always has at least one real root! Because when counting multiplicity we always have the same number of roots as the degree of the polynomial. Pretty nice.