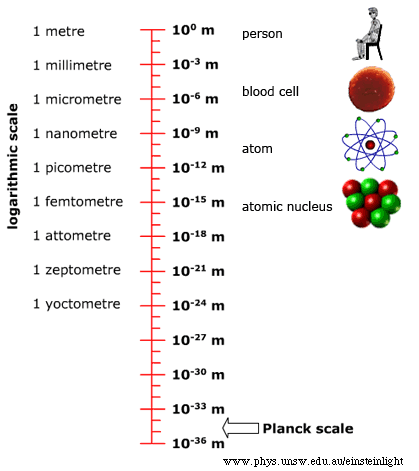
You expect the physical world around you to behave a certain way. If you knock a glass off the table, it will fall to the floor and likely shatter. How do you know this? Primarily from everyday experience, which your brain distills into your intuition. Once you’ve seen enough things fall, you subconsciously generalize that to the intuition that everything falls. Then you encounter a helium balloon, see it rise instead of fall, and you layer on conscious knowledge over your subconscious intuition. You learn about gravity and buoyancy and how to reason about an imbalance between the two causing things to rise, float, or fall. This process of understanding the typical by intuition and the atypical by conscious knowledge has an obvious limit for the layperson. It is restricted to what they can observe in their everyday life, at the human scale. How the physical world behaves at non-human scales (too small or too fast or too heavy) comes within the purview of experts armed with technology, theory, and mathematics. In “The Speed Of Light” I provided a peek into the world of things that are too fast, and the associated counter-intuitive phenomena of clocks slowing down, lengths becoming shorter, and so on. In this article, I tackle the world of things that are too small. Buckle up for a ride outside the world of your intuition.

A Rapid Primer

The theory that describes the too-small world is quantum physics. In fact, this theory also describes the everyday world at the human scale. But it turns out that any quantum effects are imperceptible at the human scale and it’s more useful to instead use classical physics to explain and predict most things you observe with your senses. The history, philosophy, and interpretation of quantum physics are fascinating in their own right. However, such they are not salient for this article, which aims to guide a layperson through some of the counter-intuitive and profound effects of the too-small world. So, I’ll provide a minimal primer on the factual assertions of quantum physics, just enough to be able to understand the emergent phenomena and sidestep any theoretical discussion of the theory itself.

A particle’s state in quantum physics is represented by a wave function defined over space and time: Ψ(x, t). This is analogous to how in classical physics a particle’s position function is defined over time: x(t). The classical particle’s position function must satisfy Newton’s second law. Similarly, the quantum wave function is a solution to Schrodinger’s equation. The wave function determines the particle’s position, momentum, energy, and other such measurable properties, just like the position function determines those for a classical particle. However, unlike a classical particle, the result of a measurement (e.g. the particle’s energy) can be predicted sharply only if the wave function is in a special state associated with the measurable property (e.g. the specific wave function associated with fixed energy). For a general wave function, the prediction is fuzzy: only the probability of measuring a certain value can be predicted. Once a measurement is made, the wave function is said to collapse into the special state associated with that measured value.

Figure 1 below lays out these concepts in more mathematical detail. I’ve presented it here for those of you who may already have some familiarity with quantum physics. For the rest of you, feel free to focus instead on the more qualitative presentation of quantum effects.

A Particle In A Box

Let’s start our journey into the too-small with the simplest of examples: a particle in a box. If you place a particle in a box, you expect it to stay still in the box. If you nudge it, you expect it to start moving at a certain speed. You expect this speed to be anything in a continuous range of reasonable speeds, depending on the magnitude of the nudge. You expect to be able to know at all times exactly where the particle is, in which direction it’s moving, and how fast it’s moving (ignoring energy loss due to friction or bouncing off the walls). Lest your intuition deceives you, you can even carefully work out the details using classical physics, and formulate the particle’s position as a function of time: x(t).

All these expectations are, in fact, wrong. Or rather, they are just convenient approximations to the underlying theory of quantum physics. They merely appear to be true because the corrections to them are too small to be noticeable at the human scale. But if you shrink down below the microscopic scale, you will see the full glory of a particle in a box. Let’s go down there.

What is the quantum wave function for a particle in a one-dimensional box? The particle can move freely inside the box, with no potential affecting it. So the general solution to Schrodinger’s equation for a free particle (listed in Figure 1 above) should apply for 0 ≤ x ≤ L. And, since the particle is constrained inside the box, the probability of finding it outside the box must be 0. This requires the wave function to be 0 outside the box. In particular, the wave function must be 0 at the boundaries of the box (x = 0 and L). Finally, the probability of finding the particle within the box must be 1, which fixes the normalization constant i.e. the constant factor that is allowed to multiply a wave function that satisfies Schrodinger’s equation. Here’s the calculation based on the above constraints:

What are the quantum effects revealed from the wave function calculated above for a particle in a box?

Quantum effect #1: the particle’s energy is quantized.

You can’t really nudge a confined particle to take on any specific speed in a continuum of reasonable speeds. Instead, the allowable speeds take on discrete values (as shown in the boxed equation for Eₙ in the calculation above). This is exactly where the term “quantum” in quantum physics comes from.

So how come you don’t notice this quantization of speeds in your everyday life? Because the gap between the allowable speeds is too small to easily discern. For example, if the particle weighs 1 gram and is placed in a box of size 1 meter, the gap between allowable speeds is ~10⁻³¹ m/s, making it seem as if the speed takes on values in a continuum.

If you can’t easily notice this quantization of energy, why should you care? Because such quantum effects are fundamental to how things work at the atomic and subatomic scales. For example, an atom is in discrete energy states, as explained by quantum physics. When it transitions between two energy levels it absorbs (if transitioning to a higher level) or emits (if transitioning to a lower level) light of a specific color that corresponds precisely to the difference between the energy levels. Astronomers can observe these discrete spectral lines when viewing distant stars and determine exactly what they are made of.

Quantum effect #2: the particle’s lowest possible energy is > 0.

You can’t really place a particle at rest in a box. Even an apparently stationary particle must have a minimal amount of energy, and hence, speed.

So how come you observe stationary things all the time? Because the lowest speed is too small to easily make out at the human scale. A 1 gram particle in a 1 meter box will have a lowest possible speed that would take it 10²⁰ years to move a distance of 1 millimeter! That is 10 orders of magnitude longer than the age of the universe (~10¹⁰ years)!

How does this non-zero lowest allowable energy manifest itself? In a very critical way. Without it, atoms would not be stable, and matter as we know it would not exist. You see, in classical physics, an electron orbiting the nucleus of an atom should radiate away its energy and collapse into the nucleus. However, once the quantum effect of the lowest possible energy is accounted for, the atom can be in a stable state in which the electron is at its lowest energy level (> 0).

Quantum effect #3: the particle’s position and momentum cannot be known simultaneously.

Consider an ensemble of particle-in-a-box systems, with each one in the nth energy state wave function Ψₙ. Since position measurements are fuzzy for a wave function that is not in a sharp position state, you will measure a different position in each system of the ensemble (even if all the measurements are done at exactly the same time). The measured values form a distribution whose standard deviation denotes the amount of uncertainty in the position. Similarly, you can measure the momentum of the particle in each system of the ensemble and determine the uncertainty in the momentum. Turns out that the product of the uncertainty in position and momentum is always larger than a fixed amount expressed in terms of Planck’s constant ‘h’. Here’s a sketch of the calculation:

The more precisely you measure the position of the particle, the more uncertainty you have about its momentum. Conversely, the more precisely you measure the momentum of the particle, the more uncertainty you have about its position. There are other pairs of observables for which similar uncertainty relations hold. Such observables are considered incompatible. Not all observables are incompatible, mind you. For example, you can indeed simultaneously measure the precise momentum and the precise energy of a particle.

Once again, you don’t notice this uncertainty in your everyday experience because the magnitude of the uncertainty is so small. But this uncertainty manifests itself in experiments. For example, gravitational wave detectors rely on minute perturbations to the interference pattern between two beams of light and such sensitive measurements have to contend with the inherent uncertainty between simultaneously measuring the amplitude and phase of the light beams.

Breaking Barriers

Let’s continue our too-small-world journey with another illuminating example: a particle moving towards a barrier. Think of a barrier as a region in space where the particle has to pay a fixed amount of its energy to enter, which it reclaims when it exits. If this notion of a barrier seems contrived, rest assured that it is quite ubiquitously real (e.g. charged particles in electric fields).

What do you expect when a particle approaches such a barrier? If the particle has lower energy than the barrier, you expect it to bounce back from the barrier, unable to pay the price of entry.

On the other hand, if the particle has higher energy than the barrier, you expect it to enter the barrier with a correspondingly decreased speed, and then exit the barrier on the other side, with a kick restoring it to its original speed.

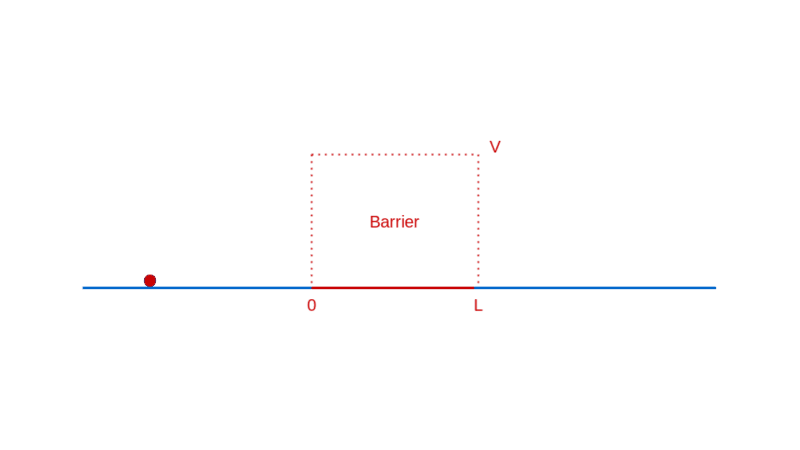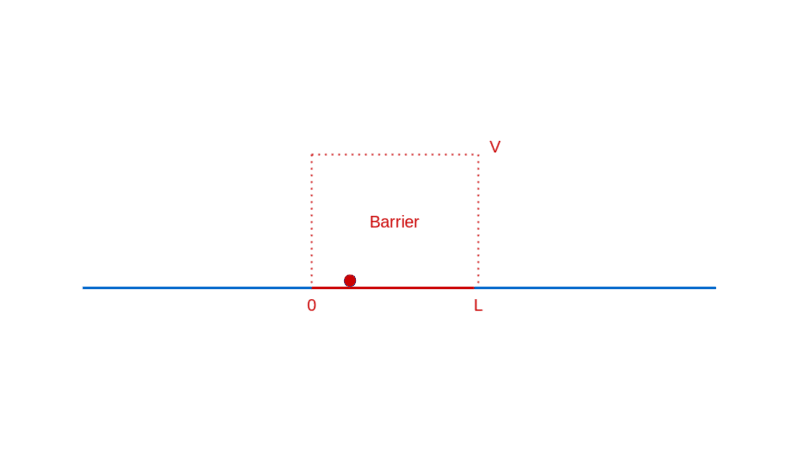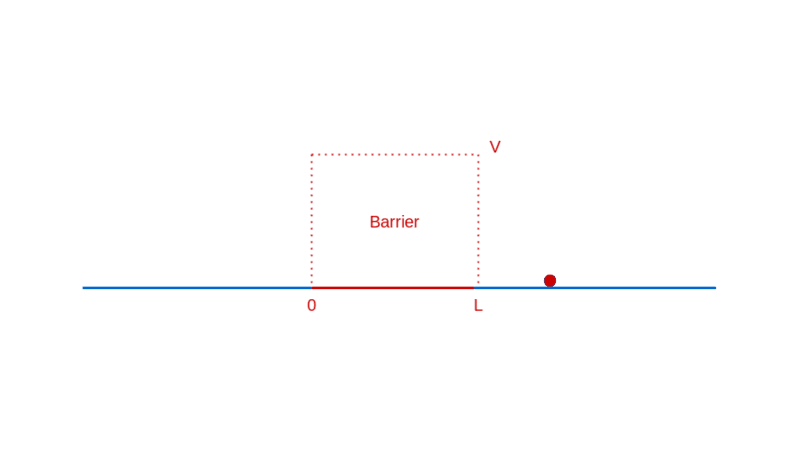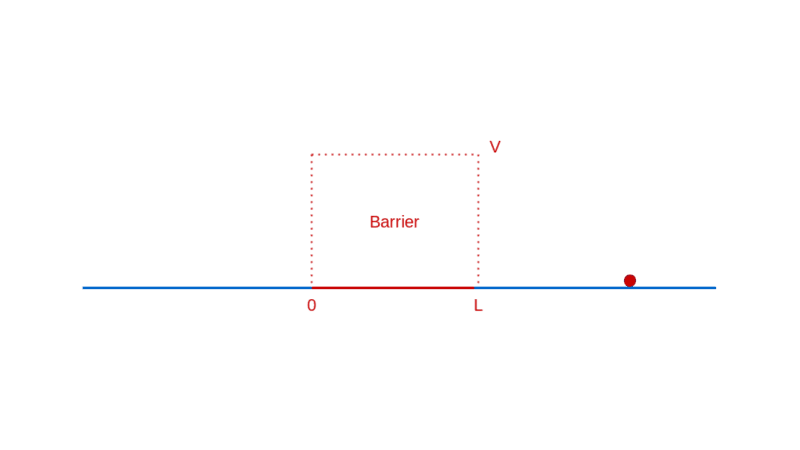
How does quantum physics affect these expectations? To answer that, like before, you have to determine the wave function of the particle. In the region before the barrier, the wave function will comprise a part that denotes the particle moving towards the barrier (the incident part) and a part that denotes the particle reflected off the barrier. In the region after the barrier, the wave function denotes the transmitted particle moving away from the barrier on the other side. Recall that |Ψ(x)|² denotes the probability density of finding the particle at x. So, the amplitude of the transmitted wave function, compared to the amplitude of the incident wave function, provides the probability of the particle breaking through the barrier. Here’s a sketch of the calculation:

And voila, we have:

Quantum effect #4: a particle with energy less than a barrier’s energy has a non-zero probability of tunneling through the barrier.

Let’s explore that in a little more detail to have a clearer mental model of under which conditions such tunneling is significant. How does the tunneling probability change with the width of the barrier, the height of the barrier, and the energy of the particle compared to the barrier?

As the barrier becomes thinner, the particle has a higher likelihood of tunneling through the barrier (despite not having sufficient energy). This is significant in practical ways. For example, it puts a theoretical lower bound on how small an electronic component like a transistor can be without allowing the electrons in the component to tunnel out.

As the barrier becomes lower, the particle has a higher probability of penetrating it (despite not having sufficient energy). Surprisingly, as the barrier approaches the same energy as the particle’s energy, the probability does not quite approach 1. A particle with sufficient energy to penetrate the barrier is not guaranteed to actually do so!

As the particle becomes more energetic, it becomes more likely to tunnel through the barrier (despite still having lower energy than the barrier’s). What happens when the particle has greater energy than that needed to cross the barrier? Naively you would expect such a particle to always go through. In the quantum world, not so.

You don’t notice the unexpected barrier penetration when a particle is lacking in energy, nor the unexpected lack of penetration when a particle has sufficient energy because the effects are only noticeable at small scales. At our everyday scales the tunneling probability is vanishingly small:

Why then should you care about this effect of quantum tunneling? Well, without it the Sun wouldn’t shine. You see, the Sun is powered by nuclear fusion: hydrogen nuclei fuse into helium nuclei and release energy in the process. And, for the positively charged nuclei to fuse they have to overcome the electrostatic repulsion between them. However, the Sun is not hot enough to provide enough energy for the nuclei to fuse. What saves the world, quite literally, is that the nuclei can quantum tunnel through the electrostatic repulsion barrier and fuse with other nuclei.

Fearing Heights

Let’s close with an amusing quantum effect that is perhaps more of a quirk than something more fundamental about how nature works. What happens when instead of a barrier, a particle confronts a “ditch” i.e. a region in space which gives energy to an entering particle and then reclaims that energy back when the particle exits?

You expect a particle to always enter the ditch, get a speed boost, and then return to its original speed when it exits the ditch. But by now you’re probably prepared for quantum effects to belie such expectations. The calculation is exactly the same as that for a barrier, except that the barrier height V should be replaced by the ditch depth -V.

Quantum effect #5: a particle is not guaranteed to cross a ditch. In fact, it is guaranteed to bounce back from an infinitely deep ditch.

Again this quantum effect of a particle eschewing a ditch is only noticeable at small scales and is imperceptible at your everyday human scale. And, to the best of my knowledge, there is nothing deep in nature that is explained by this. Still, it’s an oddity worth noting while we’re marveling at quantum effects.

Summary

That concludes our brief journey into the world of the too-small and the quantum effects therein. Here’s a recap of what we saw:

1. There are counter-intuitive quantum effects that manifest themselves at subatomic scales but are imperceptible at the everyday human scale.
2. One such effect is that a confined particle is allowed to have energy only from among a discrete set of allowable energies rather than a continuum of energies. The gaps between the allowable energies manifest themselves in phenomena like spectral lines that reveal the composition of distant stars.
3. A related quantum effect is that a confined particle’s lowest possible energy is strictly greater than 0. This is fundamental for the existence of matter, otherwise, an atom could not exist due to its electrons radiating away their energy and collapsing into the nucleus.
4. A third quantum effect is that certain properties of a particle (e.g. position and momentum) cannot be simultaneously measured precisely. This uncertainty in the precision of incompatible observables must be contended with in high-sensitivity detectors such as interferometers for gravitational waves.
5. Another quantum effect is that a particle with insufficient energy to penetrate a barrier can nevertheless tunnel through. The probability of tunneling increases as the barrier gets thinner or lower. This effect is critical for us to exist. For example, it enables hydrogen nuclei in the Sun to overcome the electrostatic barrier and fuse into helium to power the Sun.
6. A corollary to quantum tunneling is the amusing curiosity of the tongue-in-cheek named fear-of-heights, in which a particle reflects off an infinitely deep ditch instead of plowing through.