A Geometric Intuition for Energy Conservation

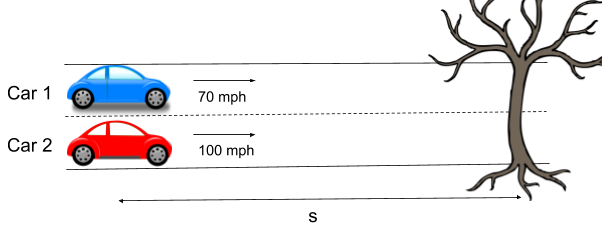
I watched a Numberphile video a while back that posed a problem about decelerating cars that has a surprising and scary answer. Two cars are exactly side by side on a multi-lane road when their drivers break to avoid an obstacle coming up and both cars decelerate at exactly the same constant rate. One car is traveling at 70 mph and manages to stop just before the obstacle. The other car is traveling at 100 mph. What speed does the second car hit the obstacle at?

The answer seems as if it should be 30 mph. While it is true that the second car would have reached 30 mph at the same time that the first car stops, the second car will have already encountered the tree before this time and it does so at the very scary speed of 71 mph.

The video came to this answer by assuming the formula for kinetic energy. A night later, I was trying to get back to sleep after a nocturnal trip to the loo. Instead of counting sheep, I started mulling over whether basic geometry could be used to visualize things without any need for this assumption. So here goes.

Let’s start with a single car accelerating from speed u to v and plot speed against time for a constant acceleration.

The slope or gradient of the bold line is height divided by width or: (v-u)/t. This slope is also speed divided by time which is rate of change of speed also called acceleration- a. So we have: a =(v-u)/t or rearranging:

The second thing we can do is look at the area under the line. The plot is Speed against Time so the area under the line will be Speed multiplied by Time. Speed is distance divided by time so this reduces to distance: s.

This area can be worked out as the sum of the areas of a rectangle (width by height) and a triangle (half width by height):

This comes to: s=(t) (u) +½(t) (at) which reduces to:

We have two nice equations involving time but alas, as the problem was posed, we have no information about time.

What other information do we have besides the starting speeds of the cars? Basically only this- they both decelerate at the same rate and travel the same distance to the obstacle where one manages to stop and the other collides.

As a shot in the dark, let’s see what happens if we square v:

Let’s split the top right square diagonally to make two triangles.

Now we have a triangle on top of a square which should remind us of a similar diagram we had before.

Or in the language of algebra: uat+½a²t²=a(ut+½at²)=as

Putting this back in our square, v² now looks like this:

Which gives us a nice equation with no t’s:

Now we have everything we need to solve the original problem. (Here we’re decelerating so u is greater than v.)

The acceleration- a (actually deceleration in this case) is the same for car 1 and car 2 and so is the distance traveled- s. This means that the blue area is the same for both cars.

U₁²=2as and U₂²=2as+V₂²

So putting it all together we get: U₂²=V₁²+U₁² which we can represent as the side lengths in a right angled triangle:

Which works out as: V₁²= U₂²-U₁²= 100²–70²= 5100 and taking the square root we get a very painful final speed of 71 mph.

Interestingly no physics was needed for this- just math. I suppose this means that these equations will hold in all possible universes or at least those that have objects that can be given a constant acceleration by some mechanism.

However let’s go one step further and see if we can derive the formula for kinetic energy that was assumed in the Numberphile video.

Firstly, if we chop our square diagonally, we notice something interesting that I will henceforth call a half speed squared triangle or speed triangle for short:

We now have the following equation:

If we multiply across by m for mass, we get the following:½mu²+mas=½mv²

This turns out to be what is recognized in physics as the law of conservation of mechanical energy:

Initial Kinetic Energy + Potential Energy= Final Kinetic Energy

This is too much of a coincidence to have happened by accident but how does it come about? To gain a better appreciation, let’s turn everything around from a car decelerating horizontally to an object accelerating vertically from an initial height.

Imagine the object is released at speed 0 and falls to the ground by which time it has reached speed v. If it has a perfectly elastic collision with the ground (perhaps a trampoline would be better than grass), then it will immediately gain a speed of -v in the opposite direction, rise to the same height h at speed 0 and then start falling again to repeat the cycle all over again. Moreover if we were to video this behavior and play it back we would be unable to tell whether the video was being played forwards or backwards. This is a time symmetry and the great Emmy Noether proved that wherever there is a symmetry, there is an associated conservation law.

In our universe, anything that is unsupported near a large body falls to the ground with a constant acceleration regardless of its mass or at least it does if we can ignore air resistance. This was demonstrated in the best show-and-tell ever using a hammer and a feather on the moon by Commander David Scott of Apollo 15:

This is often regarded as being due to the equivalence principal. However rather than considering gravitational and inertial mass as equal just to cancel them, we can simply ignore mass as irrelevant, at least for now.

On earth where the constant acceleration is six times the moon’s: a=9.8 m/s² or 32 ft/s², let’s release an object above the ground at height h.(To keep things simple, we are going to count time backwards from 0 where it hits the ground.)

We are guaranteed that by the time it has reached the ground, the object will have experienced an acceleration a over a distance h. It it then bounces elastically, it will eventually gain the same but only by loosing all it’s speed.

Thus, we can regard this “energy” as being in the bank or potential “energy” = ah- the area of the triangle. (Here “energy” is in quotes because it’s a working definition that so far does not involve mass) As the object falls, the potential “energy” reduces and the speed of the object increases until the object is going at v just before it hits the ground. We might as well call this kinetic “energy” and we know that it is equal to ½v². At any time in between release and ground collision, it will be traveling at an intermediate speed of u at a height s above the ground. According to equation 4, we have:

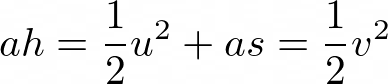
As ah and ½v² are both just the area of the triangle which doesn’t change this can be rephrased as:

Which amounts to: Kinetic “Energy” +Potential “Energy”=Constant

This looks like an impressive conservation law but it’s nothing more complicated than the mathematical fact that the total area of a triangle does not change if it is split into two pieces.

So far, we’ve gotten away without worrying about mass. However let’s experiment with our potential “energy” using a pulley system where the acceleration field is ”a” as before.

We find that with the gentlest of pulls, we can use weight 2 to raise weight 1. This is exactly what we would expect if our potential “energy” is conserved.

Beforehand, weight 2 has potential “energy” ah and weight 1 has potential “energy” 0 and afterwards the situation is reversed.

However if we experiment with different weights, we find the following::

In order to move weight 1 with negligible effort, we need a more complicated pulley system and this only raises weight 1 by ½h by the time weight 2 has reached the ground. (This is a version of Archimedes’ law of the lever.)

In order for potential “energy” to be conserved in this situation, we need to modify our definition by including mass: Potential Energy=mah

With this new definition, equation 6 can still hold if we multiply across by m which is also a constant at speeds well below the speed of light:

Now that we have our final definition, we can get rid of the quotes around energy: Kinetic Energy + Potential Energy = Constant . And it turns out in our universe that conservation doesn’t just apply to mechanical energy. If we come up with appropriate definitions for chemical energy, nuclear energy and so on, we can sum them all up to a constant for a closed system.

Let’s finish by updating our velocity triangle to an energy triangle by including mass m:

We now have the more usual definition of kinetic energy as ½mu² but if we use Newton’s definition for force (from his second law of motion) of F=ma, the area of the blue triangle gives us:

Potential Energy = Energy Transferred = Force times Distance

“Energy transferred” is sometimes called Work which is why you often see variations of the following sentence:

“When a force moves its point of application through a distance in the direction of the force, work is said to be done.”

The energy triangle also introduces momentum p which turns out to be conserved in all collisions whether or not they are elastic — but exploring that will have to wait for another time.

So the next time a physicist friend tries to impress you with fancy-schmancy concepts like conservation of energy and Newton’s second law of motion, you can (somewhat unfairly) take them down a peg by telling them it’s mostly just down to the fact that cutting a triangle in two does not affect its total area.