Arguably the most important unsolved problem in pure mathematics today is to prove (or disprove) the Riemann hypothesis, which is intimately connected to the distribution of prime numbers. One of the basic techniques needed to understand the problem is called analytic continuation, which is the topic of this article. Analytic continuation is a technique from a branch of mathematics called complex analysis used to extend the domain over which a complex analytic function is defined.

Some Important Mathematical Concepts

Before introducing the technique, I will briefly explain some important mathematical concepts that will be needed.

Taylor Series

Suppose we want to find a polynomial approximation to some function f(x). A polynomial is a mathematical expression formed by variables and coefficients. They involve the basic operations (addition, subtraction, and multiplication) and contain only non-negative integer exponents of the variables. A polynomial in one variable x of degree n can be written as:

Now suppose the polynomial has an infinite degree (it is given by an infinite sum of terms). Such polynomials are called Taylor series (or Taylor expansions). Taylor series are polynomial representations of functions as infinite sums of terms. Each term of the series is evaluated from the values of the derivatives of f(x) at one single point (around which the series is centered). Formally a Taylor series around some number a is given by:

where the upper indices (0), (1), … indicate the order of the derivative of f(x) as x=a. One can approximate a function using a polynomial with only a finite number of terms of the corresponding Taylor series. Such polynomials are called Taylor polynomials. In the figure below, several Taylor polynomials for the function f(x) = sin x with an increasing number of terms (hence, increasing degrees) are shown.

The first four Taylor polynomials for f(x) = sin x are given by:

Convergence

The concept of convergence of infinite series will also be crucial in our discussion of the analytic continuation. A mathematical sequence is a list of elements (or objects) with a particular order. They can be represented as follows:

A well-known example of a sequence is the Fibonacci sequence0,1,1,2,3,5,8,13,21,34,55,… where each number is the sum of the two preceding ones.

One builds a series by taking partial sums of the elements of a sequence. The series of partial sums can be represented by:

where:

An example of a series, the familiar geometric series, is shown below. In a geometric series, the common ratio between successive elements is constant. For a ratio equal to 1/2 we have:

Fig. 5 shows pictorially that the geometric series above converges to twice the area of the largest square.

A series such as in Eq. 6 is convergent if the sequence Eq. 5 of partial sums approaches some finite limit. Otherwise, the series is said to be divergent. An example of a convergent series is the geometric series in Eq. 7. An example of a divergent series is:

It is easy to see that the harmonic series diverges by comparing it with the integral of the curve y=1/x. See Fig.6. Since the area below the curve is entirely contained within the rectangles and the area below y=1/x is:

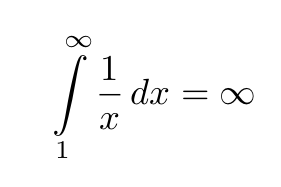
the total area of the rectangles must be infinite as well.

The geometric series is, in general, the sum of successive powers of a given variable x (see Fig. 5). More concretely, consider the following geometric series where the first term is 1 and the common ratio is x:

To find a closed form for this sum is not difficult. Just multiply both sides by x

and subtract both equations. Most terms cancel out and we are left with:

If |x|<1 and we take x→ ∞, the first term in the numerator of the sum goes to zero and we obtain:

In contrast to Eq. 12, this power series is not valid for any x but has an interval of convergence (see figure below), namely |x|<1.

Now let’s see what happens when we set x=2, which is outside the interval of convergence of the series Eq. 13. We obtain:

We obtain an arithmetically invalid sum. This shows again that associating a function with the infinite series Eq. 13 only holds for a limited range of the variable x.

Complex Numbers: Analytic Functions, Poles and Convergence Discs

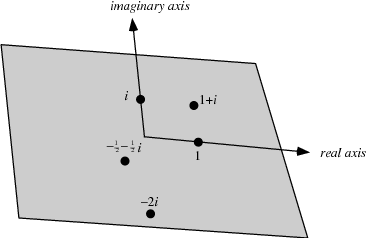
Until now, our analysis was restricted to real numbers. Now we will extend it to complex numbers. The complex plane is a geometric representation of the complex numbers, as shown in Fig 7.

Let us consider an expansion of an analytic complex function f(z). By definition, an analytic function is a function locally given by a convergent power series. If f(z) is analytic at z₀, the power series reads:

In analogy with the case of the geometric series, where convergence was restricted to an interval with radius 1 on the real line, this series will converge only over a circular region of the complex plane centered on the complex number z₀.

The convergence region of f(z) is a circular region centered on z₀ extending to the closest pole, where f(z) goes to infinity. Fig. 9 shows the convergence region (bounded by the white circle) of the function 1/(1+z²).

Another example of a complex function containing poles is the absolute value of the Gamma function|Γ(z)| shown in Fig.10. The Gamma function is given by:

The figure shows examples of two points where |Γ(z)| becomes infinite due to the presence of poles. Eventually, as one goes to the right, the function does not exhibit more poles, and it only increases.

A stronger criterion of convergence is called absolute convergence. We call the convergence we already discussed conditional convergence. Absolute convergence occurs when the following series converges:

When a series is absolutely convergent it is also conditionally convergent. There are a few tests of absolute convergence, one of them is the ratio test. Consider the series:

Now define the following ratio:

The series Eq. 18 converges absolutely if r<1 and diverges if r>1. If r=1, no conclusion can be taken.

It is straightforward to apply the ratio test (or any other convergence test) to show the following important result:

Let us now finally investigate the technique of analytic continuation, which is the main topic of this article!

Analytic Continuation

We already know, from the introduction, that analytic continuation is a technique to extend the domain of an analytic function. We can now be more formal and define it as follows. Suppose f(z) is analytical on a region R. Now suppose that R is contained in a region S. The function f(z) can be analytically continued from R to S if there exists a function g(z) such that:

• g(z) is analytic on S
• g(z)=f(z) for all z ∈ R

Another important property of the analytic continuation procedure is that it is unique (see these notes for more details).

An example will make this definition clearer (this section was based mostly based on this analysis). We start with the expansion of the function

which has a pole at z=1. The corresponding convergence disk is shown in the figure below:

We can expand the function given by Eq. 21 about any point where the function and its derivatives are well-behaved. For example, let z₀=2. To expand the series around it we need to evaluate the derivatives of f(z) at z₀=2. The derivatives are:

We now insert these derivatives in the power series Eq. 15 to get:

Substituting z₀=2 we get:

Suppose that we do not know the closed-form expression for some function f(z) but we know only its power series in some region of the complex plane. Let such power series be

We already saw that this series is convergent only for complex numbers with magnitudes smaller than 1. Let us see how to determine the value of this function at any z (except for the pole at z=1) using analytic continuation. To do that, consider Fig. 14 below:

We can calculate the function f(z) and its derivatives at any point within the convergence disc |z|<1. Hence, we can choose some point such as z₀ (shown in the figure), and determine the power series for f(z+z₀). This power series will be convergent within a circular disc centered on z₀, extending to the closest pole at z=1 (see Fig. 14). We conclude, therefore, that we can evaluate the function at complex values outside the convergence region of the original power series.

The next step is self-evident. See Fig. 14. Once we have evaluated the power series for f(z+z₀), we can use the same procedure and select another point z₁ that lies inside the new region of convergence. We then determine the power series expansion for f(z+z₁), which will converge within the new circular region centered on z₁ (which, as before, extends to the closest pole z = 1).

Continuing this procedure, one can analytically extend the function through the full complex plane excluding the poles of the function!

An Application of Analytic Continuation: The Riemann Hypothesis

Georg Friedrich Bernhard Riemann was a German mathematician considered by many to be one of the greatest mathematicians of all time. He contributed to a multitude of branches of mathematics and physics (his work on differential geometry set the foundations of Einstein’s theory of general relativity). One of the applications of analytic continuation is on his work on prime numbers, more specifically, his 1859 paper containing the first statement of the now-famous Riemann hypothesis.

The Riemann zeta function is the following function of the complex s, defined on the right side of the vertical line Re(s)=1 in the complex plane by the absolutely convergent infinite series

and in the rest of the complex plane via analytic continuation. To see why the series above is valid only for Re(s)>1 we take the absolute value of a generic term

As we saw before, an infinite series is absolutely convergent if the sum of the absolute values of the summands (the elements of the sum) is finite. Hence, for Eq. 26 to converge absolutely, we must have Re(s)>1. Riemann showed that by analytic continuation one can extend ζ(s) to the whole complex plane (with only a pole at s=1).

The Riemann hypothesis states that:

The real part of every non-trivial zero of the Riemann zeta function is 1/2.

The figure below illustrates the hypothesis. It shows the following important objects:

• The so-called trivial zeros -2, -4, -6,…
• The critical strip which contains all non-trivial zeros of ζ(s)
• The critical line which, if the hypothesis is true, contains all non-trivial zeros

My Github and personal website www.marcotavora.me have some other interesting material both about mathematics and other topics such as physics, data science, and finance. Check them out!