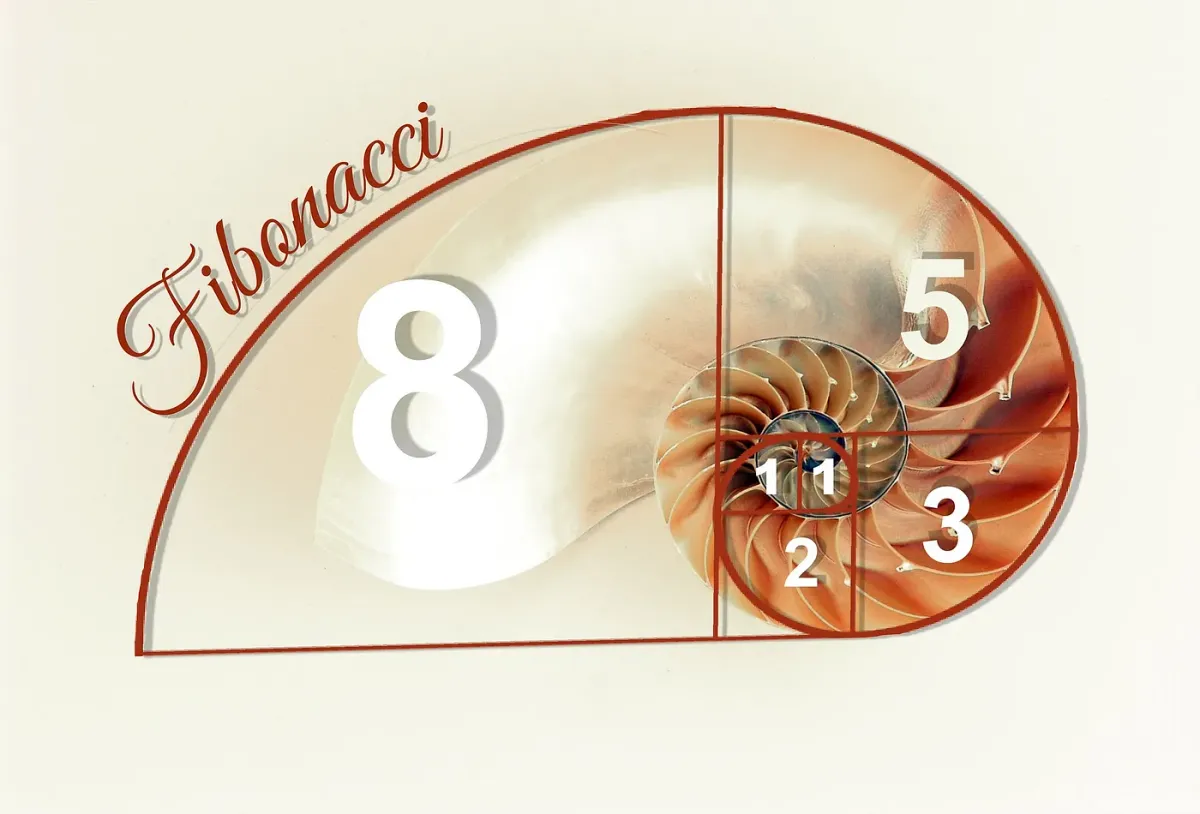
Fibonacci numbers are one of the most captivating things in mathematics. They hold a special place in almost every mathematician’s heart. Throughout history, people have done a lot of research around these numbers, and as a result, quite a lot of interesting facts have been discovered.

Let us see how they look like -

Any number in this sequence is the sum of the previous two numbers, and this pattern is mathematically written as

where n is a positive integer greater than 1, Fₙ is the n−th Fibonacci number with F₀=0 and F₁=1.

Now, this expression is fairly easy to understand and quite sufficient to produce any Fibonacci number by plugging the required value of n. If at all, its only drawback is that, if we want to know a particular number, Fₙ​ in the sequence, we need two numbers Fₙ₋₁ and Fₙ₋₂​ that came before it; that’s just how this formula works. It is not hard to imagine that if we need a number that is far ahead into the sequence, we will have to do a lot of “back” calculations, which might be tedious.

In this article, we are going to discuss another formula to obtain any Fibonacci number in the sequence, which is (arguably) easier to work with.

The Formula

Let us define a function F(x), such that it can be expanded in a power series like this

Here we have omitted F₀, because F₀=0, by definition.

(Issues regarding the convergence and uniqueness of the series are beyond the scope of the article)

Our job is to find an explicit form of the function, F(x), such that the coefficients, Fₙ​ are the Fibonacci numbers.

In order to make use of this function, first we have to rearrange the original formula. If we make the replacement

the original formula becomes

It is easy to check that this modification still produces the same sequence of numbers, starting from n=1, instead of n=0.

Next, we multiply the last equation by xⁿ to get

and perform a summation over n to get

Let us first consider the left hand side of this equation —

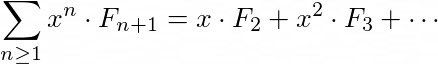
Now, we try to represent this expansion in terms of F(x), by doing the following simple manipulations -

• Multiply and divide by x to get

• Add and subtract x ⋅ F₁​ to get

Using the definition of F(x), this expression can now be written as

Therefore, using the fact that F₁=1, we can write the entire left hand side as

Let us now consider the right hand side —

If we expand these two terms, we get

We have again omitted F₀, because F₀=0.

By taking out a factor of x from the second expansion, we get

Using the definition of F(x), this can finally be written as

Therefore, by equating the left and the right hand sides, the original formula can be re-written in terms of F(x) as,

Let us now simplify this expression a bit more. The denominator is a quadratic equation whose roots can easily be obtained to be

(For an easy graphical method of finding roots, check out this article)

Using these roots, it is possible to write the denominator as

so that we can write

We can split the denominator and write this as

Before we proceed, we need to understand a useful fact about geometric series. If we have an infinite series

with |ax| < 1, then its sum is given by

This means, if the sum of an infinite geometric series is finite, we can always have the following equality -

Using this idea, we can write the expression of F(x) as

The factor of 1/√5 is due to the substitution of α and β.

Recalling the original definition of F(x), we can finally write the following equality

and by comparing the n−th terms on both sides, we get a nice result

with

(The number α is also a very interesting object in itself. It goes by the name of golden ratio, which deserves its own separate article.)

We can see from the following table, that by plugging the values of n, we can directly find all Fibonacci numbers!

This article was originally published at physicsgarage.